手动开平方的一种方法
算法步奏:
1)将给定的需要数两位一段分成若干段,个位、十位作为一段,其他往左往右两位一段;
2)求平方根的最左位,取分段的最左段作为被减数,依次将1、3、7、9、11、13…作为减数,直到减到最小非负为止;
3)求平方根的第二位,将上一步减法最后一次减法的余数r作为此轮被减数的左半部分,右半部分是第二段的两位数ab,即被减数为rab;上一轮最后一次减法的减数+1得到c作为此轮减数的左半部分,右半部分为1、3、5、7、9、11…,即减数为c1、c3、c5、c7、…,直至减到最小非负为止;
4)重复步骤3),求平方根的下一位;
5)当得到的余数为0或所有段处理完时计算结束。
例子:对80315.56开平方运算
第一步:将所给数分段,个位、十位(如果有的话)作为一段;再依次往左往右每两位作为一段。80315.56被分成四段,8、03、15、56,再按以下规则施行一系列减法依次确定所给数平方根的每一位;
第二步:确定平方根的最左位,此例的最左段为8,将其作为被减数,依次用减数1、3、5、7、9、11、13、15、17…来减它。8-1=7,7-3=4,再往下4-5已无法进行,故此轮能有效施行的减法运算次数仅为2,从而确定80315.56的平方根的最左位是2;
第三步:确定平方根的第二位(靠左),将上一步减法最后余数(4)添上下一段两位数(03)构成本轮的被减数(即403),而减数的结构由上一轮有效施行的减法的最后一次的减数(3)加上1(得4)作为本轮减数的最左位,减数的右半部分依次由1(得41)、3(得43)、5(得45)、7(得47)、9(得49)、11(得51)…构成。于是有以下减法运算:403-41=362、362-43=319、319-45=274、274-47=227、227-49=178、178-51=127、127-53=74、74-55=19,至此再往下已无法进行,此轮有效施行了8次减法,可确定平方根第二位为8;
第四步:确定下一位,将上一步减法最后余数(19)添入下一段两位数(15)构成本轮被减数1915;而减数由上一轮最后一次减法的减数55加一(56)构成最左位,右部分由1、3、5、7、9、11、…构成,于是有如下减法运算:1915-561=1354、1354-563=791、791-565=226,已无法往下运算,此轮有效减法为3次,所以确定平方根此位为3;
第五步:确定下一位,将上一步减法最后余数(226)添到下一段两位数(56)构成本轮被减数22656;而减数由上一轮最后一次减法的减数565加1(566)作为其最左位,右部分由1、3、5、7、9、11…构成。于是有如下运算:22656-5661=20995、20995-5663=15332、15332-5665=5667、5667-5667=0,结束,此轮有效减法4次,可确定平方根此位为4;
第六步:在对应位上添加小数点,得到80315.56的平方根283.4。
Raptor流程图:
① main程序
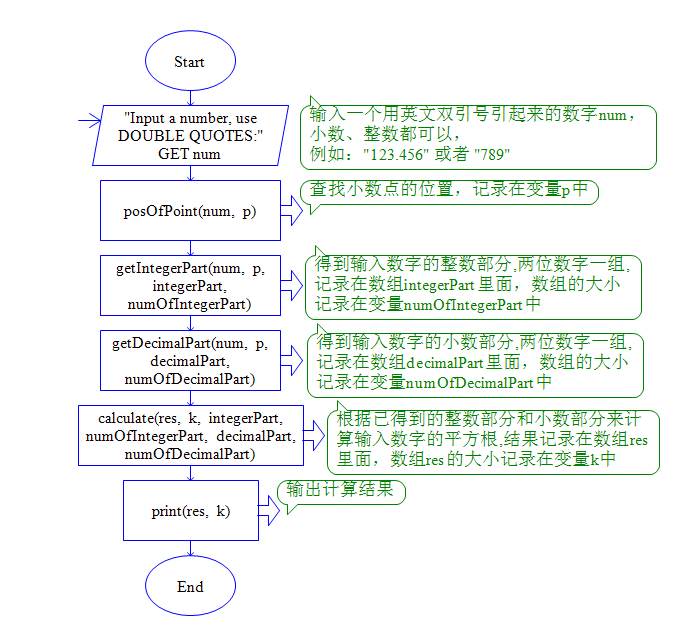
② posOfPoint子程序

③ getIntegerPart子程序

④ getDecimalPart子程序

⑤ strlen子程序

⑥ calculate子程序
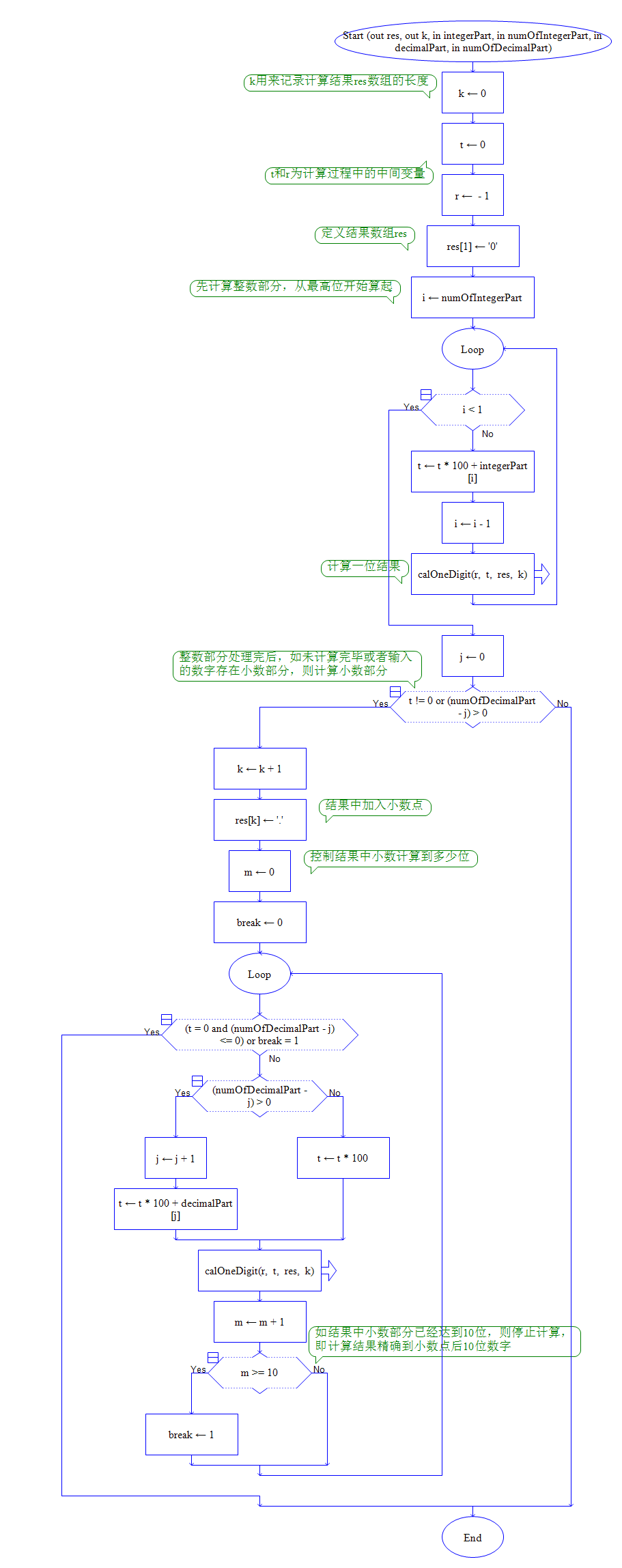
⑦ calOneDigit子程序

⑧ print子程序

C++程序:
1 #include <stack> 2 #include <queue> 3 #include <stdio.h> 4 #include <string.h> 5 #include <math.h> 6 using namespace std; 7 8 stack<int> integerPart; 9 queue<int> decimalPart; 10 void initData(); 11 void posOfPoint(const char num[], int &p); 12 void getIntegerPart(const char num[], const int p); 13 void getDecimalPart(const char num[], const int p); 14 void calculate(char res[], int &k); 15 16 int main() 17 { 18 char num[100]; 19 char res[100]; 20 int p, k, i; 21 22 gets(num); 23 posOfPoint(num, p); 24 getIntegerPart(num, p); 25 getDecimalPart(num, p); 26 calculate(res, k); 27 for(i=0; i<k; i++) 28 printf("%c", res[i]); 29 printf("\n"); 30 31 return 0; 32 } 33 34 void posOfPoint(const char num[], int &p) 35 { 36 for(p=0; num[p]!=0; p++) 37 { 38 if(num[p]=='.') 39 break; 40 } 41 } 42 43 void getIntegerPart(const char num[], const int p) 44 { 45 for(int i=p-1; i>=0; i--) 46 { 47 int t = num[i] - '0'; 48 i -= 1; 49 if(i>=0) 50 t += (num[i] - '0') * 10; 51 integerPart.push(t); 52 } 53 } 54 55 void getDecimalPart(const char num[], const int p) 56 { 57 int len = strlen(num); 58 if(p>=len) 59 return ; 60 61 for(int i=p+1; i<len; i++) 62 { 63 int t = num[i] - '0'; 64 i += 1; 65 if(i<len) 66 t = t * 10 + (num[i] - '0'); 67 else 68 t *= 10; 69 decimalPart.push(t); 70 } 71 } 72 73 void calOneDigit(__int64 &r, __int64 &t, char res[], int &k) 74 { 75 r = (r + 1) * 10; 76 for(int i=0; ; i++) 77 { 78 if(t-(r+2*i+1)>=0) 79 t -= r + 2 * i + 1; 80 else 81 { 82 res[k++] = i + '0'; 83 r = r + 2 * i - 1; 84 break; 85 } 86 } 87 } 88 89 void calculate(char res[], int &k) 90 { 91 __int64 t = 0; 92 __int64 r = -1; 93 k = 0; 94 95 while(!integerPart.empty()) 96 { 97 t = t * 100 + integerPart.top(); 98 integerPart.pop(); 99 calOneDigit(r, t, res, k); 100 } 101 if(t!=0 || !decimalPart.empty()) 102 { 103 res[k++] = '.'; 104 int m = 0; 105 while(t!=0 || !decimalPart.empty()) 106 { 107 if(!decimalPart.empty()) 108 { 109 t = t * 100 + decimalPart.front(); 110 decimalPart.pop(); 111 } 112 else 113 t *= 100; 114 calOneDigit(r, t, res, k); 115 m++; 116 if(m>=15) 117 break; 118 } 119 } 120 }



