The Simplest Course About The Slope Optimization

The Simplest Course About The Slope Optimization

中国人戳这里

As a beginner, I have not understood the Slope Optimization very, this blog is just for who is the same as me who is a beginner.

Buck up a minute.··

I will introduce what i what to say mainly using a classic problem.

Original question

HDU3507

Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

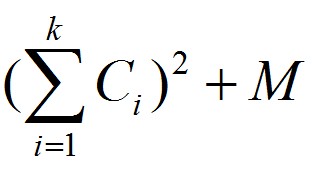
M is a const number.Now Zero want to know the minimum cost in order to arrange the article perfectly. (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000)

The means of the problem

It give you a numerical array a₁~a_n, and you can devide into substrings with the cost of M every substring.

And you should pay the Summation of square of summation of every elements in each substring.

Exactly Resolution

First, think about if there n is less than 5000 instead of 500000, how will you solve this question.

I think you can easily find that the operation is without aftereffect, so you can use dynamic programming.

Define f[i] as the least cost of it when we have already do at the i-th number.

And  we can Pretreatment an array named sum that sum[i] is means the summation of a₁~a_i

The transformation equation is that f[i] = min(f[j] + (sum[i]-sum[j-1])² + M) (j is from 1 to i)

Ok, the normal way to find the j that make that the value of the polynomial least is by going through 1~i

But, you will realize that it will take O(n²) to solve the problem. Apparently, it will break up the time limit of this problem.

Ok, so we should use the slope optimization.

The Slope Optimization

Derivation of formula

We define that k < j < i and we now are finding the f[i].

From the polynomial that I wrote, we can infer that if (sum[i]-sum[k-1])² + f[k] + M < (sum[i]-sum[j-1])² + f[j] + M we must transform the k instead of i;

Then simplify the inequality, we get 

2*sum[i]*(sum[j-1]-sum[k-1]) < f[j]-f[k]+sum[j-1]²-sum[k-1]²

Divide the (sum[j-1]-sum[k-1])

get: 

2*sum[i] < (f[j]-f[k]+sum[j-1]²-sum[k-1]²) / (sum[j-1]-sum[k-1])

The use of slope

You may not be able to find any slope in that formula, but let's try define the g(x) = f[x]+sum[x-1]

And that formula turns to g(j) - g(k) / sum[j-1]-sum[k-1].

Ok, then try to image what it is like, now?

Right, slope.

Ok, create a ectangular coordinate system,

 

 

To find the best point to transform, we will find the line that has slope that just greater  than 2*sum[i]

optimization

Appearently，this way will also break up the time limit.

And, just think, the slope from f[i] to [n] of line that we choose must be monotonically increasing.

So, we can create a convex hull  to find the line.

Right, it's that picture.

But why we can use the convex hull without omiting any answer.

Because all the point between kj and ji, the slope of it will be less than kj or be bigger than ji.

So, it clearly is not be the best choice.

Last use a monotonic queue to maintain the convex hull.

And following is the code.

#include<bits/stdc++.h>
using namespace std;
int a[500101];
int sum[500101];
int que[500101];
int dp[500101];
bool cal(int ax,int ay,int bx,int by,int cx,int cy)
{
    return (ax-bx)*(cy-by)>=(ay-by)*(cx-bx);
}
int gety(int x)
{
    return dp[x-1]+sum[x-1]*sum[x-1];
}
int getx(int x)
{
    return sum[x-1];
}
int get(int i,int ss)
{
    return gety(i)-2*ss*getx(i);
}
int main()
{
    int n,m;
 
    while(scanf("%d%d",&n,&m) != EOF)
    {
    memset(sum,0,sizeof(sum));
    memset(dp,0,sizeof(dp));
    for(int i = 1;i <= n;i++)
    {
        scanf("%d",&a[i]);
        sum[i] = sum[i-1] +  a[i];
    }
    int head = 0,tail = -1;
    for (int i = 1;i <= n;i++)
    {
        while(head < tail && cal(getx(que[tail-1]),gety(que[tail-1]),getx(que[tail]),gety(que[tail]),getx(i),gety(i)))
        {
            tail--;
        }
        que[++tail] = i;
        while(head < tail && get(que[head],sum[i]) >= get(que[head+1],sum[i]))
        {
            head++;
        }  
        dp[i] = get(que[head],sum[i]) + m + sum[i]*sum[i];
    }
    printf("%d\n",dp[n]);
    }
    return 0;  
}