浅谈——RMQ

图论基础知识

感谢：https://www.cnblogs.com/yoke/p/6949838.html

1.RMQ是啥？

摘自百度

其实你不用看，百度的概念有几个看得懂的？

对于长度为n的数列A。
回答若干询问RMQ（A[i,j]）(i,j<=n)，
返回数列A中下标在i，j之间的最小/大值。

 2.有什么方法？

1. 普通遍历查询，O(1)-O(N)
2. 线段树，O(N)-O(logN)
3. DP，O(NlogN)-O(1)
4. RMQ标准算法，O(N)-O(1)

我们这里讲的是DP算法——>ST算法

ST算法是一种比较高效的在线算法。

所谓在线算法，是指用户每输入一个查询便马上处理一个查询。该算法一般用较长的时间做预处理，待信息充足以后便可以用较少的时间回答每个查询。

ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

3.怎么做？

首先是预处理，用动态规划（DP）解决。

设A[i]是要求区间最值的数列，F[i, j]表示从第i个数起连续2^j个数中的最大值。（DP的状态）

例如：

A数列为：3 2 4 5 6 8 1 2 9 7

F[1，0]表示第1个数起，长度为2^0=1的最大值，其实就是3这个数。

同理

F[1,1] = max(3,2) = 3；

F[1，2]=max(3,2,4,5) = 5；

F[1，3] = max(3,2,4,5,6,8,1,2) = 8.

---

并且我们可以容易的看出F[i,0]就等于A[i]。（DP的初始值）

这样，DP的状态、初值都已经有了，剩下的就是状态转移方程。

我们把F[i，j]平均分成两段（因为f[i，j]一定是偶数个数字，2^j）

从 i 到i + 2 ^ (j - 1) - 1为一段；’i + 2 ^ (j - 1)到i + 2 ^ j - 1为一段，长度都为2 ^ (j - 1)。（just 如下图）

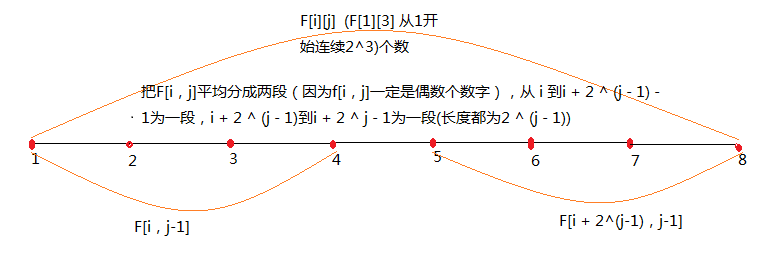
用上例说明，当i=1，j=3时就是3,2,4,5 和 6,8,1,2这两段。F[i，j]就是这两段各自最大值中的最大值。于是我们得到了

状态转移方程 F[i, j]=max(F[i，j-1], F[i + 2^(j-1)，j-1])。

void RMQ(int num) //预处理->O(nlogn)
{
    for(int j = 1; j < 20; ++j)    // 这里j的范围根据具体题目数据定义
        for(int i = 1; i <= num; ++i)    // num为数组内整数的个数
            if(i + (1 << j) - 1 <= num)
            {
                maxsum[i][j] = max(maxsum[i][j - 1], maxsum[i + (1 << (j - 1))][j - 1]);
                minsum[i][j] = min(minsum[i][j - 1], minsum[i + (1 << (j - 1))][j - 1]);
            }
}

这里我们需要注意的是循环的顺序，

我们发现外层是j，内层所i，这是为什么呢？

可以是i在外，j在内吗？

因为我们需要理解这个状态转移方程的意义。
状态转移方程的含义是：先更新所有长度为F[i,0]即1个元素，然后通过2个1个元素的最值，获得所有长度为F[i,1]即2个元素的最值，然后再通过2个2个元素的最值，获得所有长度为F[i,2]即4个元素的最值，以此类推更新所有长度的最值。

而如果是i在外，j在内的话，我们更新的顺序就是F[1,0],F[1,1],F[1,2],F[1,3],表示更新从1开始1个元素，2个元素，4个元素，8个元素（A[0],A[1],....A[7]）的最值，这里F[1,3] = max(max(A[0],A[1],A[2],A[3]),max(A[4],A[5],A[6],A[7]))的值，但是我们根本没有计算max(A[0],A[1],A[2],A[3])和max(A[4],A[5],A[6],A[7])，所以这样的方法肯定是错误的。

为了避免这样的错误，一定要好好理解这个状态转移方程所代表的含义。

如何查询：

假如我们需要查询的区间为(i,j)，那么我们需要找到覆盖这个闭区间(左边界取i，右边界取j)的最小幂

（可以重复，比如查询5，6，7，8，9，我们可以查询5678和6789）。

因为这个区间的长度为j - i + 1,所以我们可以取k=log2( j - i + 1)

则有：RMQ(A[i, j])=max{F[i , k], F[ j - 2 ^ k + 1, k]}。

举例说明，要求区间[2，8]的最大值

k = log2（8 - 2 + 1）= 2

即求max(F[2, 2]，F[8 - 2 ^ 2 + 1, 2]) = max(F[2, 2]，F[5, 2])；

所以最大的k=log2(R-L+1),在程序中可以用log(R-L+1)/log(2)直接计算k。（记得调用cmath库,万能头不就完了）

4.模板练习 

P1816 忠诚

题意：求区间最小值。

#include<cstdio>
#include<string>
#include<cmath>
using namespace std;

const int maxm=1e5+5;
int m,n;
int f[maxm][21];

int read() //快读
{
    int x=0,f=1;char c=getchar();
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void before()//预处理
{
    for(int j=1;j<=20;j++)
    for(int i=1;i<=m;i++)
    {
        if(i+(1<<j)-1<=m)  //未越界
        f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); //dp核心
    }
}

void readdata()
{
    m=read(),n=read();
    for(int i=1;i<=m;i++)
    {
        f[i][0]=read();  //初值
    }
    before();
    for(int i=1;i<=n;i++)
    {
        int a=read(),b=read();
        int k=log(b-a+1)/log(2);  //计算k
        printf("%d ",min(f[a][k],f[b-(1<<k)+1][k])); //计算最大值
    }
}
int main()
{
    readdata();
    return 0;
}

练习：P1886 滑动窗口