浅说——最短路径
四种方法:
Dijkstra,Bellman-ford,SPFA,Floyd

—————————————————————————————————————————————————
思想(懒得看可以不看,就是加离源点最近的边,懂?):
G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合
(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将其加入到集合S中,直到全部顶点都加入到S中,算法就结束了)
第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
形象一点:
我们把点分为两类,一类是已确定最短路径的点,称为“白点”,另一类是未确定最短路径的点,称为“蓝点”。
如果我们要求出一个点的最短路径,就是把这个点由蓝点变为白点。从起点到蓝点的最短路径上的中转点在这个时刻只能是白点。
Dijkstra的算法思想,就是一开始将起点到起点的距离标记为0,而后进行n次循环,每次找出一个到起点距离dis[u]最短的点u,将它从蓝点变为白点。
随后枚举所有的蓝点vi,如果以此白点为中转到达蓝点vi的路径dis[u]+w[u][vi]更短的话,这将它作为vi的“更短路径”dis[vi](此时还不确定是不是vi的最短路径)。
就这样,我们每找到一个白点,就尝试着用它修改其他所有的蓝点。中转点先于终点变成白点,故每一个终点一定能够被它的最后一个中转点所修改,而求得最短路径。
Dijkstra步骤:
(1)初始时,S只包含源点,即S=v,距离为0。U包含除v外的其他顶点,U中顶点u距离为边上的权;
(2)从U中选取一个距离v最小的顶点k,把k加入S中(该选定的距离就是v到k的最短路径长度);
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值为经过顶点k的值(松弛操作,important!!);
(4)重复步骤(2)和(3)直到所有顶点都包含在S中。
下面我求下图,从顶点v1到其他各个顶点的最短路径
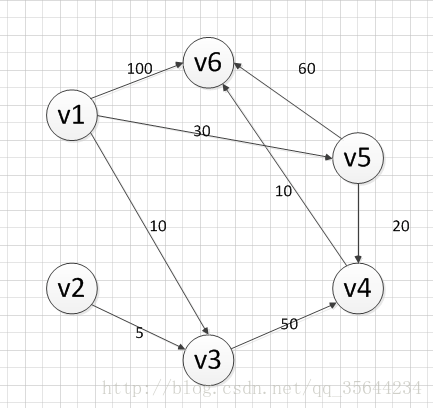
首先第一步,我们先声明一个dis数组,该数组初始化的值为:

我们的顶点集T的初始化为:T={v1}
既然是求 v1顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。
通过数组 dis 可知当前离v1顶点最近是 v3顶点。
当选择了 2 号顶点后,dis[2](下标从0开始)的值就已经从“估计值”变为了“确定值”,即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。
为什么呢?因为目前离 v1顶点最近的是 v3顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.
OK,既然确定了一个顶点的最短路径,下面我们就要根据这个新入的顶点V3会有出度,
发现以v3 为弧尾的有: < v3,v4 >,那么我们看看路径:v1–v3–v4的长度是否比v1–v4短,其实这个已经是很明显的了,因为dis[3]代表的就是v1–v4的长度为无穷大,而v1–v3–v4的长度为:10+50=60,所以更新dis[3]的值,得到如下结果:

因此 dis[3]要更新为 60。这个过程有个专业术语(好牛逼的样子)叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。
然后,我们又从除dis[2]和dis[0]外的其他值中寻找最小值,发现dis[4]的值最小,通过之前是解释的原理,可以知道v1到v5的最短距离就是dis[4]的值,然后,我们把v5加入到集合T中。
又然后,考虑v5的出度是否会影响我们的数组dis的值,v5有两条出度:< v5,v4>和 < v5,v6>,
再然后我们发现:v1–v5–v4的长度为:50,而dis[3]的值为60,所以我们要更新dis[3]的值.
v1-v5-v6的长度为:90,而dis[5]为100,所以我们需要更新dis[5]的值。更新后的dis数组如下图:

额然后,继续从dis中选择未确定的顶点的值中选择一个最小的值,发现dis[3]的值是最小的,所以把v4加入到集合T中,此时集合T={v1,v3,v5,v4}
嗯然后,考虑v4的出度是否会影响我们的数组dis的值,v4有一条出度:< v4,v6>,然后我们发现:v1–v5–v4–v6的长度为:60,而dis[5]的值为90,所以我们要更新dis[5]的值,更新后的dis数组如下图:

对然后,我们使用同样原理,分别确定了v6和v2的最短路径,最后dis的数组的值如下:

因此,从图中,我们可以发现v1-v2的值为:∞,代表没有路径从v1到达v2。所以我们得到的最后的结果为:
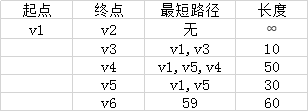
两种实现方法:
1.邻接矩阵+找最小边(简单缓慢)
2.邻接表+优先队列(复杂快速)
关键:
松弛操作
if(d[v]>d[u]+e[u][v].w) //如果源点经过u点距离v更短,更新d[v] d[v]=d[u]+e[u][v].w
稠密图的邻接矩阵:
for(int i=0;i<n;i++)//一共寻找n个点的最小dis { int x,m=inf; for(int y=0;y<n;y++) if(!vis[y]&&dis[y]<=m)//刷新最短dis m=dis[y],x=y; vis[x]=1; for(int y=0;y<n;y++) if(dis[y]>dis[x]+w[x][y])//刷新个点到原点距离 dis[y]=dis[x]+w[x][y]; }
邻接链表+优先队列:
memset(dis,127,sizeof(dis)); dis[1]=0; q.push(make_pair(dis[1],1)); while(!q.empty()) { int u=q.top().second;q.pop(); if(vis[u]) continue; vis[u]=1; for(int k=head[u];k!=-1;k=e[k].next) { if(dis[e[k].v]>dis[u]+e[k].w) { dis[e[k].v]=dis[u]+e[k].w; q.push(make_pair(dis[e[k].v],e[k].v)); }
路径输出:
方法一:从终点出发,不断顺着dis[y]==dis[x]+w[x][y]的边从y回到x,直到回到起点(太慢了),但更好的方法是方法二。
方法二:在更新时维护father指针 for(int y=0;y<n;y++) if(dis[y]>dis[x]+w[x][y]) father[y]=x;(即可一直递归)
邻接矩阵.练习:1261:【例9.5】城市交通路网
#pragma GCC optimize(2)//开O2,不用管,建议慎用(NOIP不准用) #include<cstdio> #include<string> #include<iostream> #include<cstring> #include<stdlib.h> using namespace std; const int maxn=101; const int inf=0x7f7f7f7f; int n; int map[maxn][maxn]; bool vis[maxn]; int dis[maxn]; int pre[maxn]; int f=1; int read() { int x=0,f=1;char c=getchar(); while(!isdigit(c)){ if(c=='-') f=-1; c=getchar(); } while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } return x*f; } void print(int x)//经典的输出函数 { if(x==0)return; else { print(pre[x]); printf("%d ",x+1); } } void work() { n=read(); memset(dis,inf,sizeof(dis)); for (int i=0;i<n;i++) for (int j=0;j<n;j++) { map[i][j]=read(); if(map[i][j]==0) map[i][j]=inf; else if(i==0) dis[j]=map[i][j]; } dis[0]=0; //printf("minlong=%d\n",dis[n-1]); //printf("%d",dis[4]); for(int i=0;i<n;i++) { int minn=inf,x=0; for (int j=0;j<n;j++) { if(!vis[j]&&minn>dis[j]) minn=dis[j],x=j; } vis[x]=1; //printf("%d\n",x); for (int j=0;j<n;j++) if(map[x][j]+dis[x]<dis[j]) { pre[j]=x; //我竟然卡了输出 dis[j]=map[x][j]+dis[x]; } } printf("minlong=%d\n",dis[n-1]); printf("1 "); print(n-1); } int main() { work(); return 0; }
邻接链表+优先队列.练习:RQNOJ 星门龙跃
#include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; typedef pair<int,int> pii; priority_queue<pii,vector<pii>,greater<pii> >q; struct edge{ int x,z,next; }e[300005]; int n,m,f[30005],vis[30005],tot=1,head[30005]; void adde(int u,int x,int z)//建树 { e[tot].x=x; e[tot].z=z; e[tot].next=head[u]; head[u]=tot++; } int main() { int a,b,c; memset(head,-1,sizeof(head)); memset(f,inf,sizeof(f)); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d%d",&a,&b,&c); adde(a,b,c); adde(b,a,c); } f[1]=0; q.push(make_pair(f[1],1)); while(!q.empty()) { int u=q.top().second; q.pop(); if(vis[u]) continue; vis[u]=1; for(int k=head[u];k!=-1;k=e[k].next) { int t=e[k].x; if(f[u]+e[k].z<f[t]) { f[t]=f[u]+e[k].z; q.push(make_pair(f[t],t)); } } } printf("%d",f[n]); return 0; }
——————————————————————————————————————————————————————
Floyd(暴力松弛):
算法的特点:
弗洛伊德算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。
算法的思路:
so easy,三层循环,第一层循环中间点k,第二第三层循环起点终点i、j,算法的思想很容易理解:如果点i到点k的距离加上点k到点j的距离小于原先点i到点j的距离,那么就用这个更短的路径长度来更新原先点i到点j的距离。(其实就是松弛)
动态规划原理
设d(i,j)为从i到j的只以(1…k)集合中的节点为中间点的最短路的长度;
1、若经过k,d(i,j)=d(i,k)+d(k,j)
2、若不经过k(可能经过1~k-1中的点),d(i,j)=d(i,j)
则d(i,j)=min(d(i,k)+d(k,j), d(i,j))(循环刷新最短路径)
我们求下图的每个点对之间的最短路径的过程如下:

第一步,我们先初始化两个矩阵,得到下图两个矩阵:
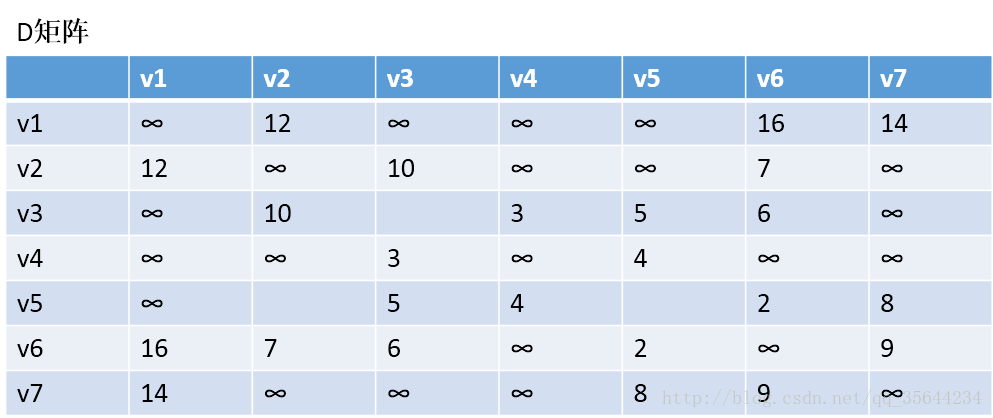
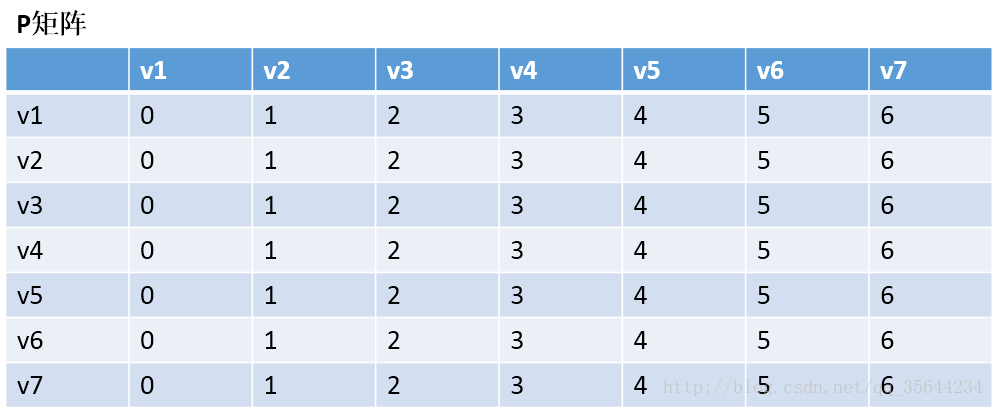
第二步,以v1为中阶,更新两个矩阵:
发现,a[1][0]+a[0][6] < a[1][6] 和a[6][0]+a[0][1] < a[6][1],所以我们只需要矩阵D和矩阵P,结果如下:
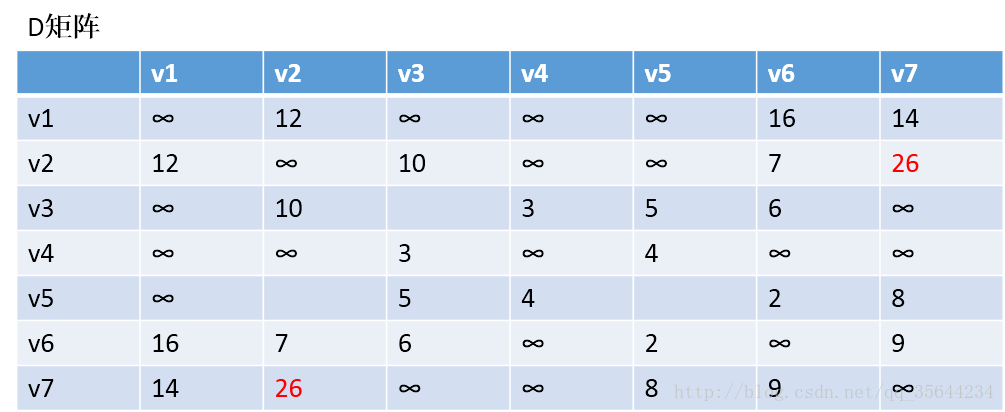
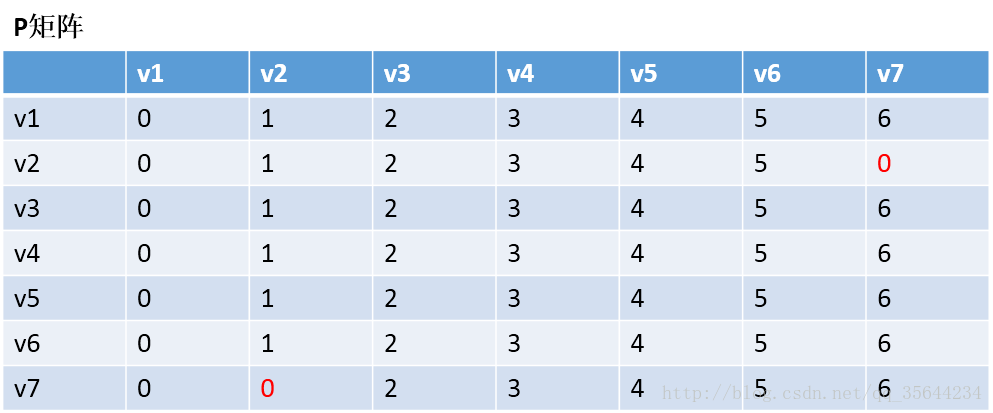
通过矩阵P,我发现v2–v7的最短路径是:v2–v1–v7
第三步:以v2作为中介,来更新我们的两个矩阵,使用同样的原理,扫描整个矩阵,得到如下图的结果:
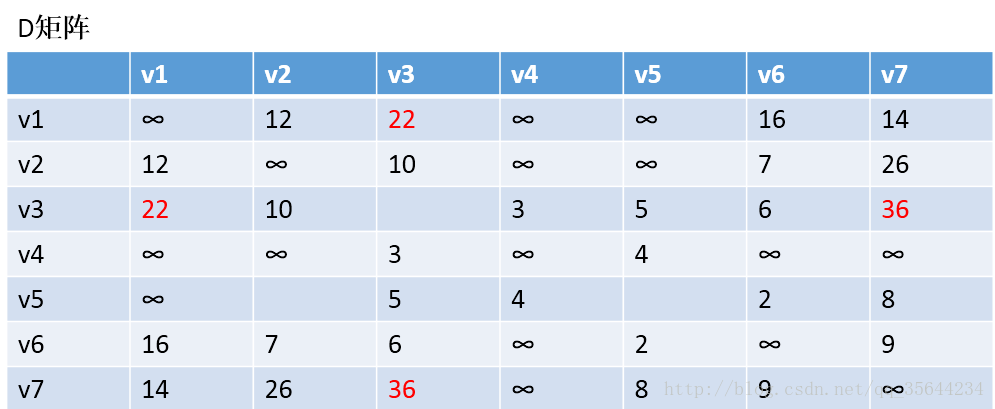
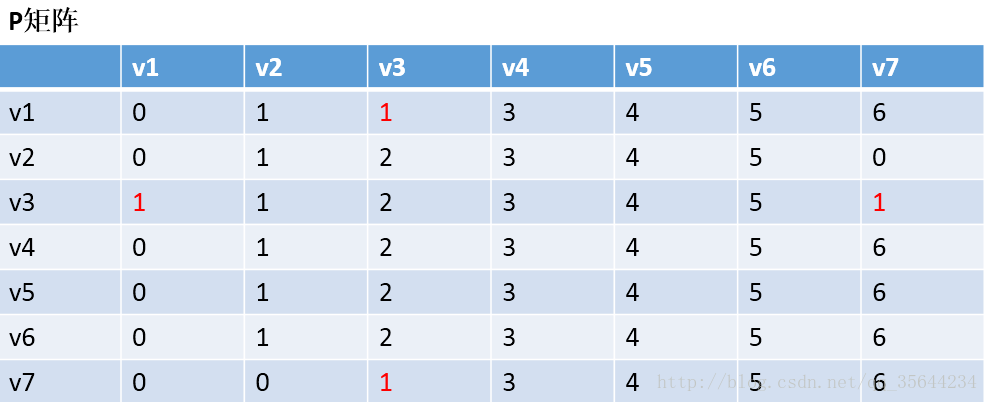
OK,到这里我们也就应该明白Floyd算法是如何工作的了,他每次都会选择一个中介点,然后,遍历整个矩阵,查找需要更新的值,下面还剩下五步,就不继续演示下去了,理解了方法,我们就可以写代码了。
详情:
for(k=0;k<n;k++)//k代表中间点必须放最外层 for(i=0;i<n;i++) for(j=0;j<n;j++) if(d[i][j]>d[i][k]+d[k][j]) d[i][j]= d[i][k]+d[k][j];
因为Floyd为O(N3),所以慎用,只在求任意两点(求多次)的情况下使用。
练习:自己练吧qaq.
—————————————————————————————————————————————————
Bellman-ford:
同样是用来计算从一个点到其他所有点的最短路径的算法,也是一种单源最短路径算法。 能够处理存在负边权的情况,但无法处理存在负权回路的情况。
算法步骤:
1、初始化:将除源点外的所有顶点最短距离估计值d[v]=inf,d[s]=0;
2、迭代求解:反复对边集E中每条边进行松弛操作,使得顶点集V中每个顶点v的最短距离估计值逐步逼近其最短距离;
3、检验负权回路:如果有存在点v,使得d[v]>d[u]+w[u][v],则有负权回路,返回false;
4、返回true,源点到v的最短距离保存在d[v]中。
算法分析&思想讲解:
Bellman-Ford算法的思想很简单。一开始认为起点是白点(dis[1]=0),每一次都枚举所有的边,必然会有一些边,连接着白点和蓝点。因此每次都能用所有的白点去修改所有的蓝点,每次循环也必然会有至少一个蓝点变成白点。
负权回路:
虽然Bellman-Ford算法可以求出存在负边权情况下的最短路径,却无法解决存在负权回路的情况。
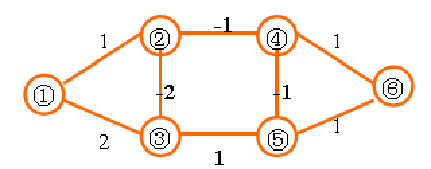
负权回路是指边权之和为负数的一条回路,上图中②-④-⑤-③-②这条回路的边权之和为-3。
在有负权回路的情况下,从1到6的最短路径是多少?答案是无穷小,因为我们可以绕这条负权回路走无数圈,每走一圈路径值就减去3,最终达到无穷小。
所以说存在负权回路的图无法求出最短路径,Bellman-Ford算法可以在有负权回路的情况下输出错误提示。
如果在Bellman-Ford算法的n-1重循环完成后,还是存在某条边使得:dis[u]+w<dis[v],
则存在负权回路: For每条边(u,v) If (dis[u]+w<dis[v]) return False
伪代码:
Bool bellman-ford(G,w,s) { for each vertex in V(G)d[v]=inf;d[s]=0; for(i=1;i<v;i++)//执行v-1次操作 for each egde(u,v) in E(G)//对每条边尝试松弛 if(d[v]>d[u]+w[u][v])d[v]=d[u]+w[u][v]; for each edge(u,v) in E(G)//v-1次松弛结束若还可以松弛,则有负环 if(d[v]>d[u]+w[u][v])return false; return true; }
——————————————————————————————————————————————————
SPFA:
我劝大家能用Bellman-ford,就用SPFA,毕竟SPFA是对Bellman的优化(也不复杂,Dijkstra的堆优化就复杂多了)
思想:
初始时将起点加入队列。每次从队列中取出一个元素,并对所有与它相邻的点进行修改,若某个相邻的点修改成功,则将其入队。直到队列为空时算法结束。利用了每个点不会更新次数太多的特点发明的此算法。
SPFA 在形式上和广度优先搜索非常类似。
不同的是广度优先搜索中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是说一个点修改过其它的点之后,过了一段时间可能会获得更短的路径,于是再次用来修改其它的点,这样反复进行下去。
算法时间复杂度:O(kE),E是边数。K是常数,平均值为2。
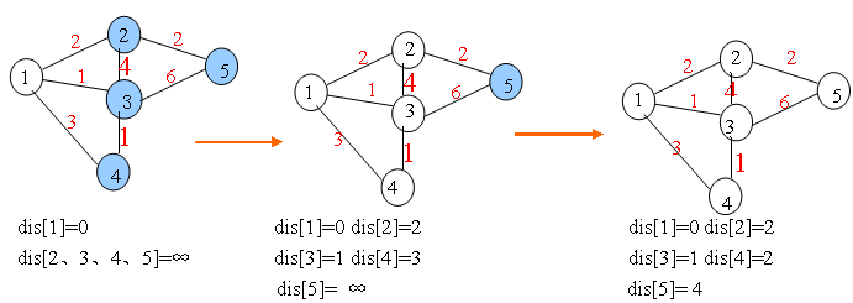
下面我们采用SPFA算法对下图求v1到各个顶点的最短路径,通过手动的方式来模拟SPFA每个步骤的过程

初始化:
首先我们先初始化数组dis如下图所示:(除了起点赋值为0外,其他顶点的对应的dis的值都赋予无穷大,这样有利于后续的松弛)

此时,我们还要把v1如队列:{v1}
现在进入循环,直到队列为空才退出循环。第一次循环:
首先,队首元素出队列,即是v1出队列,然后,对以v1为弧尾的边对应的弧头顶点进行松弛操作,可以发现v1到v3,v5,v6三个顶点的最短路径变短了,更新dis数组的值,得到如下结果:

我们发现v3,v5,v6都被松弛了,而且不在队列中,所以要他们都加入到队列中:{v3,v5,v6}
第二次循环
此时,队首元素为v3,v3出队列,然后,对以v3为弧尾的边对应的弧头顶点进行松弛操作,可以发现v1到v4的边,经过v3松弛变短了,所以更新dis数组,得到如下结果:

第三次循环
此时,队首元素为v5,v5出队列,然后,对以v5为弧尾的边对应的弧头顶点进行松弛操作,发现v1到v4和v6的最短路径,经过v5的松弛都变短了,更新dis的数组,得到如下结果:
我们发现v4、v6对应的值都被更新了,但是他们都在队列中了,所以不用对队列做任何操作。队列值为:{v6,v4}、

第四次循环
此时,队首元素为v6,v6出队列,然后,对以v6为弧尾的边对应的弧头顶点进行松弛操作,发现v6出度为0,所以我们不用对dis数组做任何操作,其结果和上图一样,队列同样不用做任何操作,它的值为:{v4}
第五次循环
此时,队首元素为v4,v4出队列,然后,对以v4为弧尾的边对应的弧头顶点进行松弛操作,可以发现v1到v6的最短路径,经过v4松弛变短了,所以更新dis数组,得到如下结果:

因为我修改了v6对应的值,而且v6也不在队列中,所以我们把v6加入队列,{v6}
第六次循环
此时,队首元素为v6,v6出队列,然后,对以v6为弧尾的边对应的弧头顶点进行松弛操作,发现v6出度为0,所以我们不用对dis数组做任何操作,其结果和上图一样,队列同样不用做任何操作。所以此时队列为空。
OK,队列循环结果,此时我们也得到了v1到各个顶点的最短路径的值了,它就是dis数组各个顶点对应的值,如下图:

伪代码:
q.push(s);vis[s]=1; void spfa() { while(!q.empty()) u=q.front();q.pop();vis[u]=0;//出队标记 for each v in adj(u) { if(dis[v]>d[u]+w[u][v]) { dis[v]=d[u]+w[u][v]; if(!vis[v]){q.push(v);vis[v]=1;} } } }
例题:RQONJ星门龙跃
#include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f #define maxm 30001 using namespace std; queue<int> q; struct edge{ int x,z,next; }e[150001]; int n,m,f[maxm],vis[maxm],tot=1,head[maxm]; void adde(int u,int x,int z) { e[tot].x=x; e[tot].z=z; e[tot].next=head[u]; head[u]=tot++; e[tot].x=u; e[tot].z=z; e[tot].next=head[x]; head[x]=tot++; } int main() { int a,b,c,p; memset(head,-1,sizeof(head)); memset(f,inf,sizeof(f)); memset(vis,0,sizeof(vis)); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d%d",&a,&b,&c); adde(a,b,c); } f[1]=0; q.push(1); vis[1]=1; while(!q.empty()) { int u=q.front(); q.pop(); vis[u]=0; for(int k=head[u];k!=-1;k=e[k].next) { p=e[k].x; if(f[p]>f[u]+e[k].z) { f[p]=f[u]+e[k].z; if(!vis[p]) { q.push(p); vis[p]=1; } } } } printf("%d",f[n]); return 0; }
三种最短路算法
1、dijkstra(单源点最短路):贪心的思想,每次从集合U中找一个离源点最近的点加入到集合S中,并以新加入的点作为中间点松弛U中的点到源点的距离。直到U为空算法结束。也就是一个一个的求出最短路径
使用优先队列优化。队列中存储的是U中点的子集。
不能处理负权存在的情况。
复杂度远小于O(M*N),因为贪心所以速度三者中最快,用二项堆优化到 O(ElogV) 。
2、Bellman-Ford (单源点最短路):对所有边,进行k遍松弛操作,就会计算出与源点最多由k条边相连的点的最短路。 也就是不断刷新最短路
因为最短路一定不含环,所以最多包含n-1条边,那么我们进行n-1遍松弛操作就可以计算出所有点的最短路。
每次计算时,那些已经算出来最短路的点不用重复计算,可使用队列优化(SPFA)。
可含负边权。
复杂度为远小于O(M*N)
3、Floyd(多源点最短路):点i到j的最短路有两种情况,
1:i直接到j。
2:i经过k到j。
所以对于每个中间点k,枚举它的起点和终点,进行松弛操作,最终将得到所有点的最短路。
邻接矩阵存储,可含负边权。
复杂度O(N^3)。
谢谢大家,有错请再评论区指出




