浅说——最小生成树
设有图G(V,E).
w(u,v)表示边(u,v)的权。
生成树是G的极小连通子图,它包含原图的n个点和n-1条边,且是连通的。
若存在树T,使得边权之和W(T)最小,则T为最小生成树。
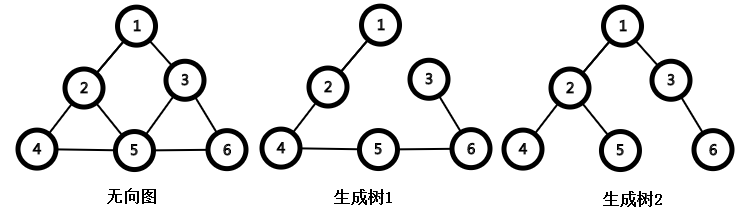
例:(来了来了…)
要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信。
但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同。
次要目标是要使铺设光缆的总费用最低。
这里讲两种方法:
Kruskal算法(克鲁斯卡尔):贪心策略,不断加边
Prim算法(普里姆):贪心策略,不断加点
Kruskal算法:
先构造一个只含 n 个顶点,而边集为空的子图。(开始加边)
之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,也就是说,将这两个顶点分别所在的两棵树合成一棵树;反之,若该条边的两个顶点已落在同一棵树上,则不可取(已经到过了)
而应该取下一条权值最小的边再试之。依次类推,直至森林中只有一棵树,也即子图中含有 n-1条边为止。
从最短边开始加,若未经历节点,则加入树。

伪代码
sort(e+1,e+m+1); 初始化MST=NULL; 初始化各点各自为一个集合; for(int i=0;i<m;i++)
{ if(e[i].u和e[i].v不在一个集合) { 将e[i]加入MST; 合并e[i].u和e[i].v所在的集合; }
}
该算法中关键在于解决判断u,v是否在同一集合和将其合并的操作,这里我们使用一种简单高效的方法:并查集。
并查集是一种树型的数据结构,用于处理一些点所在集合的合并及查询问题。常常在使用中以森林来表示。
算法步骤
初始化:把每个点所在集合初始化为其自身。
查找:查找元素所在的集合,即根节点。
合并:将两个元素所在的集合合并为一个集合。合并之前,应先判断两个元素是否属于同一集合,这可用上面的“查找”操作实现。
void chushi() {//初始化 for(int i=0;i<n;i++)father[i]=i; } int find(int x) {//查找 if(father[x]==x)return x; return father[x]=find(father[x]); }//路径压缩 void unionset(int x,int y)//合并 { int fx=find(x);//查找x的所在树的根 int fy=find(y);//查找y的所在树的根 if(fx!=fy)father[fx]=fy;//将x所在集合与y所在集合合并 }
自己拿演草纸推论一下就出来了
模板题:
#include<cstdio> #include<algorithm> using namespace std; const int maxn=1005; int n,m,ans; int fa[maxn]; struct edge{ int x,y,v; }e[maxn*maxn]; int find(int x) //查找父亲节点 { if(fa[x]==x) return x; return fa[x]=find(fa[x]); } bool cmp(struct edge a,struct edge b) { return a.v<b.v; } void kruskall() { int cnt=0; sort(e+1,e+m+1,cmp); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) { if(cnt==n-1) break; int fx=find(e[i].x); int fy=find(e[i].y); if(fx!=fy) { fa[fx]=fy; //合并两棵树 cnt++; ans+=e[i].v; } } printf("%d",ans); } int main() { int x,y,a; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d%d",&x,&y,&a); e[i].x=x; e[i].y=y; e[i].v=a; } kruskall(); return 0; }
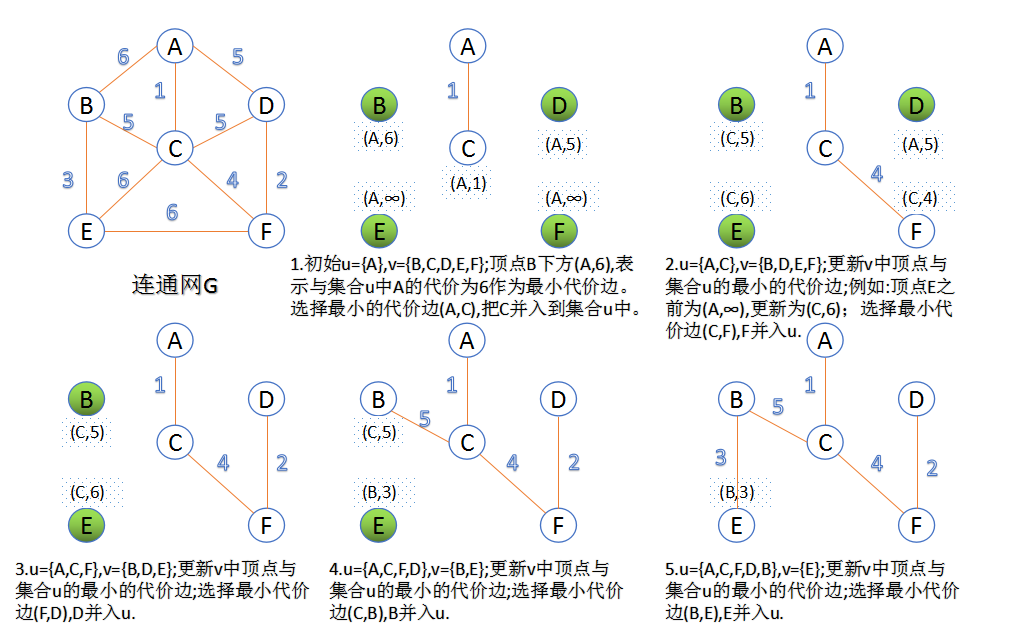
Prim算法
1、设立一个只有结点u0的结点集U和一个空的边集E作为最小生成树的初始形态;
2、在所有u∈U,v∈(V-U)的边(u,v)∈E中,找一条权最小的边(u0,v0),将此边加进集合E中,并将此边的非U中顶点加入U中。
3、如果U=V,则算法结束;否则重复步骤2。
还是看图吧
伪代码
for(int i=1;i<=n;i++)dis[i]=inf; dis[1]=0; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) 找dis[j]最小&&vis[j]==0的点j, vis[j]=1; 更新j->k的dis[k]; }
#include<cstdio> #include<cstring> #include<algorithm> #define inf 0x3f3f3f3f using namespace std; const int maxn=1005; int n,m,ans,cnt=1; int fa[maxn],head[maxn],dis[maxn],vis[maxn]; struct edge{ int x,y,v,next; }e[maxn*maxn]; void addedge(int x,int y,int a)//邻接矩阵 { e[cnt].x=x; e[cnt].y=y; e[cnt].v=a; e[cnt].next=head[x]; head[x]=cnt++; } void primm() { int mi; memset(dis,inf,sizeof(dis)); dis[1]=0; int u; for(int i=1;i<=n;i++) { mi=inf; for(int j=1;j<=n;j++) if(!vis[j]&&mi>dis[j]) { mi=dis[j];u=j; } vis[u]=1; ans+=mi; for(int k=head[u];k!=-1;k=e[k].next) { if(dis[e[k].y]>e[k].v) dis[e[k].y]=e[k].v; } } printf("%d",ans); } int main() { int x,y,a; scanf("%d%d",&n,&m); memset(head,-1,sizeof(head)); for(int i=1;i<=m;i++) { scanf("%d%d%d",&x,&y,&a); addedge(x,y,a); addedge(y,x,a); } primm(); return 0; }
时间复杂度:
Kruskal:O(MlogM)
Prim:O(N^2),可以用二项堆优化到O(MlogV)。
对于稠密图Prim更好,稀疏图Kruskal更佳(且算法更简)



