动态规划
目录
背包dp

0/1背包
模板题 acwing.2. 01背包问题
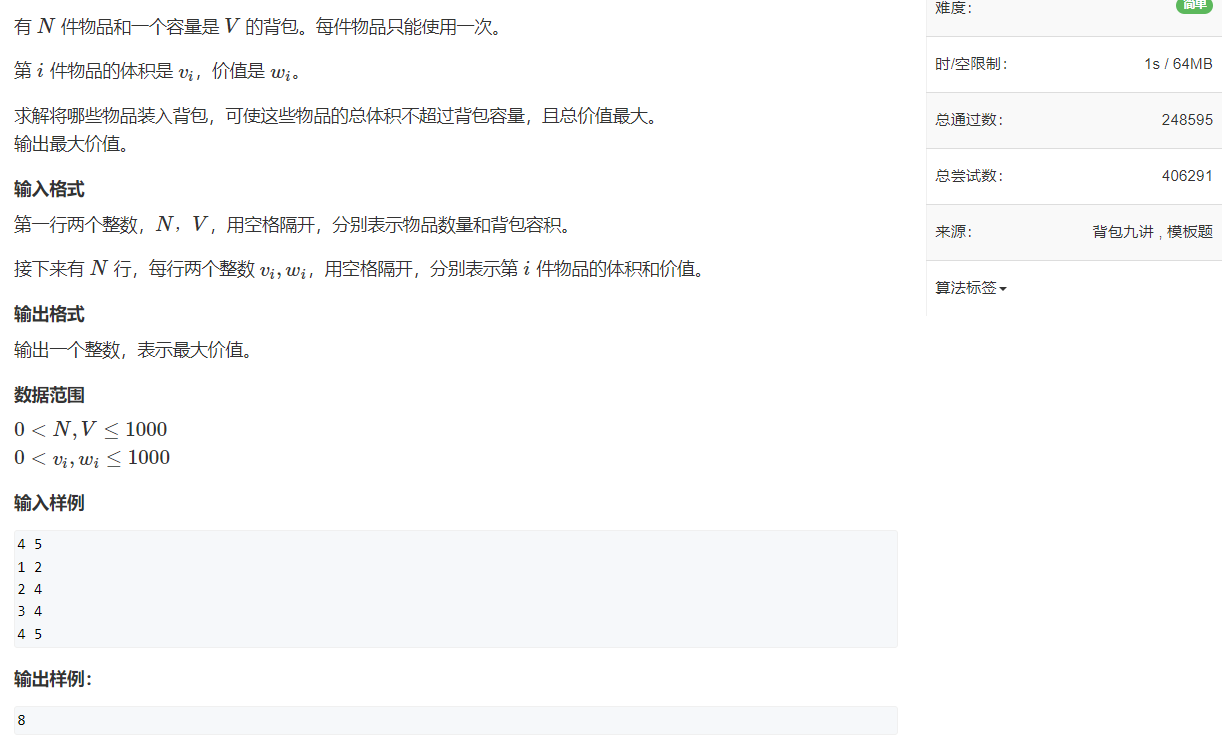
0/1背包 & 朴素版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//不选第i个物品时,f[i][j] = f[i-1][j]
//选第i个物品时,f[i][j] = f[i-1][j-v[i]]+w[i],保证j>=v[i]
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
}
printf("%d", f[n][m]);
return 0;
}
0/1背包 & 滚动数组
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[2][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i&1][j] = f[(i-1)&1][j];
if(j>=v[i]) f[i&1][j] = max(f[i&1][j], f[(i-1)&1][j-v[i]] + w[i]);
}
}
printf("%d", f[n&1][m]);
return 0;
}
0/1背包 & 终极版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
完全背包
模板题 acwing. 3. 完全背包问题
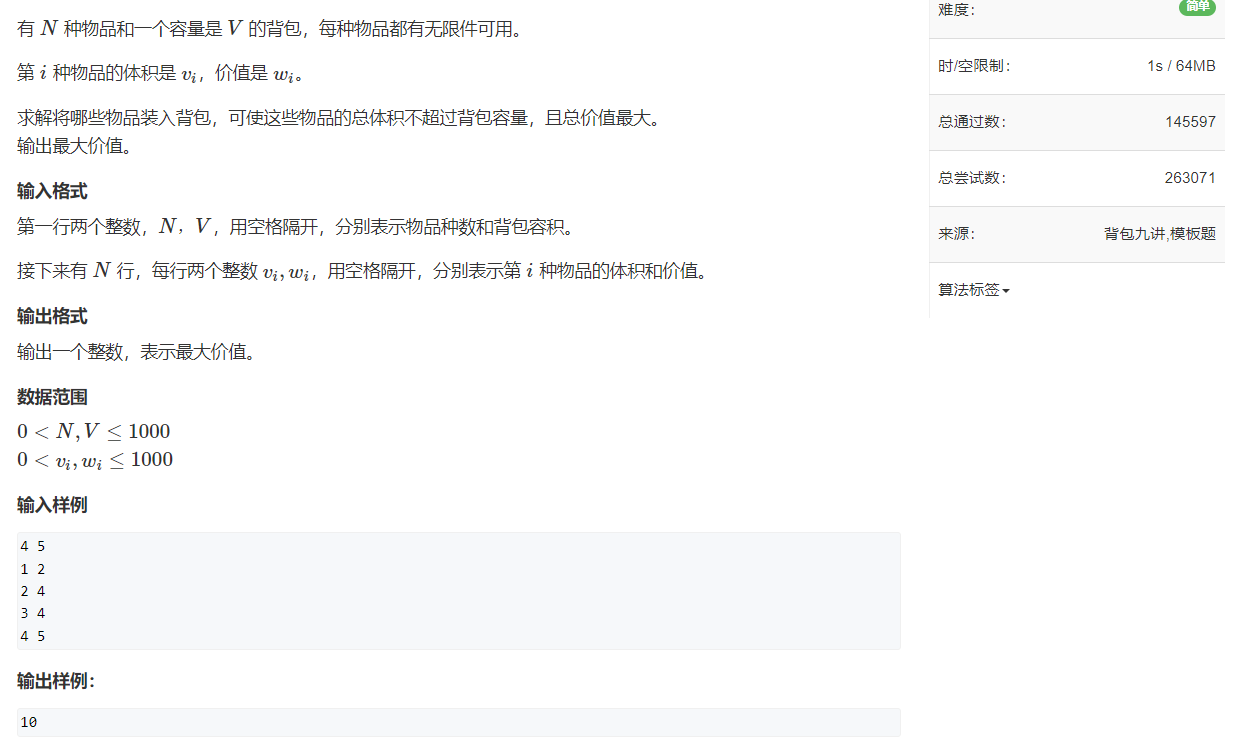
完全背包 & 朴素版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//f[i][j]=max(f[i-1][j], f[i-1][j], f[i-1][j-v[i]]+w[i], f[i-1][j-2*v[i]]+2*w[i], ....)
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
for(int k=0; k*v[i]<=j; k++)
{
f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
}
}
}
printf("%d", f[n][m]);
return 0;
}
完全背包 & 二维数组版

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
//f[i][j]表示前i个物品,体积不超过j时的最大价值
//f[i][j] = max(f[i-1][j], f[i][j-v] + w)
int f[maxn][maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]);
}
}
printf("%d", f[n][m]);
return 0;
}
完全背包 & 终极版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int f[maxn] = {}; //默认全为0,这样后面就不需要再初始化
int n = 0, m = 0; //n件物品,m为背包总容量
int v[maxn] = {}, w[maxn] = {}; //v表示第i件物品体积,w为第i件物品价值
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i=1; i<=n; i++)
{
for(int j=v[i]; j<=m; j++)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
多重背包
模板题 acwing. 4. 多重背包问题 I
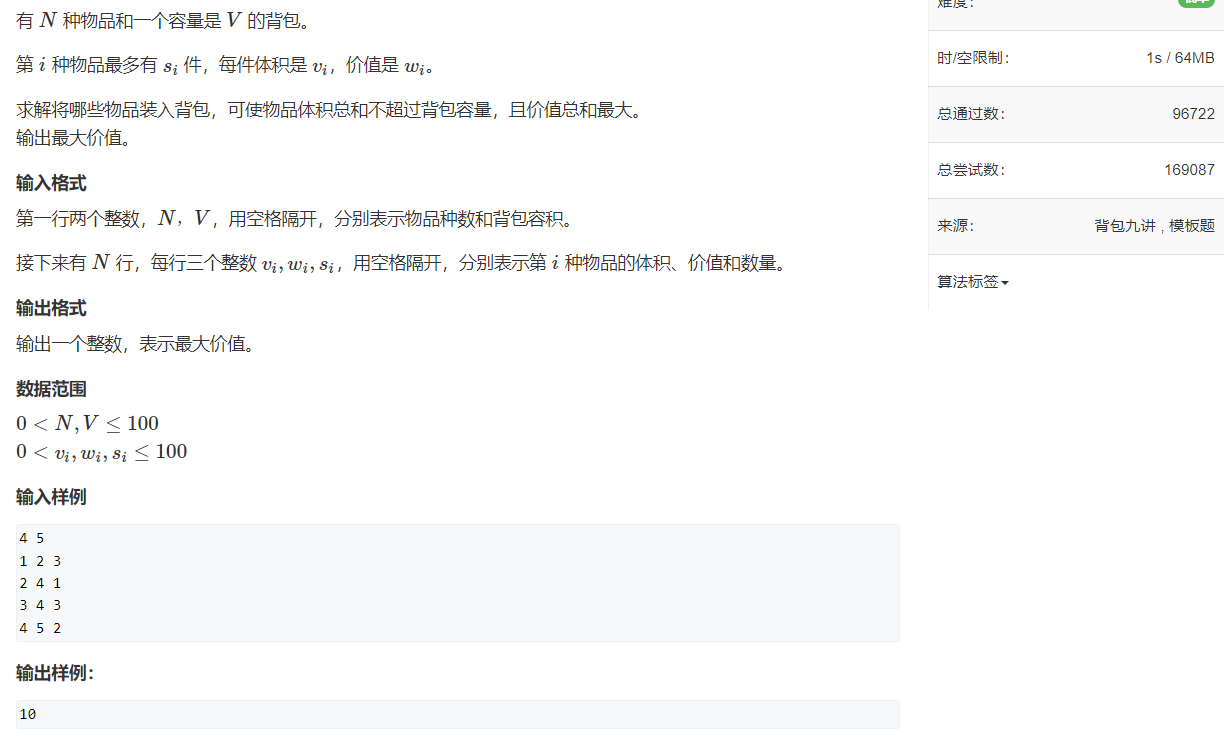
直接转化为0/1背包
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
int n = 0, m = 0;
int f[maxn] = {};
int v[maxn] = {}, w[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &w[i], &s[i]);
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=s[i]; j++)
{
for(int k=m; k>=v[i]; k--)
{
f[k] = max(f[k], f[k-v[i]] + w[i]);
}
}
}
printf("%d", f[m]);
return 0;
}
多重背包 & 二进制拆分
#include <bits/stdc++.h>
using namespace std;
const int maxn = 15000;
const int maxm = 2010;
int n = 0, m = 0;
int f[maxm] = {};
int v[maxn] = {}, w[maxn] = {}, s[maxn] = {}, cnt = 0;
int main()
{
int vi = 0, wi = 0, si = 0;
scanf("%d%d", &n, &m);
//二进制拆分
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &vi, &wi, &si);
if(si > m / vi) si = m / vi;
for(int j=1; j<=si; j<<=1)
{
v[++cnt] = j * vi;
w[cnt] = j * wi;
si -= j;
}
if(si > 0)
{
v[++cnt] = si * vi;
w[cnt] = si * wi;
}
}
//0/1背包
for(int i=1; i<=cnt; i++)
{
for(int j=m; j>=v[i]; j--)
{
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d", f[m]);
return 0;
}
分组背包
模板题 提高题库 246.分组背包
分组背包 & 朴素版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 40;
const int maxm = 210;
//分组背包
int n = 0, m = 0, t = 0;
int v[maxn] = {}, c[maxn] = {};
//g[i][j]表示第i组第j个物品的编号
int g[15][maxn] = {};
//f[i][j]表示前i组物品,体积不超过j的最大价值
int f[15][maxm] = {};
int main()
{
int x = 0;
scanf("%d%d%d", &m, &n, &t);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &c[i], &x);
g[x][++g[x][0]] = i;
}
for(int i=1; i<=t; i++)
{
for(int j=0; j<=m; j++)
{
f[i][j] = f[i-1][j];
for(int k=1; k<=g[i][0]; k++)
{
if(j >= v[g[i][k]])
{
x = g[i][k];
f[i][j] = max(f[i][j], f[i-1][j-v[x]] + c[x]);
}
}
}
}
printf("%d", f[t][m]);
return 0;
}
分组背包 & 终极版1
#include <bits/stdc++.h>
using namespace std;
const int maxn = 40;
const int maxm = 210;
//分组背包
int n = 0, m = 0, t = 0;
int v[maxn] = {}, c[maxn] = {}, g[15][maxn] = {};
int f[maxm] = {};
int main()
{
int x = 0;
scanf("%d%d%d", &m, &n, &t);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &v[i], &c[i], &x);
g[x][++g[x][0]] = i;
}
for(int i=1; i<=t; i++)
{
for(int j=m; j>=0; j--)
{
for(int k=1; k<=g[i][0]; k++)
{
if(j >= v[g[i][k]])
{
x = g[i][k];
f[j] = max(f[j], f[j-v[x]] + c[x]);
}
}
}
}
printf("%d", f[m]);
return 0;
}
分组背包 & 终极版2
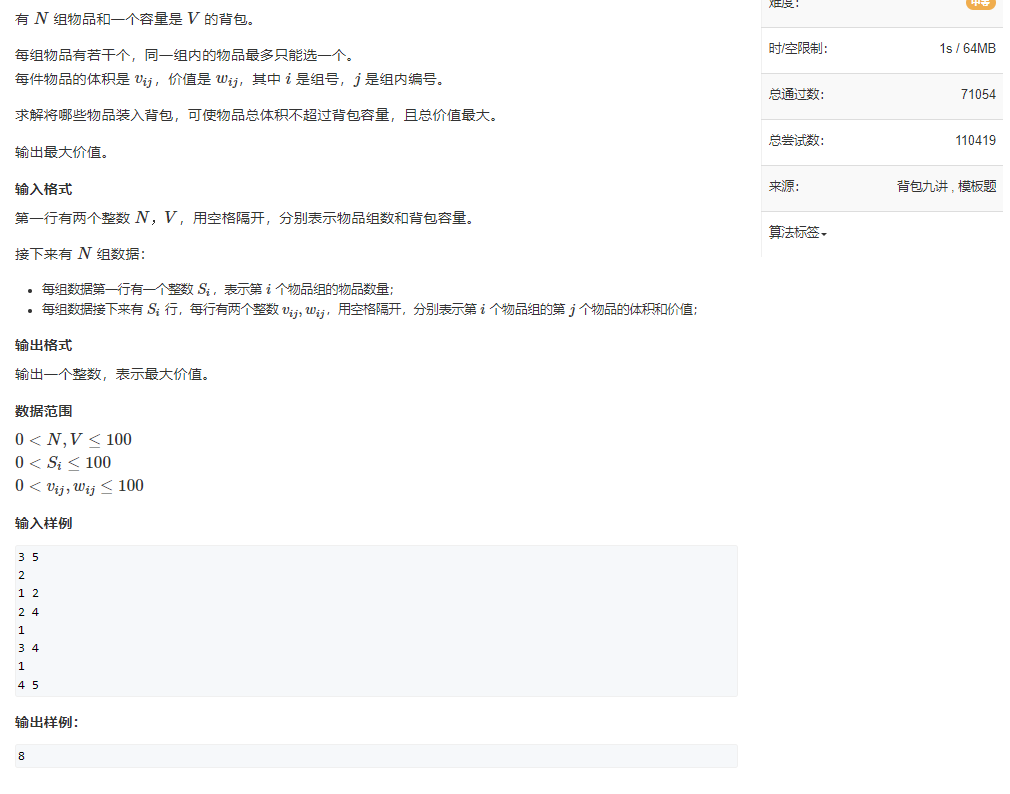
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
const int maxm = 110;
int n = 0, m = 0;
int f[maxm] = {};
int v[maxn][maxn] = {}, w[maxn][maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
scanf("%d", &s[i]);
for(int j=1; j<=s[i]; j++)
{
scanf("%d%d", &v[i][j], &w[i][j]);
}
}
for(int i=1; i<=n; i++) //阶段
{
//i和j共同构成状态
for(int j=m; j>=0; j--)
{
for(int k=1; k<=s[i]; k++) //k是决策
{
if(j >= v[i][k])
{
f[j] = max(f[j], f[j-v[i][k]] + w[i][k]);
}
}
}
}
printf("%d", f[m]);
return 0;
}
二维费用背包
二维费用背包 & 朴素版
模板题:提高组题库 245.NASA的食物计划
#include <bits/stdc++.h>
using namespace std;
const int maxn = 60;
const int maxm = 410;
//二维费用背包
int n = 0, v = 0, m = 0;
int a[maxn] = {}, b[maxn] = {}, c[maxn] = {};
int f[maxn][maxm][maxm] = {};
int main()
{
scanf("%d%d%d", &v, &m, &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &a[i], &b[i], &c[i]);
}
for(int i=1; i<=n; i++)
{
for(int j=0; j<=v; j++)
{
for(int k=0; k<=m; k++)
{
f[i][j][k] = f[i-1][j][k];
if(j>=a[i] && k>=b[i]) f[i][j][k] = max(f[i][j][k], f[i-1][j-a[i]][k-b[i]] + c[i]);
}
}
}
printf("%d", f[n][v][m]);
return 0;
}
二维费用背包 & 终极版
#include <bits/stdc++.h>
using namespace std;
const int maxn = 60;
const int maxm = 410;
//二维费用背包
int n = 0, v = 0, m = 0;
int a[maxn] = {}, b[maxn] = {}, c[maxn] = {};
int f[maxm][maxm] = {};
int main()
{
scanf("%d%d%d", &v, &m, &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &a[i], &b[i], &c[i]);
}
for(int i=1; i<=n; i++)
{
for(int j=v; j>=a[i]; j--)
{
for(int k=m; k>=b[i]; k--)
{
f[j][k] = max(f[j][k], f[j-a[i]][k-b[i]] + c[i]);
}
}
}
printf("%d", f[v][m]);
return 0;
}
线性dp
三道经典例题
数字三角形
acwing 898. 数字三角形
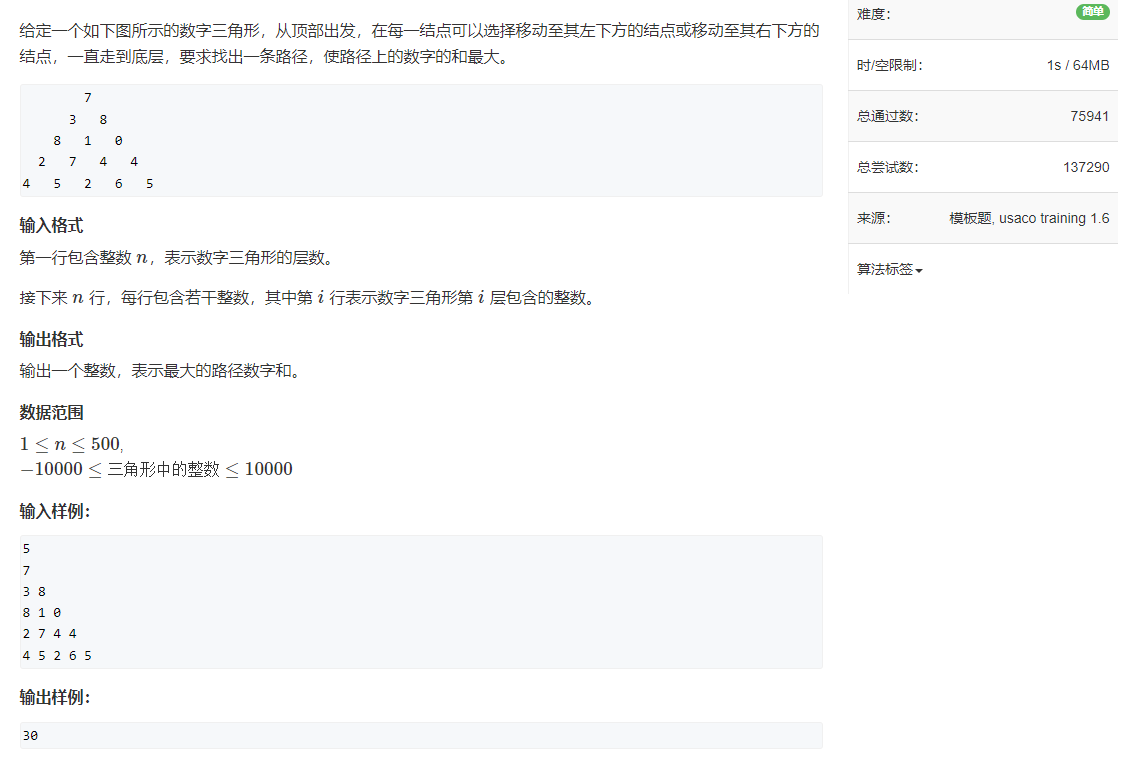
#include <bits/stdc++.h>
using namespace std;
const int maxn = 510;
const int inf = 0x3f3f3f3f;
int n = 0, m = 0;
int a[maxn][maxn] = {};
//f[i][j]表示到达第i行j列这个位置的最大值
int f[maxn][maxn] = {};
int main()
{
scanf("%d", &n);
//读入三角形数据
for(int i=1; i<=n; i++)
{
for(int j=1; j<=i; j++)
{
scanf("%d", &a[i][j]);
}
}
//初始化f
for(int i=0; i<=n; i++)
{
for(int j=0; j<=n; j++)
{
f[i][j] = -inf;
}
}
//线性dp
f[0][0] = 0;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=i; j++)
{
f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j];
}
}
int ans = -inf;
for(int i=1; i<=n; i++)
{
ans = max(ans, f[n][i]);
}
printf("%d", ans);
return 0;
}
最长上升序列(LIS)
提高组题库 216.求最长上升序列
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
const int inf = 0x3f3f3f3f;
int n = 0;
int a[maxn] = {};
//f[i]表示到第i个数中的最长上升降序列长度
//a[i]>a[j]时 f[i] = max(f[i], f[j] + 1) 1<=j<i
int f[maxn] = {}, ans = 1, pre[maxn];
void p(int x)
{
if(x == 0) return;
p(pre[x]);
printf("%d ", a[x]);
}
int main()
{
int x = 0, te = 0;
while(scanf("%d", &x) != EOF) a[++n] = x;
for(int i=1; i<=n; i++)
{
f[i] = 1;
for(int j=1; j<i; j++)
{
if(a[i]>a[j] && f[i]<f[j]+1)
{
f[i] = f[j] + 1;
pre[i] = j;
if(ans < f[i])
{
ans = f[i];
te = i;
}
}
}
}
printf("max=%d\n", ans);
p(te);
return 0;
}
区间dp
例题
石子合并1
提高组题库,265.石子合并<1>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
int n = 0;
//f[i][j]表示i~j堆这个区间的总分最少
//f[i][j]=min(f[i][j], f[i][k]+f[k+1][j]+s[j]-s[i-1]),k属于i~j-1
//g[i][j]表示i~j堆这个区间的总分最多
int f[maxn][maxn] = {}, g[maxn][maxn] = {};
//s表示a的前缀和
int a[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
s[i] = s[i-1] + a[i];
}
//f表示最小值,所以都初始化为极大值
memset(f, 0x3f, sizeof(f));
//只有一个石子的时候,不能合并,因此初始化为0
for(int i=1; i<=n; i++) f[i][i] = 0;
for(int len=2; len<=n; len++) //阶段,区间长度
{
for(int i=1; i<=n-len+1; i++)
{
int j = i + len - 1;
for(int k=i; k<j; k++)
{
f[i][j] = min(f[i][j], f[i][k]+f[k+1][j]+s[j]-s[i-1]);
g[i][j] = max(g[i][j], g[i][k]+g[k+1][j]+s[j]-s[i-1]);
}
}
}
printf("%d\n%d\n", f[1][n], g[1][n]);
return 0;
}
石子合并2
提高组题库,266.石子合并<2>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 210;
int n = 0;
//f[i][j]表示i~j堆这个区间的总分最少
//f[i][j]=min(f[i][j], f[i][k]+f[k+1][j]+s[j]-s[i-1]),k属于i~j-1
//g[i][j]表示i~j堆这个区间的总分最多
int f[maxn][maxn] = {}, g[maxn][maxn] = {};
//s表示a的前缀和
int a[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
a[n+i] = a[i];
}
for(int i=1; i<=n*2; i++) s[i] = s[i-1] + a[i];
//f表示最小值,所以都初始化为极大值
memset(f, 0x3f, sizeof(f));
//只有一个石子的时候,不能合并,因此初始化为0
for(int i=1; i<=n*2; i++) f[i][i] = 0;
for(int len=2; len<=n; len++) //阶段,区间长度
{
for(int i=1; i<=2*n-len+1; i++)
{
int j = i + len - 1;
for(int k=i; k<j; k++)
{
f[i][j] = min(f[i][j], f[i][k]+f[k+1][j]+s[j]-s[i-1]);
g[i][j] = max(g[i][j], g[i][k]+g[k+1][j]+s[j]-s[i-1]);
}
}
}
int ans1 = 0x7fffffff, ans2 = 0;
for(int i=1; i<=n; i++)
{
ans1 = min(ans1, f[i][n+i-1]);
ans2 = max(ans2, g[i][n+i-1]);
}
printf("%d\n%d\n", ans1, ans2);
return 0;
}
石子合并3
提高组题库,267.石子合并<3>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 4010;
int n = 0;
//f[i][j]表示i~j堆这个区间的总分最多
//1、f[i][j]由f[i+1][j]与a[i]合并而来
//2、f[i][j]由f[i][j-1]与a[j]合并而来
int f[maxn][maxn] = {};
//s表示a的前缀和
int a[maxn] = {}, s[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
a[n+i] = a[i];
}
for(int i=1; i<=n*2; i++) s[i] = s[i-1] + a[i];
for(int len=2; len<=n; len++) //阶段,区间长度
{
for(int i=1; i<=2*n-len+1; i++)
{
int j = i + len - 1;
f[i][j] = max(f[i+1][j], f[i][j-1]) + s[j] - s[i-1];
}
}
int ans = 0;
for(int i=1; i<=n; i++)
{
ans = max(ans, f[i][n+i-1]);
}
printf("%d\n", ans);
return 0;
}
状态压缩dp
例题
特殊方格棋盘
提高组题库 313.特殊方格棋盘
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n = 0, m = 0;
int a[25] = {};
//f[i]表示前j(j为i的二进制表示中1的个数)行中最大的方案数
//比如i的二进制为010110,则表示前三行最大的方案数
//最后结果为f[(i<<n)-1]
ll f[(1<<20) + 5] = {};
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
a[x] |= (1<<(y-1)); //记录x行y-1列不能放置,因为下标从0开始,所以是y-1
}
f[0] = 1;
for(int i=1; i<(1<<n); i++)
{
//当状态为i时,找到i的二进制中有k个1,即表示当前为第k行
int k = 0;
for(int j=0; j<n; j++)
{
if(i & (1<<j)) k++;
}
for(int j=0; j<n; j++)
{
if(a[k] & (1<<j)) continue;
//^相同为0,不同为1.其实就是枚举如:0111是由0101,0110,0011情况和
if(i & (1<<j)) f[i] += f[i ^ (1<<j)];
}
}
printf("%lld\n", f[(1<<n)-1]);
return 0;
}



