数据结构模板
目录
数据结构
离散化
结构体实现
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//5
//9 1 0 5 4
int n = 0;
struct node
{
int x, id;
}a[maxn];
int b[maxn] = {};
bool cmp(node &nd1, node &nd2)
{
return nd1.x < nd2.x;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i].x);
a[i].id = i;
}
sort(a+1, a+1+n, cmp);
for(int i=1; i<=n; i++) b[a[i].id] = i;
for(int i=1; i<=n; i++) printf("%d ", b[i]);
}
使用STL实现-方法一
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//6
//9 1 1 0 5 4
int n = 0;
int a[maxn] = {}, b[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(a+1, a+1+n);
int cnt = unique(a+1, a+1+n) - (a+1);
for(int i=1; i<=n; i++)
{
b[i] = lower_bound(a+1, a+1+cnt, b[i]) - a;
}
for(int i=1; i<=n; i++) printf("%d ", b[i]);
}
使用STL实现-方法二
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100;
//input:
//5
//9 1 0 5 4
int n = 0;
map<int, int> mp;
int cnt = 0;
int a[maxn] = {}, b[maxn] = {};
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
sort(a+1, a+1+n);
for(int i=1; i<=n; i++) mp[a[i]] = ++cnt;
for(int i=1; i<=n; i++) printf("%d ", mp[b[i]]);
}
并查集
朴素并查集
例题:提高题库 161.亲戚
#include <bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 20010;
int n = 0, m = 0, q = 0;
int fa[maxn] = {};
//查找祖先节点
int getfa(int x)
{
if(x == fa[x]) return fa[x];
return fa[x] = getfa(fa[x]);
}
//将y合并到x
void merge(int x, int y)
{
int fx = getfa(x);
int fy = getfa(y);
if(fx != fy) fa[fy] = fx;
}
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
//初始化
for(int i=1; i<=n; i++) fa[i] = i;
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
merge(x, y);
}
scanf("%d", &q);
for(int i=1; i<=q; i++)
{
scanf("%d%d", &x, &y);
int fx = getfa(x);
int fy = getfa(y);
if(fx == fy) printf("Yes\n");
else printf("No\n");
}
return 0;
}
维护size的并查集
例题:提高题库 163.打击犯罪
const int maxn = 1010;
int n = 0;
//fa[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
int fa[maxn] = {}, size[maxn] = {};
//返回x的祖宗节点
int findset(int x)
{
if(fa[x] != x) fa[x] = findset(fa[x]);
return fa[x];
}
//合并a和b所在的两个集合:
void merge(int x, int y)
{
int fx = findset(x), fy = findset(y);
if(fx != fy)
{
fa[fy] = fx;
size[fx] += size[fy];
}
}
//初始化,假定节点编号是1~n
for(int i=1; i<=n; i++)
{
fa[i] = i;
size[i] = 1;
}
维护到祖宗节点距离的并查集
例题:提高题库 167.信息传递
const int maxn = 200010;
int n = 0;
//fa[]存储每个点的祖宗节点, d[]存储x到fa[x]的距离
int fa[maxn] = {}, d[maxn] = {};
//返回x的祖宗节点
int findset(int x)
{
if(fa[x] != x)
{
int y = findset(fa[x]);
d[x] += d[fa[x]];
fa[x] = y;
}
return fa[x];
}
//将y所在集合合并到x集合
void merge(int x, int y)
{
int fx = findset(x), fy = findset(y);
if(fx != fy)
{
fa[fy] = fx;
d[fy] = d[x] + 1;
}
}
// 初始化,假定节点编号是1~n
for(int i=1; i<=n; i++) fa[i] = i;
树状数组
单点修改,区间查询
例题:提高题库 232.数列操作
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n = 0, m = 0;
int c[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while(x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
int getsum(int x)
{
int res = 0;
while(x)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
char op[5];
int a = 0, b = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a);
add(i, a);
}
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &a, &b);
if(op[0] == 'S') //区间查询
{
printf("%d\n", getsum(b) - getsum(a-1));
}
else //单点修改
{
add(a, b);
}
}
return 0;
}
区间修改,单点查询
例题:提高题库 210 数列操作b
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n = 0, m = 0;
int a[maxn] = {}, c[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
while(x <= n)
{
c[x] += val;
x += lowbit(x);
}
}
int getsum(int x)
{
int res = 0;
while(x)
{
res += c[x];
x -= lowbit(x);
}
return res;
}
int main()
{
char op[5];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'Q') //单点查询
{
scanf("%d", &x);
printf("%d\n", getsum(x) + a[x]);
}
else //区间修改
{
scanf("%d%d%d", &x, &y, &z);
add(x, z);
add(y+1, -z);
}
}
return 0;
}
区间修改,区间查询
例题:提高题库 235 数列操作c
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100010;
int n = 0, m = 0;
int a[maxn] = {};
ll c1[maxn] = {}, c2[maxn] = {};
int lowbit(int x)
{
return x & -x;
}
void add(int x, int val)
{
ll val2 = 1ll * val * x;
while(x <= n)
{
c1[x] += val;
c2[x] += val2;
x += lowbit(x);
}
}
ll getsum1(int x)
{
ll res = 0;
while(x)
{
res += c1[x];
x -= lowbit(x);
}
return res;
}
ll getsum2(int x)
{
ll res = 0;
while(x)
{
res += c2[x];
x -= lowbit(x);
}
return res;
}
ll getsum(int l, int r)
{
ll res1 = getsum1(r) * (r + 1) - getsum1(l-1) * l;
ll res2 = getsum2(r) - getsum2(l-1);
return res1 - res2;
}
int main()
{
char op[5];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=n; i>=2; i--) a[i] = a[i] - a[i-1];
for(int i=1; i<=n; i++) add(i, a[i]);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'A') //区间修改
{
scanf("%d%d%d", &x, &y, &z);
add(x, z);
add(y+1, -z);
}
else //区间查询
{
scanf("%d%d", &x, &y);
printf("%lld\n", getsum(x, y));
}
}
return 0;
}
二维树状数组
单点修改,区间查询
例题:提高题库 201.移动电话
#include <bits/stdc++.h>
using namespace std;
//二维树状数组板子题
const int maxn = 1050;
int n = 0;
int a[maxn][maxn] = {}, c[maxn][maxn] = {};
int lowbit(int x)
{
return x & (-x);
}
//单点加
//修改(x, y)这个点的值
void add(int x, int y, int val)
{
for(int i=x; i<=n; i+=lowbit(i))
{
for(int j=y; j<=n; j+=lowbit(j))
{
c[i][j] += val;
}
}
}
//求(0, 0)到(x, y)之间矩阵的和
int getsum(int x, int y)
{
int res = 0;
for(int i=x; i>0; i-=lowbit(i))
{
for(int j=y; j>0; j-=lowbit(j))
{
res += c[i][j];
}
}
return res;
}
//求子矩阵和,子矩阵x满足l<=x<=r,子矩阵y满足b<=y<=t
int sum(int l, int b, int r, int t)
{
int res = 0;
res = getsum(r, t) - getsum(l-1, t) - getsum(r, b-1) + getsum(l-1, b-1);
return res;
}
int main()
{
int op = 0;
int x = 0, y = 0, val = 0;
int l = 0, b = 0, r = 0, t = 0;
scanf("%d%d", &op, &n);
while(1)
{
scanf("%d", &op);
if(op == 3) break;
else if(op == 1)
{
scanf("%d%d%d", &x, &y, &val);
add(x+1, y+1, val);
}
else if(op == 2)
{
scanf("%d%d%d%d", &l, &b, &r, &t);
int res = sum(l+1, b+1, r+1, t+1);
printf("%d\n", res);
}
}
return 0;
}
线段树
单点修改,区间查询
例题:提高题库 232.数列操作
#include <bits/stdc++.h>
using namespace std;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r, sum;
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int pos, int val)
{
if(tree[rt].l == tree[rt].r) //找到对应的叶子节点
{
tree[rt].sum += val;
return;
}
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(pos <= mid) Update(lson, pos, val);
else Update(rson, pos, val);
pushup(rt);
}
//当前节点为rt,要查询的区间是[l, r]
int Query(int rt, int l, int r)
{
//如果节点表示的区间是查询区间的真子集
if(l<=tree[rt].l && tree[rt].r<=r)
{
return tree[rt].sum;
}
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(r <= mid) return Query(lson, l, r);
else if(l > mid) return Query(rson, l, r);
else return Query(lson, l, r) + Query(rson, l, r);
}
int main()
{
char op[5];
int x = 0, y = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &x, &y);
if(op[0] == 'S')
{
printf("%d\n", Query(1, x, y));
}
else
{
Update(1, x, y);
}
}
return 0;
}
区间修改,单点查询
例题:提高题库 210 数列操作b
#include <bits/stdc++.h>
using namespace std;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r, sum;
int lazy; //延迟标记
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
if(tree[rt].lazy) //此节点有延迟标记
{
int lz = tree[rt].lazy;
tree[rt].lazy = 0; //记住要清零
tree[lson].lazy += lz;
tree[rson].lazy += lz;
tree[lson].sum += lz * (tree[lson].r - tree[lson].l + 1);
tree[rson].sum += lz * (tree[rson].r - tree[rson].l + 1);
}
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int l, int r, int val)
{
//更新区间完全覆盖节点表示的区间
if(l<=tree[rt].l && tree[rt].r<=r)
{
tree[rt].lazy += val;
tree[rt].sum += val * (tree[rt].r - tree[rt].l + 1);
return;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(l <= mid) Update(lson, l, r, val);
if(r > mid) Update(rson, l, r, val);
pushup(rt);
}
//当前节点为rt,要查询的区间是[l, r]
int Query(int rt, int l, int r)
{
//如果节点表示的区间是查询区间的真子集
if(l<=tree[rt].l && tree[rt].r<=r)
{
return tree[rt].sum;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(r <= mid) return Query(lson, l, r);
else if(l > mid) return Query(rson, l, r);
else return Query(lson, l, r) + Query(rson, l, r);
}
int main()
{
char op[10];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'Q')
{
scanf("%d", &x);
printf("%d\n", Query(1, x, x));
}
else
{
scanf("%d%d%d", &x, &y, &z);
Update(1, x, y, z);
}
}
return 0;
}
区间修改,区间查询
例题:提高题库 235 数列操作c
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//预编译命令,做符号代换
#define lson (rt << 1)
#define rson (rt << 1 | 1)
const int maxn = 1e5 + 10;
int n = 0, m = 0;
struct node
{
int l, r;
ll sum;
int lazy; //延迟标记
}tree[maxn << 2];
int a[maxn] = {};
void pushup(int rt)
{
tree[rt].sum = tree[lson].sum + tree[rson].sum;
}
//把当前节点rt的延迟标记下放到左右儿子
void pushdown(int rt)
{
if(tree[rt].lazy) //此节点有延迟标记
{
int lz = tree[rt].lazy;
tree[rt].lazy = 0; //记住要清零
tree[lson].lazy += lz;
tree[rson].lazy += lz;
tree[lson].sum += lz * (tree[lson].r - tree[lson].l + 1);
tree[rson].sum += lz * (tree[rson].r - tree[rson].l + 1);
}
}
//建树
void Build(int rt, int l, int r)
{
tree[rt].l = l;
tree[rt].r = r; //节点信息初始化
if(l == r) //到叶节点
{
tree[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson, l, mid);
Build(rson, mid+1, r);
//子树建好后,回溯时更新父节点信息
pushup(rt);
}
void Update(int rt, int l, int r, int val)
{
//更新区间完全覆盖节点表示的区间
if(l<=tree[rt].l && tree[rt].r<=r)
{
tree[rt].lazy += val;
tree[rt].sum += val * (tree[rt].r - tree[rt].l + 1);
return;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(l <= mid) Update(lson, l, r, val);
if(r > mid) Update(rson, l, r, val);
pushup(rt);
}
//当前节点为rt,要查询的区间是[l, r]
long long Query(int rt, int l, int r)
{
//如果节点表示的区间是查询区间的真子集
if(l<=tree[rt].l && tree[rt].r<=r)
{
return tree[rt].sum;
}
//如果不能完全覆盖,此时需要向下递归,要下放标记
pushdown(rt);
int mid = (tree[rt].l + tree[rt].r) >> 1;
if(r <= mid) return Query(lson, l, r);
else if(l > mid) return Query(rson, l, r);
else return Query(lson, l, r) + Query(rson, l, r);
}
int main()
{
char op[10];
int x = 0, y = 0, z = 0;
scanf("%d", &n);
if(n == 0) return 0;
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
Build(1, 1, n);
scanf("%d", &m);
for(int i=1; i<=m; i++)
{
scanf("%s", op);
if(op[0] == 'S')
{
scanf("%d%d", &x, &y);
printf("%lld\n", Query(1, x, y));
}
else
{
scanf("%d%d%d", &x, &y, &z);
Update(1, x, y, z);
}
}
return 0;
}
动态开点
例题:提高题库 2009.Promotion Counting
#include <bits/stdc++.h>
using namespace std;
#define lson tree[rt].ls
#define rson tree[rt].rs
const int maxn = 1e5 + 10;
int n = 0, len = 0; //n为原始长度,len为离散化后的长度
int a[maxn] = {}, b[maxn] = {};
//邻接链表存图
int h[maxn] = {}, to[maxn] = {}, nxt[maxn] = {}, tot = 0;
//线段树变量
int root[maxn] = {}, segtot = 0;
//为树的每个节点建立一棵权值线段树
//每个权值线段树只标记一个值,需要log(maxn)个点,log(maxn)≈17
//最多共有maxn个点,因此tree开20*maxn
struct node
{
int ls, rs, cnt;
}tree[20*maxn];
//存储答案
int ans[maxn] = {};
void addedge(int x, int y)
{
to[++tot] = y;
nxt[tot] = h[x];
h[x] = tot;
}
//权值线段树加点
void update(int &rt, int l, int r, int pos, int val)
{
if(!rt) rt = ++segtot;
if(l == r)
{
tree[rt].cnt += val;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) update(lson, l, mid, pos, val);
else update(rson, mid+1, r, pos, val);
tree[rt].cnt = tree[lson].cnt + tree[rson].cnt;
}
//线段树合并
int segmerge(int ra, int rb)
{
if(!ra) return rb;
if(!rb) return ra;
tree[ra].cnt += tree[rb].cnt;
tree[ra].ls = segmerge(tree[ra].ls, tree[rb].ls);
tree[ra].rs = segmerge(tree[ra].rs, tree[rb].rs);
return ra;
}
//查询以rt为根节点的权值线段树值域为[x,y]的值
int query(int rt, int l, int r, int x, int y)
{
if(!rt) return 0;
if(l>=x && r<=y) return tree[rt].cnt;
int ans = 0;
int mid = (l + r) >> 1;
if(x <= mid) ans += query(lson, l, mid, x, y);
if(y > mid) ans += query(rson, mid+1, r, x, y);
return ans;
}
//遍历整棵树,并不断将子树合并到父节点
void dfs(int x)
{
for(int i=h[x]; i; i=nxt[i])
{
int y = to[i];
dfs(y);
root[x] = segmerge(root[x], root[y]);
}
ans[x] = query(root[x], 1, len, a[x]+1, maxn);
}
int main()
{
int x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i];
}
//离散化
sort(b+1, b+1+n);
len = unique(b+1, b+1+n) - (b+1);
for(int i=1; i<=n; i++)
{
a[i] = lower_bound(b+1, b+1+n, a[i]) - b;
update(root[i], 1, len, a[i], 1);
}
//读边
for(int i=2; i<=n; i++)
{
scanf("%d", &x);
addedge(x, i);
}
dfs(1);
for(int i=1; i<=n; i++) printf("%d\n", ans[i]);
return 0;
}
单调队列
例题
例题:249.窗口
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
int n = 0, k = 0;
int a[maxn] = {};
deque<int> q; //双端队列
int main()
{
scanf("%d%d", &n, &k);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
//求最小值,单调递减队列
for(int i=1; i<=n; i++)
{
if(i>k && q.front()==i-k) q.pop_front(); //越界元素出队
while(q.size() && a[q.back()]>a[i]) q.pop_back(); //将队尾不合法元素出队
q.push_back(i);
if(i >= k) printf("%d ", a[q.front()]);
}
printf("\n");
while(q.size()) q.pop_front(); //清空队列
//求最大值,单调递增队列
for(int i=1; i<=n; i++)
{
if(i>k && q.front()==i-k) q.pop_front(); //越界元素出队
while(q.size() && a[q.back()]<a[i]) q.pop_back(); //将队尾不合法元素出队
q.push_back(i);
if(i >= k) printf("%d ", a[q.front()]);
}
return 0;
}
ST算法
例题
例题:346.均衡队形
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
int n = 0, q = 0;
int a[maxn] = {}, f[maxn][30] = {}, g[maxn][30] = {};
//ST算法求最大值
int getmax(int l, int r)
{
int k = log2(r - l + 1);
return max(f[l][k], f[r-(1<<k)+1][k]);
}
//ST算法求最小值
int getmin(int l, int r)
{
int k = log2(r - l + 1);
return min(g[l][k], g[r-(1<<k)+1][k]);
}
int main()
{
scanf("%d%d", &n, &q);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
f[i][0] = g[i][0] = a[i];
}
//ST算法初始化
int t = log2(n) + 1;
for(int j=1; j<t; j++)
{
for(int i=1; i+(1<<j)-1<=n; i++)
{
f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
g[i][j] = min(g[i][j-1], g[i+(1<<(j-1))][j-1]);
}
}
int x = 0, y = 0;
for(int i=1; i<=q; i++)
{
scanf("%d%d", &x, &y);
printf("%d\n", getmax(x, y) - getmin(x, y));
}
return 0;
}
哈希
一般哈希
拉链法
//mod为超过最大范围的第一个质数(可以避免重复,数学上有证明)
int h[mod], e[mod], ne[mod], idx;
// 向哈希表中插入一个数
void insert(int x)
{
int k = (x % mod + mod) % mod;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % mod + mod) % mod; //此处是为了转化为正数
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
开放寻址法
int h[mod];
// 如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x)
{
int t = (x % mod + mod) % mod;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == mod) t = 0;
}
return t;
}
例题
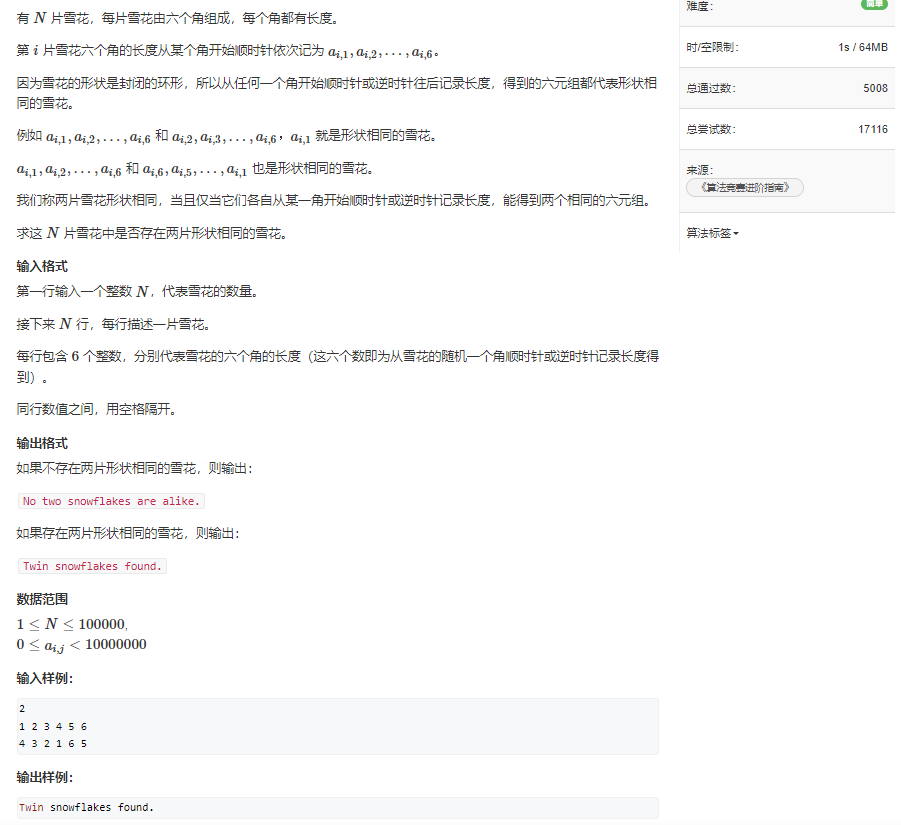
acwing137 雪花
//拉链法
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100010;
const int mod = 99991;
int n = 0;
int a[10] = {};
int snow[maxn][6] = {}, h[maxn] = {}, nxt[maxn] = {}, tot = 0;
//计算哈希值
int ha(int a[])
{
int sum = 0, mul = 1;
for(int i=0; i<6; i++)
{
sum = (sum + a[i]) % mod;
mul = (long long)mul * a[i] % mod;
}
return (sum + mul) % mod;
}
bool equal(int a[], int b[])
{
for(int i=0; i<6; i++)
{
for(int j=0; j<6; j++)
{
//相同方向比较
bool flag = true;
for(int k=0; k<6; k++)
{
if(a[(i+k)%6] != b[(j+k)%6])
{
flag = false;
break;
}
}
if(flag) return true;
//相反方向比较
flag = true;
for(int k=0; k<6; k++)
{
if(a[(i+k)%6] != b[(j-k+6)%6])
{
flag = false;
break;
}
}
if(flag) return true;
}
}
return false;
}
bool insert(int a[])
{
int val = ha(a);
//遍历表头h[val]指向的链表,寻找形状相同的雪花
for(int i=h[val]; i; i=nxt[i])
{
if(equal(snow[i], a)) return true;
}
//未找到形状相同的雪花,执行插入
++tot;
memcpy(snow[tot], a, 6 * sizeof(int));
nxt[tot] = h[val];
h[val] = tot;
return false;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
for(int j=0; j<6; j++) scanf("%d", &a[j]);
if(insert(a))
{
printf("Twin snowflakes found.");
return 0;
}
}
printf("No two snowflakes are alike.");
return 0;
}
//开放寻址法
#include <bits/stdc++.h>
using namespace std;
const int maxn = 200010;
const int mod = 200003;
int n = 0;
int a[10] = {};
int snow[maxn][6] = {}, h[maxn] = {};
//计算哈希值
int ha(int a[])
{
int sum = 0, mul = 1;
for(int i=0; i<6; i++)
{
sum = (sum + a[i]) % mod;
mul = (long long)mul * a[i] % mod;
}
return (sum + mul) % mod;
}
bool equal(int a[], int b[])
{
for(int i=0; i<6; i++)
{
for(int j=0; j<6; j++)
{
//相同方向比较
bool flag = true;
for(int k=0; k<6; k++)
{
if(a[(i+k)%6] != b[(j+k)%6])
{
flag = false;
break;
}
}
if(flag) return true;
//相反方向比较
flag = true;
for(int k=0; k<6; k++)
{
if(a[(i+k)%6] != b[(j-k+6)%6])
{
flag = false;
break;
}
}
if(flag) return true;
}
}
return false;
}
int find(int a[])
{
int val = ha(a);
//遍历表头h[val]指向的链表,寻找形状相同的雪花
while(h[val] && !equal(snow[val], a))
{
val++;
if(val == mod) val = 0;
}
return val;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
for(int j=0; j<6; j++) scanf("%d", &a[j]);
int k = find(a);
if(h[k])
{
printf("Twin snowflakes found.");
return 0;
}
memcpy(snow[k], a, 6 * sizeof(int));
h[k] = 1;
}
printf("No two snowflakes are alike.");
return 0;
}
字符串哈希
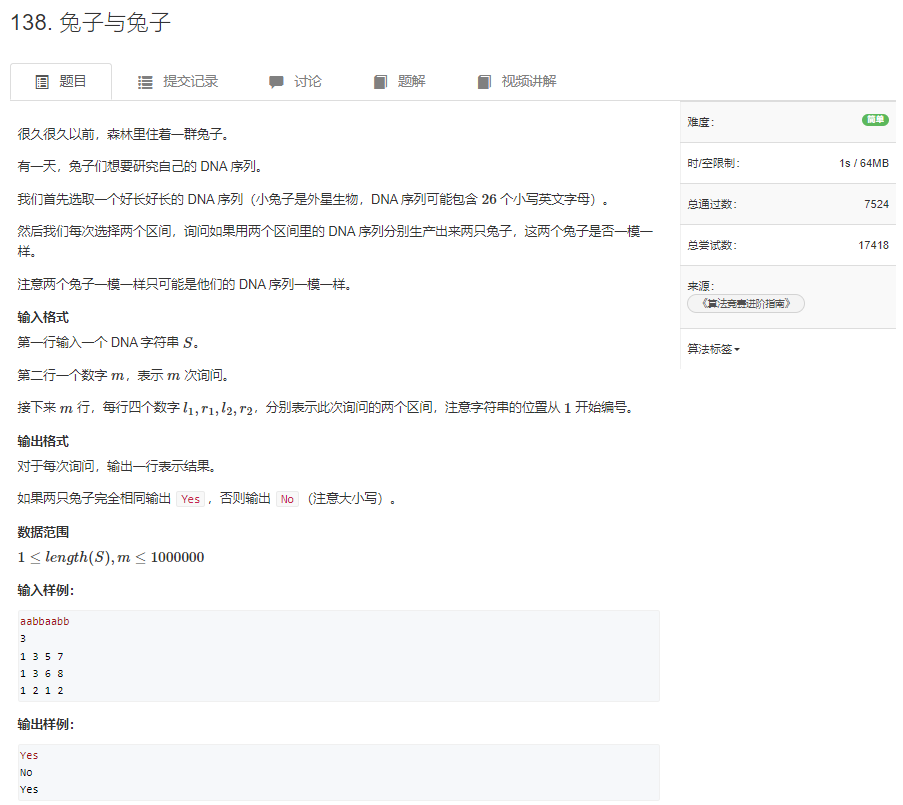
acwing138 兔子
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int maxn = 1000010;
const int mod = 131;
int n = 0, q = 0;
char s[maxn] = {};
ull f[maxn] = {}, p[maxn] = {};
int main()
{
scanf("%s", s + 1);
n = strlen(s + 1);
scanf("%d", &q);
p[0] = 1;
for(int i=1; i<=n; i++)
{
f[i] = f[i-1] * mod + (s[i] - 'a' + 1); //前缀和哈希
p[i] = p[i-1] * mod;
}
for(int i=1; i<=q; i++)
{
int l1 = 0, r1 = 0, l2 = 0, r2 = 0;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
if(f[r1] - f[l1-1] * p[r1-l1+1] == f[r2] - f[l2-1] * p[r2-l2+1])
{
printf("Yes\n");
}
else printf("No\n");
}
return 0;
}
分块/莫队
莫队算法都是离线算法
分块例题
例题: 5939.一个简单的整数问题
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
int n = 0, m = 0;
int a[maxn] = {};
//L[i]和R[i]表示第i段的左右端点,pos[i]表示a序列中的第i个位置的数位于第几段
//cnt表示分成的段数
int L[400] = {}, R[400] = {}, pos[maxn] = {}, cnt;
ll sum[400] = {}, add[400] = {};
//分块
void init()
{
cnt = sqrt(n);
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * cnt + 1;
R[i] = i * cnt;
}
//分出sqrt(n)块后,还有剩余的部分,单独再分一块
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
//预处理pos和sum
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
sum[i] += a[j];
}
}
}
ll Query(int l, int r)
{
ll ans = 0;
int p = pos[l], q = pos[r];
if(p == q)//l~r处于同一分块中
{
for(int i=l; i<=r; i++) ans += a[i];
ans += (r - l + 1) * add[p];
}
else
{
//先处理整块数据
for(int i=p+1; i<q; i++)
{
ans += sum[i] + add[i] * (R[i] - L[i] + 1);
}
//处理最左边块
for(int i=l; i<=R[p]; i++) ans += a[i];
ans += (R[p] - l + 1) * add[p];
//处理最右边块
for(int i=L[q]; i<=r; i++) ans += a[i];
ans += (r - L[q] + 1) * add[q];
}
return ans;
}
void Update(int l, int r, int d)
{
int p = pos[l], q = pos[r];
if(p == q)//l~r处于同一分块中
{
for(int i=l; i<=r; i++) a[i] += d;
sum[p] += d * (r - l + 1);
}
else
{
//先处理整块数据
for(int i=p+1; i<q; i++) add[i] += d;
//处理最左边块
for(int i=l; i<=R[p]; i++) a[i] += d;
sum[p] += d * (R[p] - l + 1);
//处理最右边块
for(int i=L[q]; i<=r; i++) a[i] += d;
sum[q] += d * (r - L[q] + 1);
}
}
int main()
{
char op[3] = {};
int l = 0, r = 0, d = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
init();
//指令
while(m--)
{
scanf("%s", op);
if(op[0] == 'Q')
{
scanf("%d%d", &l, &r);
ll ans = Query(l, r);
printf("%lld\n", ans);
}
else
{
scanf("%d%d%d", &l, &r, &d);
Update(l, r, d);
}
}
return 0;
}
莫队朴素版
例题: 1648.HH的项链
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxx = 1e6+10;
int n = 0, m = 0;
int a[maxn] = {};
int l = 1, r = 0, cnt[maxx] = {}, ans = 0;
void add(int x)
{
if(cnt[x] == 0) ans++;
cnt[x]++;
}
void del(int x)
{
cnt[x]--;
if(cnt[x] == 0) ans--;
}
int main()
{
int x = 0, y = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
scanf("%d", &m);
while(m--)
{
scanf("%d%d", &x, &y);
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
printf("%d\n", ans);
}
return 0;
}
莫队奇偶排序版

例题: 1648.HH的项链
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxx = 1e6+10;
const int maxm = 2e5 + 10;
int n = 0, m = 0;
int a[maxn] = {};
//莫队信息
int l = 1, r = 0, col[maxx] = {}, num = 0, ans[maxm] = {};
//分块信息
int L[maxn] = {}, R[maxn] = {}, pos[maxn] = {}, cnt = 0;
struct node
{
int x, y, id;
}q[maxm];
//奇偶排序
//左端点按所在块,由小到大排序
//奇数块时右端点由小到大,偶数块右端点由大到小
//奇偶排序可以做到上一块r由~n,该块r由n~1
bool cmp(node &nd1, node &nd2)
{
int p = pos[nd1.x], q = pos[nd2.x];
if(p != q) return p < q;
if(p & 1 == 1) return nd1.y < nd2.y;
else return nd1.y > nd2.y;
}
void init()
{
//当块的大小取n/sqrt(m)时,时间复杂度可以达到最优
int B = n / sqrt(m);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = B * (i - 1) + 1;
R[i] = B * i;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
void add(int x)
{
if(col[x] == 0) num++;
col[x]++;
}
void del(int x)
{
col[x]--;
if(col[x] == 0) num--;
}
int main()
{
int x = 0, y = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
//分块
scanf("%d", &m);
init();
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
q[i] = { x, y, i };
}
sort(q+1, q+1+m, cmp);
for(int i=1; i<=m; i++)
{
x = q[i].x;
y = q[i].y;
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
ans[q[i].id] = num;
}
for(int i=1; i<=m; i++) printf("%d\n", ans[i]);
return 0;
}
带修莫队
例题: 350.数颜色
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10010;
const int maxx = 1e6+10;
int n = 0, m = 0;
int a[maxn] = {};
int l = 1, r = 0, cnt[maxx] = {}, ans = 0;
void add(int x)
{
if(cnt[x] == 0) ans++;
cnt[x]++;
}
void del(int x)
{
cnt[x]--;
if(cnt[x] == 0) ans--;
}
int main()
{
char op[3] = {};
int x = 0, y = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
while(m--)
{
scanf("%s%d%d", op, &x, &y);
if(op[0] == 'Q')
{
//莫队算法
while(x<l) { l--; add(a[l]); }
while(x>l) { del(a[l]); l++; }
while(y<r) { del(a[r]); r--; }
while(y>r) { r++; add(a[r]); }
printf("%d\n", ans);
}
else
{
if(x>=l && x<=r)
{
del(a[x]);
add(y);
}
a[x] = y;
}
}
return 0;
}
例题: 351.维护队列



#include <bits/stdc++.h>
using namespace std;
const int maxn = 150010;
const int maxx = 1e6+10;
const int maxm = 150010;
//带修莫队,相当于在朴素莫队的基础上,增加了一维,表示时间
//在完成朴素莫队更新后,还要判断修改时间,将修改时间更新到正确位置
int n = 0, m = 0;
int a[maxn] = {};
//莫队数据
int l = 1, r = 0, t = 0, col[maxx] = {}, num = 0, ans[maxm] = {};
//分块数据
int L[500] = {}, R[500] = {}, pos[maxn] = {}, cnt = 0;
struct node1
{
//t表示该询问位于第几次修改
int id, l, r, t;
}q[maxm] = {};
//存储修改信息
struct node2
{
int x, c;
}rp[maxm] = {};
bool cmp(const node1 &nd1, const node1 &nd2)
{
//先按左端点所在块升序
//左端点块相同按右端点所在块升序
//左右端点块相同,按t升序
int p = pos[nd1.l], q = pos[nd2.l];
if(p != q) return p < q;
p = pos[nd1.r], q = pos[nd2.r];
if(p != q) return p < q;
return nd1.t < nd2.t;
}
//分块
void init()
{
int B = pow(n, 0.666);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * B + 1;
R[i] = i * B;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
//朴素莫队加
void add(int x)
{
if(col[x] == 0) num++;
col[x]++;
}
//朴素莫队减
void del(int x)
{
col[x]--;
if(col[x] == 0) num--;
}
int main()
{
char op[3] = {};
int x = 0, y = 0;
int mq = 0, mr = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
for(int i=1; i<=m; i++)
{
scanf("%s%d%d", op, &x, &y);
if(op[0] == 'Q') //单独记录查询的信息
{
mq++;
q[mq] = { mq, x, y, mr };
}
else //单独记录修改的信息
{
mr++;
rp[mr] = { x, y };
}
}
init();
sort(q+1, q+1+mq, cmp);
for(int i=1; i<=mq; i++)
{
//朴素莫队操作
while(q[i].l<l) { l--; add(a[l]); }
while(q[i].l>l) { del(a[l]); l++; }
while(q[i].r<r) { del(a[r]); r--; }
while(q[i].r>r) { r++; add(a[r]); }
//更新时间t这一维
while(q[i].t<t)
{
//修改的数据位于[l,r]之间,则需要更新,否则不需要更新
if(rp[t].x>=l && rp[t].x<=r)
{
del(a[rp[t].x]);
add(rp[t].c);
}
//注意这里是交换值,不是直接更改a数组,因为后面还要回滚
swap(a[rp[t].x], rp[t].c);
t--;
}
while(q[i].t>t)
{
t++;
if(rp[t].x>=l && rp[t].x<=r)
{
del(a[rp[t].x]);
add(rp[t].c);
}
swap(a[rp[t].x], rp[t].c);
}
ans[q[i].id] = num;
}
for(int i=1; i<=mq; i++) printf("%d\n", ans[i]);
return 0;
}
回滚莫队
例题: 605 permu
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50010;
const int maxm = 50010;
int n = 0, m = 0;
int a[maxn] = {};
//分块信息
int L[300] = {}, R[300] = {}, pos[maxn] = {}, cnt = 0;
struct node
{
int id, l, r;
}q[maxm];
//ls[x]和rs[x]分别表示x点向左向右延伸距离
//backls, backrs用于后面的回滚
int ls[maxn] = {}, rs[maxn] = {}, backls[maxn] = {}, backrs[maxn] = {}, num = 0, ans[maxm] = {};
bool cmp(const node &nd1, const node &nd2)
{
int p = pos[nd1.l], q = pos[nd2.l];
if(p != q) return p < q;
return nd1.r < nd2.r;
}
void init()
{
int B = sqrt(n);
cnt = n / B;
for(int i=1; i<=cnt; i++)
{
L[i] = (i-1) * B + 1;
R[i] = i * B;
}
if(R[cnt] < n)
{
cnt++;
L[cnt] = R[cnt-1] + 1;
R[cnt] = n;
}
for(int i=1; i<=cnt; i++)
{
for(int j=L[i]; j<=R[i]; j++)
{
pos[j] = i;
}
}
}
void add(int x)
{
//更新x这个点的左右延伸距离
//如果x在某个连续区间的中间位置,可能会出现左延伸或右延伸不能更新,这种情况不影响答案
//因为我们求的是最大连续区间,所以只要保证当x为连续区间边界的点时,能够更新就可以
//因此,后面我们要更新rs[x-ls[x]+1]和ls[x+rs[x]-1]的值
ls[x] = ls[x-1] + 1; //左边延伸+1
rs[x] = rs[x+1] + 1; //右边延伸+1;
int t = ls[x] + rs[x] - 1;
//更新该连续区间左右端点的延伸距离
rs[x-ls[x]+1] = t;
ls[x+rs[x]-1] = t;
num = max(num, t);
}
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
}
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
q[i] = { i, x, y };
}
init();
sort(q+1, q+1+m, cmp);
for(int i=1; i<=m; )
{
int j = i;
while(j<=m && pos[q[i].l] == pos[q[j].l]) j++;
int right = R[pos[q[i].l]];
//块内移动,直接暴力
while(i<j && q[i].r<=right)
{
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
int id = q[i].id, l = q[i].l, r = q[i].r;
for(int k=l; k<=r; k++) add(a[k]);
ans[q[i].id] = num;
i++;
}
//块外移动
//r设置为q[i].l所在块终点位置,然后向右移动
//l设置为r+1,即q[i].l所在块的下一个块的起始位置,以保证初始空间为0,然后向左移动
//r的轨迹会一直往后移(前面对q的排序)
//l会在q[i].l中不断来回移动
//每次求出一个询问后,回滚到l的起始位置
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
int r = right, l = right + 1;
while(i < j)
{
//先向右扩展
while(r < q[i].r) { r++; add(a[r]); }
//先备份下来,以便后面回滚,然后再向左扩展
int backup = num;
memcpy(backls, ls, sizeof(ls));
memcpy(backrs, rs, sizeof(rs));
while(l > q[i].l) { l--; add(a[l]); }
ans[q[i].id] = num;
//回滚
l = right + 1;
num = backup;
memcpy(ls, backls, sizeof(ls));
memcpy(rs, backrs, sizeof(rs));
i++;
}
num = 0;
memset(ls, 0, sizeof(ls));
memset(rs, 0, sizeof(rs));
}
for(int i=1; i<=m; i++) printf("%d\n", ans[i]);
return 0;
}
平衡树
splay
#include <bits/stdc++.h>
using namespace std;
const int maxn = 100005;
//rt:根节点编号,tot:节点个数,fa[i]:父亲
//ch[i][0]左儿子编号,ch[i][1]右儿子编号
//val[i]节点权值,cnt[i]权值出现次数,sz[i]子树大小
int rt, tot, fa[maxn], ch[maxn][2], val[maxn], cnt[maxn], sz[maxn];
struct Splay
{
//在改变节点位置后,将节点x的size更新
void maintain(int x)
{
sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x];
}
//判断节点x是父亲节点的左儿子还是右儿子
//左儿子返回false,右儿子返回true
bool get(int x)
{
return x == ch[fa[x]][1];
}
//销毁节点x
void clear(int x)
{
ch[x][0] = ch[x][1] = fa[x] = val[x] = cnt[x] = 0;
}
//为了使splay保持平衡而进行旋转操作,
//旋转的本质是将某个节点上移一个位置
void rotate(int x)
{
int y = fa[x], z = fa[y], chk = get(x);
ch[y][chk] = ch[x][chk^1];
if(ch[x][chk^1]) fa[ch[x][chk^1]] = y;
ch[x][chk^1] = y;
fa[y] = x;
fa[x] = z;
if(z) ch[z][y==ch[z][1]] = x;
maintain(y);
maintain(x);
}
void splay(int x)
{
for(int f=fa[x]; f=fa[x], f; rotate(x))
{
if(fa[f])
{
rotate(get(x) == get(f) ? f : x);
}
}
rt = x;
}
void ins(int k)
{
if(!rt)
{
val[++tot] = k;
cnt[tot]++;
rt = tot;
maintain(rt);
return;
}
int cur = rt, f = 0;
while(1)
{
if(val[cur] == k)
{
cnt[cur]++;
maintain(cur);
maintain(f);
splay(cur);
break;
}
f = cur;
cur = ch[cur][val[cur] < k];
if(!cur)
{
val[++tot] = k;
cnt[tot]++;
fa[tot] = f;
ch[f][val[f] < k] = tot;
maintain(tot);
maintain(f);
splay(tot);
break;
}
}
}
//查询 x 的排名
int rk(int k)
{
int res = 0, cur = rt;
while(1)
{
if(k < val[cur])
{
cur = ch[cur][0];
}
else
{
res += sz[ch[cur][0]];
if(!cur) return res + 1;
if(k == val[cur])
{
splay(cur);
return res + 1;
}
res += cnt[cur];
cur = ch[cur][1];
}
}
}
//查询排名 x 的数
int kth(int k)
{
int cur = rt;
while(1)
{
if(ch[cur][0] && k<=sz[ch[cur][0]])
{
cur = ch[cur][0];
}
else
{
k -= cnt[cur] + sz[ch[cur][0]];
if(k <= 0)
{
splay(cur);
return val[cur];
}
cur = ch[cur][1];
}
}
}
//将 x 插入(此时 x 已经在根的位置了),
//前驱即为 x 的左子树中最右边的节点,最后将 x 删除即可。
//在进行pre之前,先要ins(x)
int pre()
{
int cur = ch[rt][0];
if(!cur) return cur;
while(ch[cur][1]) cur = ch[cur][1];
splay(cur);
return cur;
}
int nxt()
{
int cur = ch[rt][1];
if(!cur) return cur;
while(ch[cur][0]) cur = ch[cur][0];
splay(cur);
return cur;
}
void del(int k)
{
rk(k);
if(cnt[rt] > 1)
{
cnt[rt]--;
maintain(rt);
return;
}
if(!ch[rt][0] && !ch[rt][1])
{
clear(rt);
rt = 0;
return;
}
if(!ch[rt][0])
{
int cur = rt;
rt = ch[rt][1];
fa[rt] = 0;
clear(cur);
return;
}
if(!ch[rt][1])
{
int cur = rt;
rt = ch[rt][0];
fa[rt] = 0;
clear(cur);
return;
}
int cur = rt;
int x = pre();
fa[ch[cur][1]] = x;
ch[x][1] = ch[cur][1];
clear(cur);
maintain(rt);
}
}tree;
int main()
{
int n = 0, opt = 0, x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d", &opt, &x);
if(opt == 1)
{
tree.ins(x);
}
else if(opt == 2)
{
tree.del(x);
}
else if(opt == 3)
{
printf("%d\n", tree.rk(x));
}
else if(opt == 4)
{
printf("%d\n", tree.kth(x));
}
else if(opt == 5)
{
tree.ins(x);
printf("%d\n", val[tree.pre()]);
tree.del(x);
}
else if(opt == 6)
{
tree.ins(x);
printf("%d\n", val[tree.nxt()]);
tree.del(x);
}
}
return 0;
}



