2024.8.2
A 小L的有向图
题意:给出 \(n\) 个点,\(m\) 条边,任意删去一些边,会有 \(2^m\) 种子图。定义一个图的价值为它的合法拓扑序个数,求这 \(2^m\) 种图的价值和,对 \(998244353\) 取模。\(n \le 22\)
数据范围一眼状压。设 \(f_S\) 表示处理点集为 \(S\) 时且集内有序的总价值,最终答案为 \(f_{2^n-1}\)
考虑转移:发现当我们增加一个新点时,它能在序列中插入的位置是在它儿子的前面。比如当前扫了 \(k\) 个它的儿子,那么它就有 \(k\) 条边和原点集相连,而每条边又可能被删去,所以每条边删和不删就会分别对应一种原点集已经算好的拓扑序种类,贡献是 \(2^k\) 倍,有转移:
B [NOIP2022] 逛公园
题意:给一个有向有环图,边权非负,求出有多少种从 \(1\) 到 \(n\) 的走法,使得每种走法的权值和不超过其最短路的权值和 \(+K\)。
\(30\) pts,\(k = 0\)
直接就是最短路计数,跑一遍 dijkstra 就行。
\(70\) pts,无 \(0\) 边
观察到 \(k\le50\),可以跑一个 \(O(km)\) 的 \(\text{dp}\)。
设 \(f_{u,j}\) 表示 \(dis(1,u) \le mindis(1,u) + j\) 的路径方案。
我们设从 \(p\) 到 \(now\) 有一条长度为 \(w\) 的边,将 \(f_{p,x}\) 转移到 \(f_{now,k}\)。
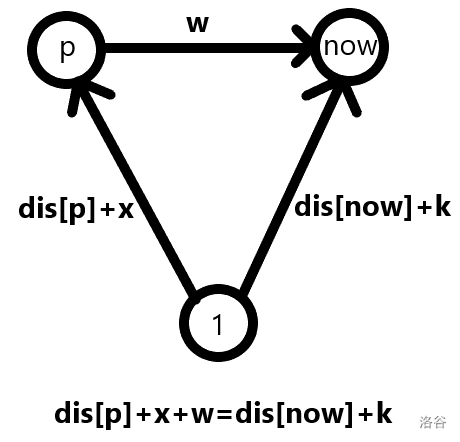
有: \(x-k = mindis(1,now)-mindis(1,p)-w\)
移项: \(x=mindis(1,now)-mindis(1,p)+k-w\)
最终有 \(f_{now,k} = (f_{now,k}+f_{p,x}) \mod P\)
C [NOIP2022] 建造军营
题意:给一个无向有环图,任选一个点集 \(V\),并保留一个边集 \(E\)(可为空),使得若从剩下的边中任意删掉一条,点集中的点两两可达,求方案数,对 \(10^9+7\) 取模。
35pts
\(n\le16\),考虑状压。显然状态为每个点取或不取,那么状态范围就是 \([1,2^n-1]\)。然后再对每个状态跑连通性搜索,如果所有点集内的点都被访问过,说明这个边是非桥边。统计每个状态下非桥边的个数 \(cnt\),答案就是 \(\sum2^{cnt}\)
特殊性质A:保证图为一条链
考虑在图中选取两点 \(l\) 和 \(r\),记为 \(V\) 的两个端点。
-
\(l=r\) 时,说明选了一个点。那么所有边都可删可留,\(n\) 种点选法,方案数 \(n2^{n-1}\)。
-
\(l \neq r\) 时,首先 \([1,l-1] \cup [r+1,n]\) 上的点所连边都可删可留,方案数 \(2^{n+l-r-1}\)。既然钦定 \(l,r\) 都可达,那么 \(V\) 中所有边都在 \(E\) 中,则 \([l+1,r-1]\) 的点可选可不选,方案 \(2^{r-l-1}\),每一个 \(l \neq r\) 的方案为 \(2^{(n+l-r-1)+(r-l-1)}=2^{n-2}\),发现只与 \(n\) 有关。然后考虑 \(l,r\) 的选法,有 \(\binom{n}{2}\) 种,即\(\frac{n(n-1)}{2}\),总方案为 \(n(n-1)2^{n-3}\)。
综上,答案为 \(n(2^{n-1}+(n-1)2^{n-3})\)
正解
容易发现,所有的非桥边都可以任意删除,不会影响图内连通性。
那么就可以进行边双缩点,把图缩成一棵树,桥边变成树边。设缩点后边数为 \(M\),那么就会有 \(m-M\) 个非桥边,那么答案便有了 \(2^{m-M}\) 的系数。
树上的连通性便容易了,当且仅当 \(s \sim t\) 的简单路径上所有边都在 \(E\) 中,\(s\) 和 \(t\) 联通。我们设 \(son_u\) 表示 \(u\) 的子树,\(e_u\) 表示 \(u\) 子树内所有边数,\(v\) 为 \(u\) 的一个子节点。
如果不在 \(son_v\) 内选点,那么 \((u,v)\) 这条边和 \(e_v\) 可选可不选,有 \(2^{e_v+1}\) 种方案。
如果在 \(son_v\) 内选点,那么需要分类讨论:
- 当 \(son_v\) 内存在点 \(x\) 使 \(x\) 和 \(v\) 需要通过非选边才能联通,那么我们无论选不选 \((u,v)\),\(x\) 和 \(u\) 不能连通。此时 \(u\) 以及更远的点,一定不能选,因为无法和 \(x\) 联通。
- 当 \(son_v\) 内不存在这样的点 \(x\),即所有 \(son_v\) 的点都和 \(v\) 通过选边连通,那么我们只要选择 \((u,v)\),\(son_v\) 里的所有选点都能和 \(u\) 联通,这时 \(u\),以及其他 \(v\) 同级的 \(u\) 的子节点子树内的点都能选了。
这两种情况必然会导致转移的差异,如果我们只用一个 \(f_v\) 必然无法转移,那么理应加一维来区分,但这里我们使用另一种方法。
设 \(f_u\) 表示 \(son_u\) 中至少选一个点,且选点全部能用选边与 \(u\) 联通。设 \(c_u\) 表示有 \(c_u\) 个点被缩进 \(u\) 这个点了,那么这些点可以随便选,所以答案有 \(2^{c_u}\) 的系数。
讨论 \(u\) 的子节点 \(v\) 及子树 \(son_v\)。
- \(son_v\) 不选点: \(son_v\) 上的边和 \((u,v)\) 这条边都可选或不选,\(2^{e_v+1}\)。
- \(son_v\) 选点:\((u,v)\) 必须选,就有 \(f_v\) 种情况。
而 \(f_u\) 需要保证 \(son_u\) 里必须选点,那么计算完毕后,会有 \(2^{e_u}\) 种不选点的选边情况
答案是 \(f_1\) 吗?不是,因为不一定所有选点都和根联通。我们应该计算的 \(u\) 的答案应该是点集 LCA 为 \(u\) 的方案,即在 \(f_u\) 中,\(u\) 没被选且只有一个子树选了点的方案,用 \(f_u\) 减去,乘上 \(2^{M-e_u}\)。
我们枚举 \(u\) 的子节点 \(v\),\(son_v\) 里有 \(f_v\) 种方案,\((u,v)\) 必选,\(son_u\) 中的其他边可选可不选,总共 \(f_v \cdot 2^{e_u-e_v-1}\) 种。
\(u\) 作为 \(\text{LCA}\) 对答案的贡献:
D [中山市选] 杀人游戏
题意:在有向图中有若干白点和一个黑点,每个点为黑点的概率均等。每次选择一个点发起询问,询问结果为该点和该点能直接到达的所有点的颜色
求出最优情况下,不对黑点发起询问且得知黑点编号的概率。
贪心地想,优先去找出度最多的点,只询问集团首领,那答案就是 $\frac{1}{n}num $。在无环的情况下,这样贪心几乎是正确的。但是本题有环,只能拿到 \(42\) 分。
那么考虑缩点,把强连通分量缩成一个点,将原图转化为 \(\text{DAG}\)。考虑这样一件事,如果我们查询了一个点有父亲,那么查父亲一定更优。为什么?因为如果你查了到了白点,你无法知道父亲是什么,所以必须要再向上查一次,这无疑会增大抽中黑点的概率。如果当前点是黑点,那么你会直接送掉,而如果你查了父亲,便会避免你的死亡,所以:如果一个点有向该点出边连接的点,查向它连接的点更优。
因此,我们在缩点后的新图中,对入度为 \(0\) 的点都查一次,如果都非黑,那么就成功了。猜测答案为 \(1-\frac{c}{n}\)(\(c\) 为入度为 \(0\) 的点个数)。
交一发:\(30\) 分!还没乱搞的贪心高。
考虑原图中一个 \(p\) 点,若它的入度为 \(0\),并且它可直接到达的点入度均 \(\ge 2\)(得保证还能有别的点访问到它),那么加入我们最后询问它,与它相连的其他所有颜色全都确定了。如果黑点在其他的 \(n-1\) 个点中,我们必然不用询问它;加入黑点还没有被发现,那么我们也不用询问它,因为已经确定它就是了。
因此:如果图中至少存在一个入度为 \(0\) 的 \(size = 1\) 的强联通分量,答案就会变成 \(1-\frac{c-1}{n}\)。
还要注意细节就是缩点之后边也得缩:本来一个强联通分量会连很多边,但是一个点就得化成一条了,得判重。
G [CSP-S 2022] 假期计划
首先暴力可以拿到 \(70\) 分。再考虑到当年线段树无脑搞 \(\text{T2}\) 就可以拿 \(65\),还有”不可以总司令“的 \(45\),纯暴力就可以搞到 \(180\) 了。
\(n \le 2500\),考虑 \(O(n^2)\)。我们需要在 \(O(n^2)\) 内求出全源最短路,那么我们跑 \(n\) 遍 SPFA 或者 dijkstra,进行最优性剪枝,并存下从每个点出发能 \(k\) 步到达且能 \(k\) 步回家的分值最大的三个地点。
接下来 \(n^2\) 枚举前中间 \(2\) 个景点,若这 \(2\)个中间景点可 \(k\) 步到达,再分别枚举他们的前三大可 \(k\) 步到达并 \(k\) 步回家的三个地点计算答案。一共 \(9\) 个,可记为常数,那么总复杂度就是 \(O(n^2)\) 了。


