2024.8.3
今天状态爆炸了,有几次差点睡着。\(\_ + 20+60+0\)
挂分
\(\text{T4}\) 的答案初值设的 \(2147483647\),但是答案超 \(int\) 了,导致丢掉暴力状压分。
方便 \(\text{dp}\) 的 \(\text{T4}\) 没写 \(\text{dp}\),没给 \(O(n^3)\) 分的 \(\text{T2}\) 却搞了好久 \(\text{dp}\)……
\(\text{T3}\) 的 \(m \le 3\) 写挂了。
T1 怎么又是先增后减(why)
题意:把给定序列进行相邻两数交换,求存在整数 \(k \in [1,n]\),满足该序列前 \(k\) 个数单调不降,后 \(n-k\) 个数单调不增的最小操作次数。
考场在吃 shit,这种结论题是一点都对不上脑电波。调了快一个半小时还是假的思路,果断放弃了。
考虑到序列是单峰的,小数往边放,大数往中间放。那么每一个数可以放到左半边也可以放到右半边,选一个近的位置放就行了。我们考虑从小到大换数,从序列中最小的数 \(i\) 开始。它必然要换到序列的最左端或最右端。那么它分别需要和左右两边所有比它大的数全换一遍(如果有数和它一样便不用换了,直接转移到那个数),就能换到两边,取左右两边的最小步数计入答案。将它从序列中踢出去,因为它已经到位了。这样,不断找到序列中的最小数,按照上面的步骤换,答案就算完了。
总结一下我们的过程,就是在左右两边找到比它大的数的个数,取最小值计入答案。那么我们便可以不用从小到大找数,直接从 \(1\) 到 \(n\) 扫一遍就行了。
接下来就是对于每一个 \(i\) ,怎么从 \(1\sim i-1\) 和 \(i+1 \sim n\) 中找到比 \(i\) 大的个数,上个树状数组/平衡树/权值线段树乱搞就行了,\(O(n\log n)\)。
const int N = 1e5+5;
int a[N];
mt19937 rnd(time(0));
struct TREE
{
struct NODE
{
int l,r,val,siz,key;
}tree[N<<2];
int cnt{},root{};
int newnode(int val){tree[++cnt].val = val; tree[cnt].siz =1,tree[cnt].key = rnd(); return cnt;}
void pushup(int x){tree[x].siz = tree[tree[x].l].siz + tree[tree[x].r].siz + 1;}
void split(int x,int val,int &l,int &r)
{
if(!x){ l = r = 0;return;}
if(tree[x].val <= val){l = x;split(tree[x].r,val,tree[x].r,r);pushup(x);}
else{r = x;split(tree[x].l,val,l,tree[x].l);pushup(x);}
}
int merge(int x,int y)
{
if(!x || !y) return x ^ y;
if(tree[x].key > tree[y].key){tree[x].r = merge(tree[x].r,y);pushup(x);return x;}
else{tree[y].l = merge(x,tree[y].l);pushup(y);return y;}
}
void ins(int val){int l,r;split(root,val,l,r);root = merge(l,merge(newnode(val),r));}
int nxt(int val){int l,r,ans;split(root,val,l,r);ans = tree[r].siz,root = merge(l,r);return ans;}
}tree,tree2;
int minn[N];
signed main()
{
#ifdef LOCAL
freopen("in.in","r",stdin);
#endif
int n = read();
for(int i{1};i<=n;i++)
{
a[i]= read();tree.ins(a[i]);
minn[i] = tree.nxt(a[i]);
}
int res{};
for(int i{n};i>=1;i--)
{
tree2.ins(a[i]);
minn[i] = min(minn[i],tree2.nxt(a[i]));
res += minn[i];
}
writeln(res);
return 0;
}
T2 美食节(festival)
题意:一个序列上有 \(N\) 个点,其中 \(\text{cjx}\) 最开始在 \(x\) 点,有 \(n\) 个区间按顺序给出, \(\text{cjx}\) 要依次进入这 \(n\) 个区间,定义花费为移动距离。\(\text{cjx}\) 每次都可以选择让 \(\text{wme}\) 帮他进入某次区间,花费不变但是他不必进入这个区间了。求这 \(n\) 个区间都被进入过后的最小花费。
显然要 \(\text{dp}\),诶就设 \(f_{i,j}\) 表示 \(\text{cjx}\) 在过第 \(i\) 个区间时在 \(j\) 这个位置的最小花费。一看数据范围:\(l,r \le 10^9\)。。那不急,\(n\le10^5\),那么关键点的数量必然不超过 \(2 \times 10^5+1\),离散化就行了。
那就设 \(f_{i,j}\) 表示 \(\text{cjx}\) 在过 \(i\) 个区间时在第 \(j\) 个关键点的最小花费。为什么是关键点,因为移动量小为优,确实只会在区间端点上停留。
他肯定有两种情况:
- 自己走一段(或者不走)到第 \(i\) 个区间的端点处。
- 自己走一段(或者不走),然后让 \(\text{wme}\) 帮他进区间。
显然的两种转移:
先跑一遍,大样例跑出来了,但是 \(O(n^3)\) 跑了 \(106s\),想了想不知道怎么优化,就先跳了。
但是这个题给 \(O(n^3)\) 放的分跟 \(O(n!),O(2^n)\) 的分一样。
现在再想想怎么优化,考虑到转移方程里有一个 \(dis(s,j)\) 这个东西由 \(s\) 和 \(j\) 两部分共同决定。由以前的经验,可以把它拆开预处理。因为 \(s\) 是 \(i-1\) 的,那么我们每一次在算完 \(f_i\) 的时候就去更新一下当前的 \(j\) ,到 \(i+1\) 的时候就能用上了。
当 \(s\) 在 \(j\) 左侧时,我们考虑怎么记录上一次的答案,能从上一次 \(O(1)\) 转移。因为有 \(dis\),我们就记录 \(f_{i-1,s}-pos_s\) ,因为答案是 \(f_{i-1,s} + pos_j -pos_s\),与 \(s\) 有关的正是 \(f_{i-1,s} - pos_s\)。同理,我们记录 \(f_{i-1,s}+pos_s\) 便可以在 \(s\) 在 \(j\) 右侧的情况中用到。
当然还有 \(s = j\) 时。
那么我们原来要考虑整个关键点的转移,现在只要考虑三种类型的转移就行了,把一个 \(n\) 砍成了常数 \(3\)。
注意转移的意义,从前面转移求的是前缀最小;从后面转移求的是后缀最小。我调的时候求了个全局最小……唐完了。
接下来就可以吃上 \(O(n^2)\) 的 \(50\) 分了
const int N = 1e6+10;
int f[3][N];
int L[N],R[N];
int table[N];
int cnt{};
map<int,int>vis;
inline int aabs(int a)
{
return a >= 0 ? a : -a;
}
int cost[3][N];
int now{};
void work()
{
cost[1][cnt+1] = cost[0][0] = LONG_LONG_MAX;
for(int j{1};j<=cnt;j++) cost[0][j] = min(cost[0][j-1],f[now][j] - table[j]);
for(int j{cnt};j>=1;j--) cost[1][j] = min(cost[1][j+1],f[now][j] + table[j]);
}
signed main()
{
#ifdef LOCAL
freopen("in.in","r",stdin);
#endif
int n = read(),x = read();
vector<int>temp;
temp.push_back(x);
for(int i{1};i<=n;i++)
L[i] = read(),R[i] = read(),temp.push_back(L[i]),temp.push_back(R[i]);
sort(temp.begin(),temp.end());
int l = unique(temp.begin(),temp.end())-temp.begin();
for(int i{1};i<=l;i++) table[++cnt] = temp.at(i-1),vis[temp.at(i-1)] = cnt;
for(int i{1};i<=n;i++)
L[i] = vis[L[i]],R[i] = vis[R[i]];
memset(f,0x3f3f3f3f,sizeof(f));
f[0][vis[x]] = 0;
work();
now = 1;
for(int i{1};i<=n;i++)
{
for(int j{1};j<=cnt;j++) f[now][j] = LONG_LONG_MAX;
for(int j{1};j<=cnt;j++)
{
if(j >= L[i] && j <= R[i])
f[now][j] = min(f[now][j],f[now^1][j]),
f[now][j] = min(f[now][j],cost[1][j]-table[j]),
f[now][j] = min(f[now][j],cost[0][j]+table[j]);
else
f[now][j] = min(f[now][j],f[now^1][j]+min(aabs(table[L[i]]-table[j]),aabs(table[R[i]]-table[j]))),
f[now][j] = min(f[now][j],cost[1][j]-table[j]+min(aabs(table[L[i]]-table[j]),aabs(table[R[i]]-table[j]))),
f[now][j] = min(f[now][j],cost[0][j]+table[j]+min(aabs(table[L[i]]-table[j]),aabs(table[R[i]]-table[j])));
}
work();
now ^= 1;
}
now ^= 1;
int res = LONG_LONG_MAX;
for(int i{1};i<=cnt;i++) res = min(res,f[now][i]);
writeln(res);
return 0;
}
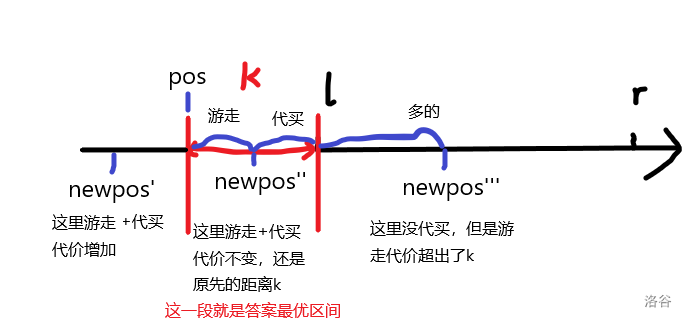
对于正解,先放张图。可以发现最优答案是一段区间,且在靠中部的位置,并不是一个单独的点。输出一些样例的 \(f_{n,j}\) 也可以发现这一点:如下图最后一行的答案 \(8\) 在中部且为一段区间。

所以我们要维护的是区间相等的位置以及他们的值。
开始时记 \(l = r = x,ans = 0\)。若下一个 \(L_i,R_i\) 包含它,不必修改;若包含了一部分,则不在 \(L_i,R_i\)内的点要增加答案,便不优,去掉这部分;若没有包含部分且 \(L_i > r\),那么所有值都要向右走,想想谁最优?越靠近 \(L_i\) 越优。所以 \([r,L_i]\) 为最优答案,\(ans + L_i-r\)。\(l>R_i\) 同理,越靠近 \(R_i\) 走的越少,\([R_i,l]\) 为最优,答案 \(ans - R_i + l\)。然后就做完了。
做到最后原来是个贪心……
int ll{x},rr{x};
int res{};
for(int i{1};i<=n;i++)
{
if(ll<=R[i] && L[i] <= rr) ll = max(ll,L[i]),rr = min(rr,R[i]);
if (R[i] < ll) {
res += ll - R[i];
rr = ll, ll = R[i];
}
if (L[i] > rr) {
res += L[i] - rr;
ll = rr, rr = L[i];
}
}
writeln(res);
T3 环上合并
给一个环,环长为 \(n\),每次操作可以把 \(a_i\) 换成 \(a_{i-1},a_i,a_{i+1}\) 中最大值或最小值,对于每个 \(k(1\le k \le m)\) 求出,最少操作多少次能使所有数都等于 \(k\)
T4 送快递
有 \(n\) 个点,其中每个点的位置为 \(a_i\)(不保证 \(a_i\) 单调递增啊),现在有 \(\text{wymx}\) 和 \(\text{wmw}\) 从初始点往 \(a_i\) 跳,跳到之后就要留在那个点,每一个点都要有人跳,求两人的最短跳跃路程和。
首先注意到有 \(n \le 20\) 的 \(20\) 分,又想到这个题天然符合状压的 \(0-1\) 状态,直接状压,一遍过样例(忽略初始极大值赋小)。
接下来 \(n \le 1000\),有 \(50 \text{pts}\),给 \(O(n^2)\) 的 \(\text{dp}\),但是状态不是很好设,所以我考场上甚至没有想到 \(\text{dp}\)。设 \(f_{i,j}\) 表示一个人到了 \(a_j\) 这个点,且另一个人在 \(a_i\) 这个点的最小总路程。
假设 \(\text{wmw}\) 到了 \(i-1\),下一个点如果 \(\text{wymx}\) 走,那么状态就将是 \(f_{i,i-1}\),而 \(\text{wymx}\) 可以从 \(i-1\) 后面的所有点走,即:\(f_{i,i-1}=\min\limits_{j=0}^{i-1} f_{j,i-1}+|a_i-a_j|\\\)。而如果 \(\text{wymx}\) 此时再向前进一步,就有 \(f_{i,j}=f_{i-1,j}+|a_i-a_{i-1}|\)。


