2024.8.13

T1 那一天我们许下约定

题意：求构造长度为 \(D\) 的元素总和为 \(N\) 且元素最大值小于 \(M\) 的序列方案。\(N,M\le 2000,D \le 10^{12}\)

30分

乱搞都是这个分，包括正解 \(\text{dp}\) 没优化也是。

说下我咋想的。往序列中填数，先不考虑 \(0\)，因为 \(0\) 的放法可以在放完其他元素之后组合算方案。那么相当于要求一个用正整数填 \(N\) 的方案。注意到最大值不超过 \(M\)，所以元素种类也就是 \(2000\) 了。那么就可以搜索剪枝，就搜每一种元素放了多少个，判断总和与已放序列长度，放好用组合数学算一下就行了。用当前序列长度的阶乘，把每个元素个数的阶乘都除掉，就是当前序列的排列了，再把 \(0\) 放在里面排列一下，就可以得到当前序列的答案了，求个和。

发现复杂度瓶颈是爆搜。也就是说只需要在正确复杂度内求出每种元素放多少个能凑出 \(n\)。考场上想了想 \(\text{dp}\) 不太会，再换思路也来不及了。

100 分

不考虑 \(0\)，只考虑非 \(0\) 元素，设 \(f_{i,j}\) 表示用 \(i\) 个位置总和放了 \(j\) 的方案。怎么想到？\(n,m\) 很小，所以可以通过位置和总和来列式子。想到这个状态这题就差不多结束了，因为转移是显然的：

\[\left\{\begin{matrix} f_{i,j} \Leftarrow f_{i,j}+\displaystyle \sum_{k=1}^{\min(m,j)}f_{i-1,j-k} \\ ans = \displaystyle\sum_{i=1}^{\min(n,d)}f_{i,n} \cdot C_{D}^{i} \end{matrix}\right. \]

然后发现是 \(O(n^3)\) 的，前缀和优化到 \(O(n^2)\)。然后就是 \(C_{D}^{i}\)，因为 \(D\) 最大是 \(10^{12}\)，所以肯定不能硬搞。手模出递推式：\(C_{D}^{i} = C_{D}^{i-1}\frac{D-i+1}{i}\)，然后 \(O(n)\) 转移预处理，注意这里在算的时候随便一乘就是一个 \(10^{12}\)，取模应当非常充分，然后注意到内存就只有可怜的 \(64 MiB\)，因此我们还不敢轻易 #define int __int128，因此我们可以使用 C[i] = ((__int128)C[i-1]*(d-i+1)) % MOD;

T2 那一天她离我而去

题意：求无向图以 \(1\) 为起点的最小环，\(n \le 1 \times 10^4\)，\(m \le 4 \times 10^4\)。

暴力做法：注意到环一定是从一条连 \(1\) 的边出去，再从另一个连 \(1\) 的边进来。那么不妨分别断掉每一条 \(1\) 所连的边，以其连节点跑到 \(1\) 的最短路，再加上这条边的权，求最小值，理论复杂度 \(O(cnt\cdot n)\)，显然给个菊花就死了。

以下图为例，我们便可以删掉一个 \(1 \rightarrow2\) 的边，从 \(2\) 向 \(1\) 跑最短路，加上 \(w_{1\rightarrow2}\) 便得到了这个环长。

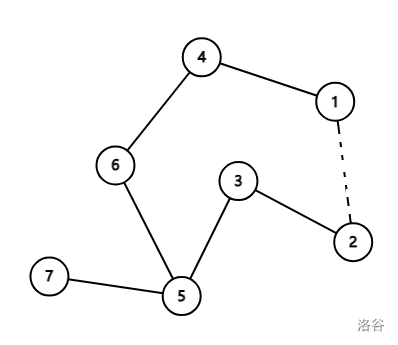
现在的复杂度 \(O(cnt\cdot n)\)，是可以被卡到 \(O(n^2)\) 的，考虑优化。就拿上图举例子，我们把最小环拿出来，这个环一定与 \(1\) 有两个连边，枚举环的过程就是在枚举与 \(1\) 相连的两两节点。这样枚举的复杂度是 \(O(cnt^2)\) 的，更垃圾。

但是我们发现，枚举这两个节点时，我们并不关心其他节点，因为最小环必然不会经过其他与 \(1\) 相连的节点，因此保证正确性。我们便可以对这些与 \(1\) 连接的点进行分组，把一个组与 \(1\) 的连边删掉，并连接到源点 \(n+1\)（权值与到 \(1\) 的相同），从 \(1\) 跑到 \(n+1\)，最短路就是这两组之间的最小环了。因此只要把答案点分开到两个不同的组就能出解了。怎样保证把答案点分到两组呢？考虑到它俩编号必然不一样，所以按二进制每一位的 \(0,1\)，必然在某几次能分到不同的组去，那就可以做到 \(O(n \log cnt)\) 了。

T3 哪一天她能重回我身边

本场 \(\text{MVP}\)。

她依然在我不知道的地方做我不知道的事。
桌面上摊开着一些卡牌，这是她平时很爱玩的一个游戏。如今卡牌还在，她却不在我身边。不知不觉，我翻开了卡牌，回忆起了当时一起玩卡牌的那段时间。
每张卡牌的正面与反面都各有一个数字，我每次把卡牌按照我想的放到桌子上，而她则是将其中的一些卡牌翻转，最后使得桌面上所有朝上的数字都各不相同。
我望着自己不知不觉翻开的卡牌，突然想起了之前她曾不止一次的让我帮她计算最少达成目标所需要的最少的翻转次数，以及最少翻转达成目标的方案数。
（两种方式被认为是相同的当且仅当两种方式需要翻转的卡牌的集合相同）
如果我把求解过程写成程序发给她，她以后玩这个游戏的时候会不会更顺心一些？

暴力：状压枚举每个牌翻或不翻，\(O(n) \text{check}\) 一下，算方案。

正解：懒得写了

T4 战争调度

满二叉树，每个节点权值为 \(0\) 或 \(1\)，状态自定。叶子节点对答案有贡献当且仅当它的 \(k\) 级祖先跟他权值相同，若都为 \(1\)，有 \(w_{i,k}\) 的贡献；若都为 \(0\)，有 \(f_{i,k}\) 的贡献。叶子节点 \(1\) 的个数不能超过 \(m\)。求树的最大贡献值。

深度 \(n \in [2,10]\),\(m\le2^{n-1}\)。

这题样例给了跟给了一样，我输入把 \(f,w\) 顺序反了都能出。

状压枚举每个节点的状态复杂度是 \(O(2^{2^{n}-1})\)，可以过掉 \(20\) 分。既然我们可以枚举祖先状态，通过祖先状态来算出当前贡献，我们就可以 \(\text{dp}\) 了。注意到限制条件在叶子节点的打仗人数，不妨将叶子节点的打仗人数纳入状态。设 \(f_{u,i}\) 表示节点编号为 \(u\) ，子树中叶子节点中有 \(i\) 个人打仗的最大贡献，便有 \(f_{u,i+j} \Leftarrow \max(f_{u,i+j},f_{u<<1,i} + f_{u<<1|1,j})\)，即从左右子树汇总答案。

然后只需要 \(\text{dfs}\) 往下推的时候推两次不同的当前状态，推到叶子节点计算总答案，复杂度可类比线段树，为 \(O(2^{n-1}\log 2^{n-1})\)。再往上传，每次按照上式 \(O(m^2)\) 算一下值，不断上推到根节点，在根上取最大值就完了。

#define lson(x) x<<1
#define rson(x) x<<1|1
void dfs(int x,int s,int siz)
{
    for(int i{};i<=siz;i++) f[x][i] = 0;
    if(siz == 1)
    {
        for(int i{1};i<=n-1;i++)
            if((s >> (i-1)) & 1) f[x][1] += val1[x][i];
            else f[x][0] += val0[x][i];
        return;
    }
    for(int now{};now<=1;now++)
    {
        dfs(lson(x),s<<1|now,siz>>1),dfs(rson(x),s<<1|now,siz>>1);
        for(int i{};i <= min(siz,m);i++)
        for(int j{};i+j <= min(siz,m);j++)
            f[x][i+j] = max(f[x][i+j],f[lson(x)][i]+f[rson(x)][j]);
    }
}

signed main()
{
	#ifdef LOCAL
	freopen("in.in","r",stdin);
	#endif
 	n = read(),m = read();
    for(int i{qp(2,n-1)};i < qp(2,n);i++)
        for(int j{1};j < n;j++) val1[i][j] = read();
    for(int i{qp(2,n-1)};i < qp(2,n);i++)
        for(int j{1};j < n;j++) val0[i][j] = read();
    dfs(1,0,qp(2,n)-1);
    for(int i{};i<=m;i++)
        ans = max(f[1][i],ans);
    writeln(ans);
    return 0;
}