2024.8.19
最高的一次
\(100+80+49+30,\text{rk1}\)。
T1 电压
给一个无向有环图,每个点的权值在 \(0,1\) 中自定,问存在多少条边可以构造出方案,使这条边的两端权值相同,其余所有边两端权值不同。图不一定联通,有重边。
- 首先可以想到没有环的情况。手搓几个图可以发现,任意一条边都可以作为答案边,那么答案就是 \(m\)。
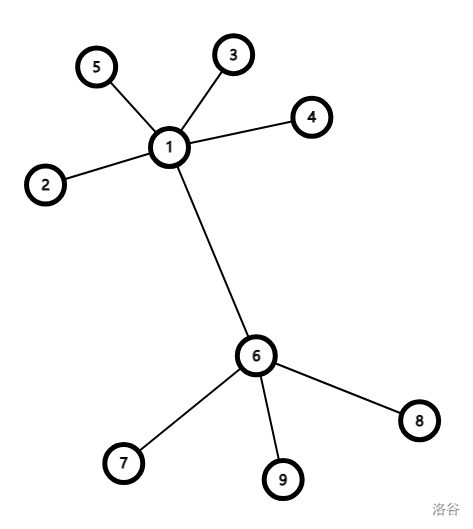
在没有环的情况下,对于每一个联通子图来说,都是一棵树。断掉树上的一条边作为答案边,便会把树分裂成两棵子树。在这两棵子树中,会分别形成 “父子之间权值不同” 这样的限制关系。这样的限制关系使我们联想到 \(7.25\) 的 \(\text{T3}\):\(\text{ball collector}\),结论是树的所有边都可以满足,那么这条边就是可断的。既然每条树边都可断,那么总答案就是边数了。
- 在有环的情况下,发现答案边只能在所有奇环的交汇处,并且不在任意一个偶环中。
手搓几个图可以发现,满足一边两点权值相同的限制关系并且要让环上其他边均满足权值不同,必须使该环的边数为奇数。因此一个边数为偶数的环中,是不可能出现答案边的。答案边在奇环上,因为只要让奇环中的其他边都满足两端权值不同,就会存在一条两端权值相同的边。且这样的边一次构造只能存在一条,因此要让答案边位于所有奇环上,即奇环的交汇处。
接下来就是判断环并且统计奇环个数了。注意我们并不关心偶环个数,因为我们判断边的标准是所有奇环的交汇并且经过偶环数为 \(0\),因此我们只需要判断当前边所在奇环的个数是不是总奇环个数就可以。我们 \(\text{dfs}\) 跑每一个联通块,当出现返祖边是便找到了环,这时会出现一个时间戳的差值,我们恰好可以用 “深度” 来实现。手搓一下,如果原深度和返祖深度之差为偶数,那么出现了一个奇环;否则出现了偶环。接下来用差分,我们将边权下放到点,便可以在不断回溯的过程中将这个环找出来。注意有一个细节,环初边的下放是没有统计上的,这里在后面特判。
接下来就是计算答案了,我们遍历每个点,看看这个点所对应的边是不是在所有奇环中,并且不在偶环中。这里有两个特判(面向样例):
- 计算点不能是每个联通块的根。(会在第二个样例中发现)我们点的意义是边权下放,根是没有意义的。可能会出现恰好数值相同的情况,就会多算。
- 当奇环只有一个时,答案要 \(+1\)。(会在第三个样例中发现)记得我们刚才少算了一条边。因为只有一个奇环的时候,环上所有边都要计入答案,这时便会少算。而至少有两个奇环时,手玩发现不会少算。
T2 农民
对于操作3,一个点的所有祖先都会对其有一个限制,所以我们只需要判断当前点到根的路径上的限制是否都能满足即可。考虑用树剖+线段树维护这个限制。
对于翻转操作,我们需要维护当前区间左儿子限制最小值/最大值 和 右儿子最小值 / 最大值。
还要注意翻转操作会导致树的形态改变。
T3 奇迹树
构造题我们可以从样例入手。这里使用第二个样例:
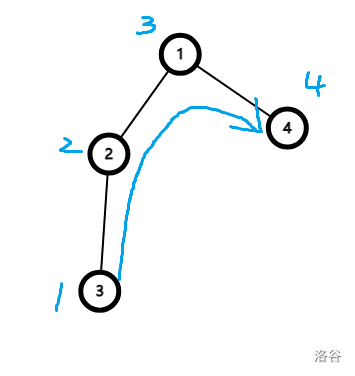
我们发现填数的顺序是从一个子树的底部向根,再填向下一个子树。考虑到形式过于单一,我们将图进行扩展。
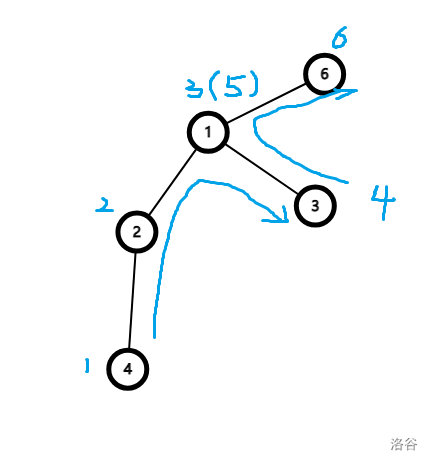
如果给 \(1\) 添加一个父节点,那么再向上填的时候,可以手搓出来,新点应该填上 \(6\)。因为要在与 \(3\) 节点的限制关系中满足和它的点权差为 \(2\) ,要递增还要取最小。接下来思考它究竟是怎么填上的,其实是我们从 \(3\) 跳到父亲 \(1\) 节点后再向上跳,这个过程不断累计计数器使得 \(6\) 节点处填 \(6\)。这时我们发现 \(1\) 节点处既可以填原有的 \(3\) 也可以覆盖上新序 \(5\),因为我们构造的限制条件在最大值最小,和点权差不小于两点距离。在满足最大值不变时,其他点只需要满足要求即可。
这时我们便得到了一种构造方法,但我们的过程是从下往上,不容易实现。便可以从上往下,按照 \(\text{dfs}\) 的顺序填编号(因为保证了两两差的绝对值不变,且最大最小值不变)。我们惊喜地发现,这就是欧拉序。
而我们从上往下遍历的过程中,必然会回溯。回溯的过程中是需要不断累计计数器的。那么需要让最终累计到的值最小,必然要保证回溯的过程越短越好。这时就需要保证直径不能回溯,当且仅当不回溯直径,点权最大值取到最小。那么我们就找到树的直径,从直径的一个端点开始 \(\text{dfs}\),遍历子树的过程中,将在直径中的点拉出来,每次遍历的时候最后遍历就好了。
T4 相逢是问候
\(c^{c^{c^{\cdots}}}\bmod p\)可以转化为\(c^{c^{c^{\cdots}\bmod \varphi(p)+\varphi(p)}}\bmod p\),反复嵌套即可算出。
又注意到,在指数的层数达到一定值后就不再变化,可以考虑维护其单点修改次数,修改时直接暴力,达到临界后就不再更改。
于是考虑线段树维护一个区间的最小修改次数。
然后是最后的优化。欧拉函数很少,意味着模数很少,考虑将快速幂预处理,分为\(c^i\bmod p\)与\(c^{10000\times i}\bmod p\),查询时直接将两块进行拼接。


