牛课网--走格子（环形遍历数组并且找出指定步数的位置）

题目链接：https://www.nowcoder.com/acm/contest/114/A

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int A[105],cnt;
void span(int x)
{
    cnt = 1;
    A[cnt++] = 0;
    if(x == 1) return ;
    if(x == 2)
    {
        A[cnt++] = 3;
        return ;
    }
    int sum = 0,cn = 1;
    while(1)
    {
        if(x - cn == 1)
        {
            sum = sum + 3;
            A[cnt++] = sum;
            break;
        }
        if(x - cn == 0)
        {
            break;
        }
        sum = sum + (x-cn)*4;
        A[cnt++] = sum;
        cn = cn + 2;
    }
    return ;
}
void path(int po,int cha,int n)
{
    int l=1+po-1;
    int r=n-po+1;
    int x=po,y=po;
    int op=1;
    while(cha)
    {
        if(op==1)
        {
            if(x+1==r) op++;
            x++;
        }
        else if(op==2)
        {
            if(y+1==r) op++;
            y++;
        }
        else if(op==3)
        {
            if(x-1==l) op++;
            x--;
        }
        else
        {
            y--;
        }
        cha--;
    }
    printf("%d %d\n",x,y);
}
int main()
{
    int n,m;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        memset(A,0,sizeof(A));
        span(n);
        int l,r,cha,vis=0;
        for(int i=1;i<cnt;i++) //m
        {
            if(m == A[i]) {vis=i;break;}
            if(m>A[i]) l=i;
            if(m<A[i]) {r=i;break;}
        }
        cha=m-A[l];
        if(vis!=0)
        {
            printf("%d %d\n",vis,vis);
        }
        else path(l,cha,n);
    }
    return 0;
}

分析：

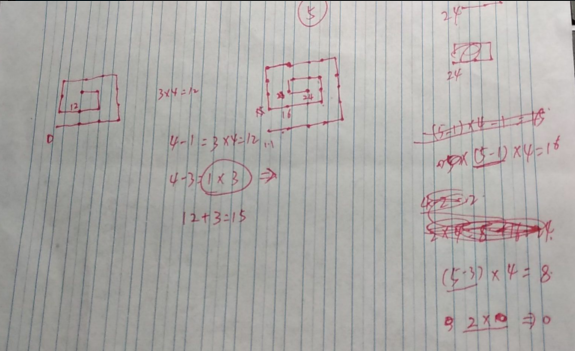
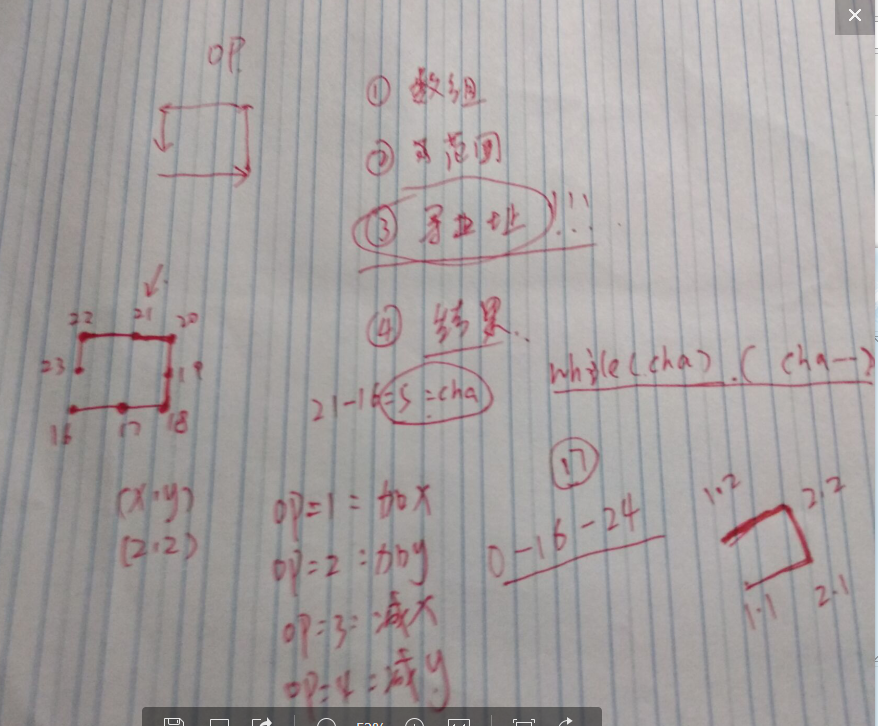
这道题目不用数组做，只要善于发现一些小规律就好了，做出这道题目最大的原因就是冷静分析，拆分题目！

题目拆分主要为3部分：

1.如图一，对于给出的每一个边长，我们用数组储存每一圈对应可以走多少步。需要注意的是，偶数边与奇数的边对应的圈数不同。

2.对于第二个参数m，我们定位到它位于数组的哪一个范围之间，然后在对应的那一圈里面寻找就好了。（特殊：要考虑到m的步数值刚好落在每一层开始的点）

3，也是最重要的一步，就是根据所在的圈数，算出差值还差多少步，初始化x,y坐标为层数刚开始的点的坐标，遍历到这一层对应差值的点，这里遍历一圈无非是4种不同的

坐标记录方法，可以用op代表正在执行的操作种类，最后x,y对应的值就是解。

 

总结：这道题应该是大比赛上的签到题，它属于那种要心细还要冷静分析才能解决的题目，涉及到题目的分析，这一点非常的关键！！不要一上来就是二维数组的环形遍历，要找规律，找突破点，拆分题目！！最后，请带着你最初的梦想继续前进吧！

2018,6,9,1:35

 

---------------------------------------------------------分割线---------------------------------------------------------

也许是我们都把问题想的太过于复杂了，但是根本的原因还是接触的题型不够多。比赛完了之后，看了一下段诩大佬的代码，简短有力，思路明确，这就是区别，见贤思齐，以后多多参悟段诩的代码，提高自身水平。#include <bits/stdc++.h> //知识点1using namespace std;

 
typedef long long ll;
 
const int kMax = 1010;
 
const int dx[] = {1, 0, -1, 0};    //这是整道他解题的关键，利用方向数组来实现朝着指定方向遍历，也就是所谓的环形遍历
const int dy[] = {0, -1, 0, 1};
 
int n, m;
bool vis[kMax][kMax];               //这个数组就是记录下有没有被遍历过
 
void solve(int x, int y) {
    int d = 0;
    memset(vis, false, sizeof(vis));
    vis[x][y] = true;
    while (m--) {
        for (int i = 0; i < 4; ++i) {
            d = (d + i) % 4;         //这里要对4取余，是因为4次之后，d=4的方向与d=0一样，所以取余
            int tx = x + dx[d], ty = y + dy[d];
            if (tx >= 0 && tx < n && ty >= 0 && ty < n && !vis[tx][ty]) {    //这个选择条件亦是很重要，遍历的时候，保证坐标不能越界，不能重复遍历
                x = tx;
                y = ty;
                break;           //这里添加break，是因为坐标满足了一个方向遍历的条件，break出去之后，还是朝着原来的方向继续走。
            }                                                    //当坐标遇到需要拐弯时，进不来这个if,那么d就会根据i来改变方向。
        } 
        vis[x][y] = true; 
    } 
    printf("%d %d\n", x + 1, y + 1); 
}
int main()
{ 
    scanf("%d%d", &n, &m);
    solve(0, 0); 
    return 0;
}

这道题目需要学到的：

1.d方向值+break巧妙使用，以前都是直接for四个方向，然后就直接根据i来选择方向了，但是在这道题目中，d才是真正决定走哪个方向的值，还有当我满足那个if选择条件的时候，我就break掉了，那么不管d的值如何，那么下一次进来的时候，d还是保持原来的值，那么我的方向就不会改变，除非你不在能够满足我的if条件，那么我才会改变d的下一个方向的值。

2.对4取余，是因为d=0与d=4的走的方向一样，所以对4取余，保证了当d=4的时候，重新开始计数d

3.#include<bits/stdc++.h> 这个头文件几乎包含了C++所有的头文件库，相当于引入了所有的标准函式库！！以后就不用再打长长的一串头文件了。