【ZJOI2017 Round2练习&BZOJ4827】D1T3 gift（FFT）

题意：

 

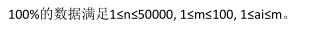
思路：可以看出题目所要最小化的是这样一个形式：

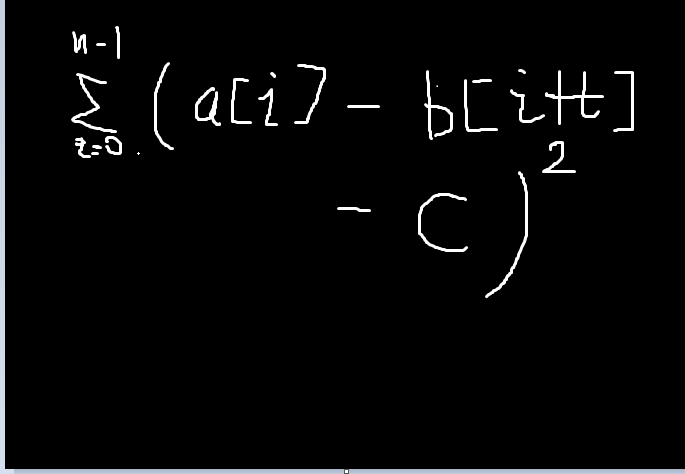
拆出每一项之后发现会变化的项只有sigma a[i]*b[i+t]与c^2,c*(a[i]-b[i])

c可以在外层枚举，剩下的只有sigma a[i]*b[i+t] (i=0..n-1)

因为FFT只能解决simga a[i]*b[n-i]

所以我们可以把a翻转，这样就化成了如上的形式

c[n+t+1]=a[n-i+1]*b[i+t] (i=0..n-1)

取出最小（大）的c[i]，与外层枚举的c共同求出答案，取最小值

FFT模板，值得一背

  1 type cp=record
  2          x,y:extended;
  3         end;
  4      arr=array[0..510000]of cp;
  5 var c,d,cur:arr;
  6     a,b:array[0..510000]of longint;
  7     n,i,m:longint;
  8     ans,sum,s1,s2:int64;
  9 
 10 procedure swap(var x,y:cp);
 11 var t:cp;
 12 begin
 13  t:=x; x:=y; y:=t;
 14 end;
 15 
 16 function jia(a,b:cp;f:longint):cp;
 17 begin
 18  if f=-1 then
 19  begin
 20   b.x:=-b.x; b.y:=-b.y;
 21  end;
 22  jia.x:=a.x+b.x;
 23  jia.y:=a.y+b.y;
 24 end;
 25 
 26 function mult(a,b:cp):cp;
 27 begin
 28  mult.x:=a.x*b.x-a.y*b.y;
 29  mult.y:=a.x*b.y+a.y*b.x;
 30 end;
 31 
 32 function min(x,y:int64):int64;
 33 begin
 34  if x<y then exit(x);
 35  exit(y);
 36 end;
 37 
 38 function max(x,y:int64):int64;
 39 begin
 40  if x>y then exit(x);
 41  exit(y);
 42 end;
 43 
 44 procedure fft(var a:arr;n,f:longint);
 45 var i,j,k,m:longint;
 46     w,u,v:cp;
 47 begin
 48  i:=n>>1; j:=1;
 49  while j<n do
 50  begin
 51   if i<j then swap(a[i],a[j]);
 52   k:=n>>1;
 53   while k and i>0 do
 54   begin
 55    i:=i xor k;
 56    k:=k>>1;
 57   end;
 58   i:=i xor k;
 59   inc(j);
 60  end;
 61  m:=2;
 62  while m<=n do
 63  begin
 64   w.x:=cos(2*pi*f/m); w.y:=sin(2*pi*f/m);
 65   cur[0].x:=1; cur[0].y:=0;
 66   for i:=1 to m-1 do cur[i]:=mult(cur[i-1],w);
 67   i:=0;
 68   while i<n do
 69   begin
 70    j:=i;
 71    while j<i+(m>>1) do
 72    begin
 73     u:=a[j]; v:=mult(a[j+(m>>1)],cur[j-i]);
 74     a[j]:=jia(u,v,1);
 75     a[j+(m>>1)]:=jia(u,v,-1);
 76     inc(j);
 77    end;
 78    i:=i+m;
 79   end;
 80   m:=m<<1;
 81  end;
 82 end;
 83 
 84 procedure solve;
 85 var i,j,len:longint;
 86 begin
 87  for i:=0 to n-1 do c[i].x:=a[i];
 88  for i:=0 to n-1 do d[i].x:=b[i];
 89  i:=0; j:=n-1;
 90  while i<=j do
 91  begin
 92   swap(d[i],d[j]);
 93   inc(i); dec(j);
 94  end;
 95  len:=1;
 96  while len<=n+n do len:=len<<1;
 97  for i:=n to len-1 do
 98  begin
 99   c[i].x:=0; d[i].x:=0;
100  end;
101  for i:=0 to len-1 do
102  begin
103   c[i].y:=0; d[i].y:=0;
104  end;
105  fft(c,len,1);
106  fft(d,len,1);
107  for i:=0 to len-1 do c[i]:=mult(c[i],d[i]);
108  fft(c,len,-1);
109  for i:=0 to len-1 do c[i].x:=trunc(c[i].x/len+0.5);
110  for i:=n to len-1 do c[i mod n].x:=c[i mod n].x+c[i].x;
111  sum:=-(1<<62);
112  for i:=0 to n-1 do sum:=max(sum,round(c[i].x));
113  sum:=-sum*2;
114 end;
115 
116 begin
117  assign(input,'bzoj4827.in'); reset(input);
118  assign(output,'bzoj4827.out'); rewrite(output);
119  readln(n,m);
120  for i:=0 to n-1 do read(a[i]);
121  for i:=0 to n-1 do read(b[i]);
122  ans:=1<<62;
123  solve;
124  for i:=0 to n-1 do
125  begin
126   s1:=s1+a[i]-b[i];
127   s2:=s2+a[i]*a[i]+b[i]*b[i];
128  end;
129  for i:=-m to m do ans:=min(ans,int64(n)*i*i+2*s1*i+s2+sum);
130  writeln(ans);
131  close(input);
132  close(output);
133 end.

 

posted on 2017-04-19 20:46  myx12345  阅读(212)  评论(0)  编辑  收藏  举报

导航