【BZOJ2301】Problem b（莫比乌斯反演）

题意：对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，

且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

思路：第一题反演……

利用容斥原理将原询问拆成4个，问题就转化为：

1<=i<=trunc(a div k)，1<=j<=trunc(b div k)，gcd(i,j)=1的(i,j)数对个数

令f(i)表示满足gcd(x,y)=i时(x,y)的对数，F(i)表示满足i|gcd(x,y)的(x,y)的对数

显然F(i)=trunc(n div i)*trunc(m div i)

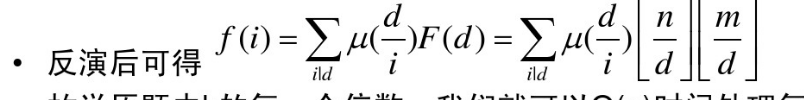
f(1)=sigma u(d)*n div d*m div d (1<=d<=n)

观察可得n div d*m div d只有2根号n个取值，且每个取值对应的u(i)是连续的一段

然后就可以记录u的前缀和来优化

From  http://m.blog.csdn.net/article/details?id=50590197

 1 //uses sysutils;
 2 const max=50000;
 3 var mu,sum,prime:array[0..max]of longint;
 4     flag:array[0..max]of longint;
 5     a,b,c,d,k,i,j,t,m,cas,v:longint;
 6     tmp:double;
 7 
 8 procedure swap(var x,y:longint);
 9 var t:int64;
10 begin
11  t:=x; x:=y; y:=t;
12 end;
13 
14 function clac(n,m:longint):int64;
15 var i,t1,t2,pos:longint;
16     x,y:int64;
17 begin
18  if n>m then swap(n,m);
19  clac:=0; i:=1;
20  while i<=n do
21  begin
22   x:=n div i; y:=m div i;
23   t1:=n div x;
24   t2:=m div y;
25   if t1<t2 then pos:=t1
26    else pos:=t2;
27   clac:=clac+x*y*(sum[pos]-sum[i-1]);
28   i:=pos+1;
29  end;
30 end;
31 
32 begin
33  assign(input,'bzoj2301.in'); reset(input);
34  assign(output,'bzoj2301.out'); rewrite(output);
35 // tmp:=now;
36  read(cas);
37  mu[1]:=1;
38  for i:=2 to max do
39  begin
40   if flag[i]=0 then
41   begin
42    inc(m); prime[m]:=i;
43    mu[i]:=-1;
44   end;
45   j:=1;
46   while (j<=m)and(prime[j]*i<=max) do
47   begin
48    t:=prime[j]*i;
49    flag[t]:=1;
50    if i mod prime[j]=0 then
51    begin
52     mu[t]:=0;
53     break;
54    end;
55    mu[t]:=-mu[i];
56    inc(j);
57   end;
58  end;
59  for i:=1 to max do sum[i]:=sum[i-1]+mu[i];
60  for v:=1 to cas do
61  begin
62   read(a,b,c,d,k);
63   dec(a); dec(c);
64   a:=a div k; b:=b div k; c:=c div k; d:=d div k;
65   writeln(clac(b,d)-clac(b,c)-clac(a,d)+clac(a,c));
66  end;
67  //writeln((now-tmp)*86400:0:2);
68  close(input);
69  close(output);
70 end.

 UPD（2018.10.22）：C++

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<string>
 4 #include<cmath>
 5 #include<iostream>
 6 #include<algorithm>
 7 #include<map>
 8 #include<set>
 9 #include<queue>
10 #include<vector>
11 using namespace std;
12 typedef long long ll;
13 typedef unsigned int uint;
14 typedef unsigned long long ull;
15 typedef pair<int,int> PII;
16 typedef vector<int> VI;
17 #define fi first
18 #define se second
19 #define MP make_pair
20 #define N   51000
21 #define M   410000
22 #define eps 1e-8
23 #define pi  acos(-1)
24 #define oo  1e9
25  
26 int mu[N+10],s[N+10],prime[N+10],flag[N+10];
27   
28 ll calc(int n,int m)
29 {
30     if(n>m) swap(n,m);
31     ll ans=0; 
32     int i=1;
33     while(i<=n)
34     {
35         ll x=n/i;
36         ll y=m/i;
37         int t1=n/x;
38         int t2=m/y;
39         int pos=min(t1,t2);
40         ans+=x*y*(s[pos]-s[i-1]);
41         i=pos+1;
42     }
43     return ans;
44 }
45  
46 int main()
47 {
48     int cas;
49     scanf("%d",&cas);
50     mu[1]=1;
51     int m=0;
52     for(int i=2;i<=N;i++)
53     {
54         if(!flag[i])
55         {
56             prime[++m]=i;
57             mu[i]=-1;
58         }
59         for(int j=1;j<=m;j++)
60         {
61             int t=prime[j]*i;
62             if(t>N) break;
63             flag[t]=1;
64             if(i%prime[j]==0) 
65             {
66                 mu[t]=0;
67                 break;
68             }
69             mu[t]=-mu[i];
70         }
71     }
72     for(int i=1;i<=N;i++) s[i]=s[i-1]+mu[i];
73     while(cas--)
74     {
75         int a,b,c,d,k;
76         scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
77         a--; c--;
78         a/=k; b/=k; c/=k; d/=k;
79         ll ans=calc(b,d)-calc(b,c)-calc(a,d)+calc(a,c);
80         printf("%lld\n",ans);
81     }
82     return 0;
83 }

 

 

 

 

 

 

posted on 2017-04-04 20:56  myx12345  阅读(427)  评论(0)  编辑  收藏  举报

导航