【BZOJ1061】志愿者招募（单纯形，对偶性）

题意:

这个项目需要N 天才能完成，其中第i 天至少需要

Ai 个人。 布布通过了解得知，一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天，招募费用

是每人Ci 元。新官上任三把火，为了出色地完成自己的工作，布布希望用尽量少的费用招募足够的志愿者，但这

并不是他的特长！于是布布找到了你，希望你帮他设计一种最优的招募方案。

第一行包含两个整数N, M，表示完成项目的天数和可以招募的志愿者的种类。 接下来的一行中包含N 个非负

整数，表示每天至少需要的志愿者人数。 接下来的M 行中每行包含三个整数Si, Ti, Ci，含义如上文所述。为了

方便起见，我们可以认为每类志愿者的数量都是无限多的。

1 ≤ N ≤ 1000，1 ≤ M ≤ 10000，题目中其他所涉及的数据均 不超过2^31-1。

思路：线性规划的对偶性 参见《算导》29章

全幺模矩阵可以保证至少有一组整数解

就是a[i,j]取值只为-1,0,1的矩阵

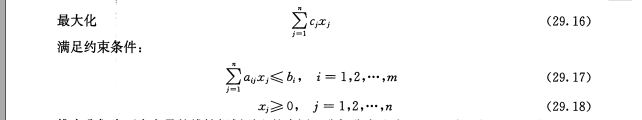
这个线性规划根据对偶性等价于

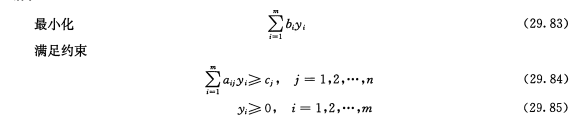
const eps=1e-8;
var a:array[0..10000,0..1000]of double;
    idx,idy,q:array[0..10000]of longint;
    b,c:array[0..10000]of double;
    n,m,i,j,op,x,y:longint;
    mn,p:double;

procedure swap(var x,y:longint);
var t:longint;
begin
 t:=x; x:=y; y:=t;
end;

procedure povit(x,y:longint);
var i,j,tot:longint;
    tmp:double;

begin
 swap(idx[y],idy[x]);
 tmp:=a[x,y]; a[x,y]:=1/a[x,y];
 for i:=0 to n do
  if y<>i then a[x,i]:=a[x,i]/tmp;
 tot:=0;
 for i:=0 to n do
  if (i<>y)and((a[x,i]>eps)or(a[x,i]<-eps)) then
  begin
   inc(tot); q[tot]:=i;
  end;
 for i:=0 to m do
 begin
  if (x=i)or((a[i,y]<eps)and(a[i,y]>-eps)) then continue;
  for j:=1 to tot do a[i,q[j]]:=a[i,q[j]]-a[x,q[j]]*a[i,y];
  a[i,y]:=-a[i,y]/tmp;
 end;
end;

function min(x,y:longint):longint;
begin
 if x<y then exit(x);
 exit(y);
end;

begin
 assign(input,'bzoj1061.in'); reset(input);
 assign(output,'bzoj1061.out'); rewrite(output);
 randomize;
 readln(n,m);
 for i:=1 to n do read(c[i]);
 for i:=1 to m do
 begin
  readln(x,y,b[i]);
  for j:=x to y do a[i,j]:=1;
 end;


 for i:=1 to n do a[0,i]:=c[i];
 for i:=1 to m do a[i,0]:=b[i];
 for i:=1 to n do idx[i]:=i;
 for i:=1 to m do idy[i]:=i+n;
 while true do
 begin
  x:=0; y:=0;
  for i:=1 to m do
   if (a[i,0]<-eps)and((x=0)or(random(2)=1)) then x:=i;
  if x=0 then break;
  for i:=1 to n do
   if (a[x,i]<-eps)and((y=0)or(random(2)=1)) then y:=i;
  if y=0 then break;
  povit(x,y);
 end;
 while true do
 begin
  x:=0; y:=0; mn:=1e15;
  for i:=1 to n do
   if a[0,i]>eps then begin y:=i; break; end;
  if y=0 then break;
  for i:=1 to m do
   if (a[i,y]>eps)and(a[i,0]/a[i,y]<mn) then
   begin
    mn:=a[i,0]/a[i,y]; x:=i;
   end;
  if x=0 then break;
  povit(x,y);
 end;
 writeln(-a[0,0]:0:0);
 close(input);
 close(output);
end.