【对称密码】DES加密算法
前言
本篇博文将介绍对称密码算法中的DES密码的算法原理与代码实现(Java)
DES算法原理
DES加密算法是对称加密算法(加密和解密使用同一个密钥)中的一种,DES也是分组密码,以64位为分组对明文进行加密。
DES算法会对明文进行16轮的迭代加密,具体的算法过程可以看下面这图(来自文末参考博文中的图,做了一些修改)。看一遍有点绕就那笔跟着走一遍。
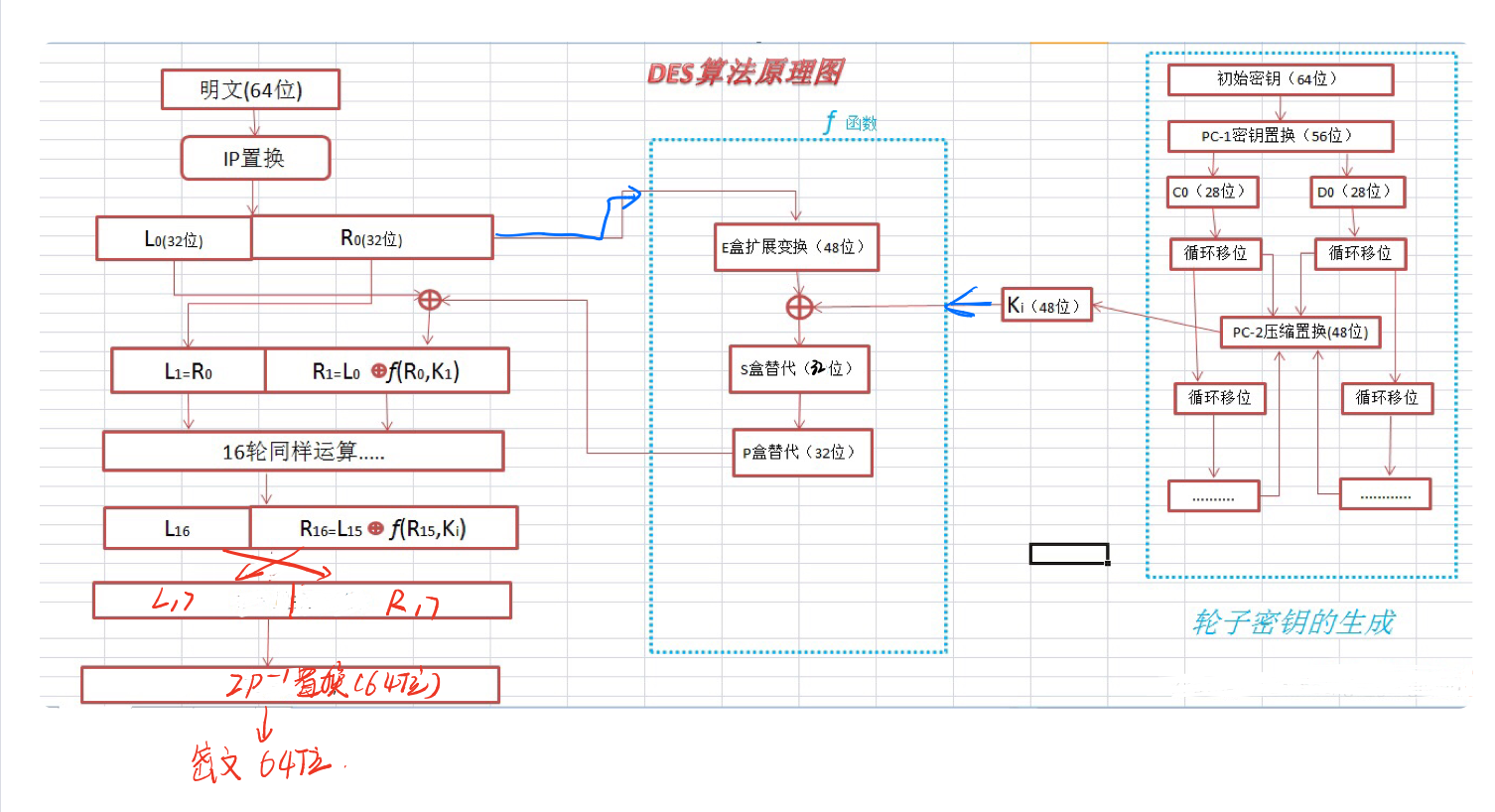
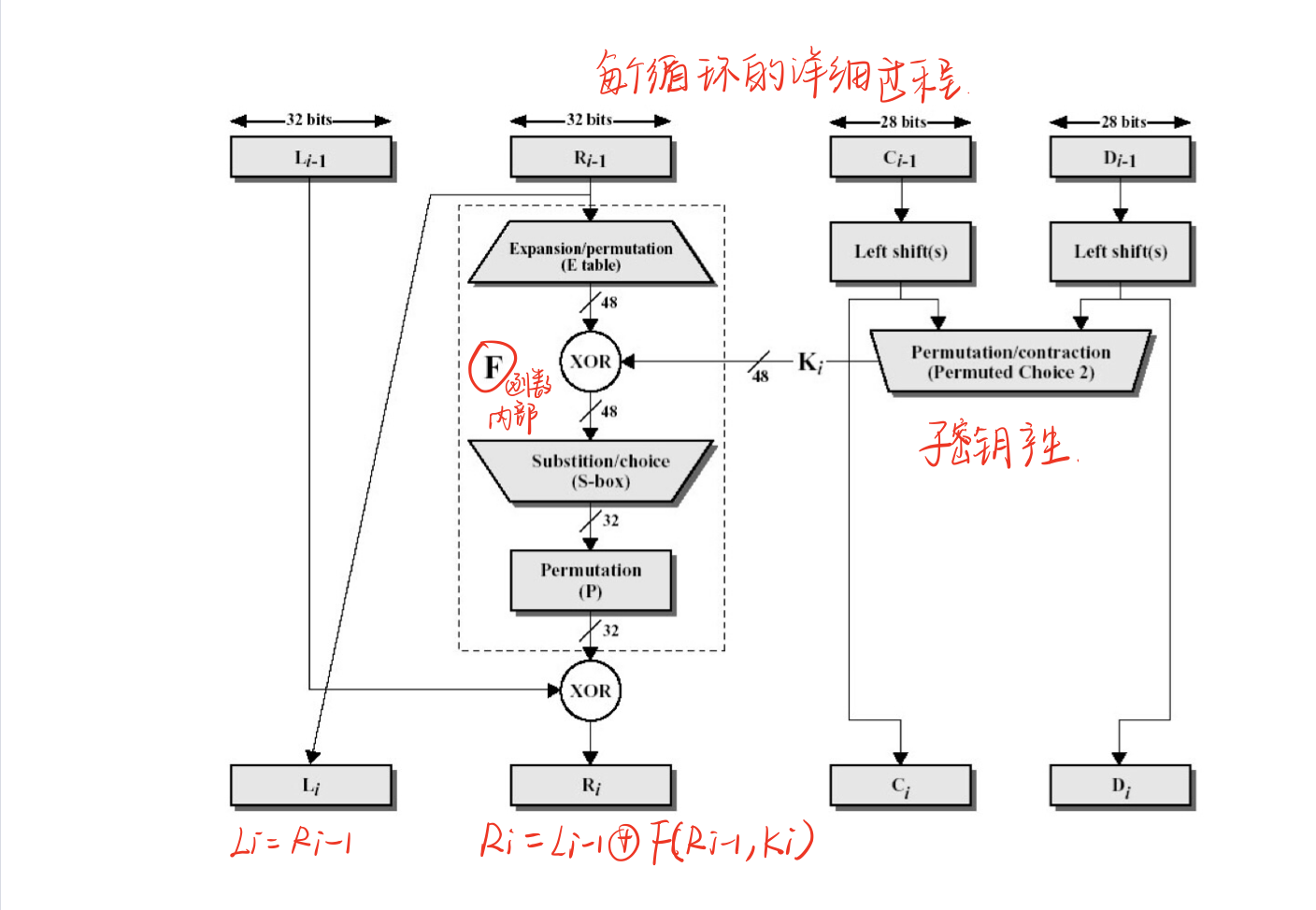
下面这张图是每次迭代的的一个提取,我们从中可以直接观察到的就是迭代的两个规律:
Li = Ri-1
Ri = Li-1 ^ F(Ri-1, Ki)
上一轮的输出作为下一轮加密的输入(也就是迭代的过程)。同样,子密钥也是迭代产生。
在总体概览了一遍后,我们可以将DES算法分为3部分来讲解。从第一张图从右往左,轮子密钥(子密钥)的生成、F函数的实现以及16次迭代的过程。
子密钥的产生
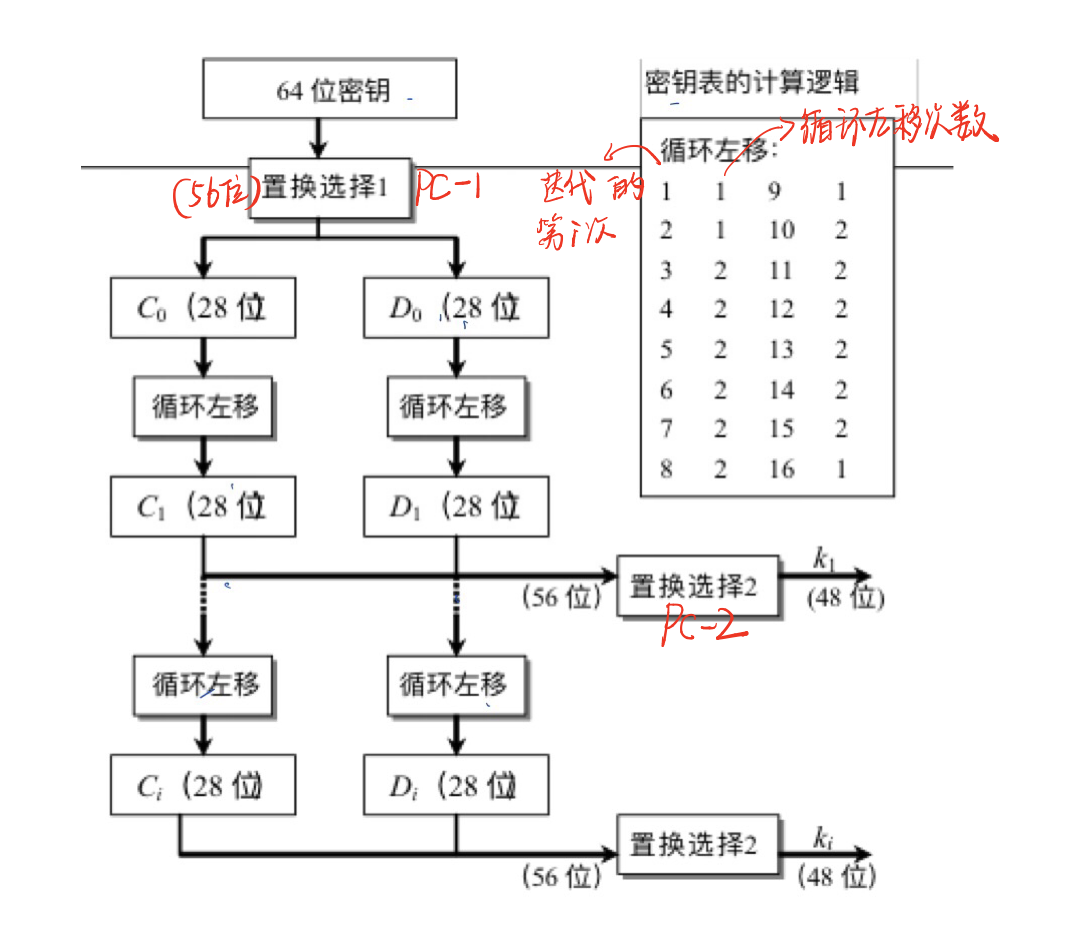
如图上的流程图所示,将所给的初始64位密钥(若是密钥不足64位则前面加0补充至64位),经过PC-1置换压缩成56位。然后分成左右28位,表示成C0, D0。C0和D0按照循环左移表来分别循环左移,此处是第一次循环,所以循环左移1次,生成C1和D1。然后C1和D1合并成56位密钥经过PC-2置换压缩成48位的K1。
K2的生成过程:C1和D1分别循环左移1次,然后合并经过PC-2置换压缩成K2。Ki的生成就为Ci-1和Di-1分别循环左移,然后合并经过PC-2置换压缩而成。
PC-1 置换表 PC-2置换表 循环左移表
//PC-1置换表
private int[] PC1={
57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4};
//PC-2置换表
private int[] PC2={
14,17,11,24,1,5,3,28,
15,6,21,10,23,19,12,4,
26,8,16,7,27,20,13,2,
41,52,31,37,47,55,30,40,
51,45,33,48,44,49,39,56,
34,53,46,42,50,36,29,32};
//循环左移次数表
private int[] leftTable = {1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1};
F函数的原理
F函数的内部还是比较复杂,不过问题不大。我们按照F函数内部执行顺序来可以分为以下几步:
- Ri-1做一个E扩展,从32位扩展成48位
- Ri-1与Ki异或运算,然后将异或运算的结果经过S盒选择压缩成32位
- 从S盒出来的32位结果再经过P置换,就得到最终的32位Ri
Ri-1做扩散选择的表如下:
//E扩展
private int[] ETable={
32,1,2,3,4,5,
4,5,6,7,8,9,
8,9,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,1};
从S盒出来的32位结果经过的P表如下:
//P置换
private int[] P={
16,7,20,21,29,12,28,17,
1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,
19,13,30,6,22,11,4,25};
在这三步中最为机密的就是S盒的选择压缩了。S盒是如何实现选择压缩呢?我们就要知道S的结构了。
S盒的结构

我们可以看出,进入S盒后将Ri-1与Ki异或的值分成8组,每组6位,分别进入S1-S8盒,然后从每个盒中出4位,合并成32位的结果。
若是还想探究6位变成4位是如何的变换的,就需要看下面这点介绍:
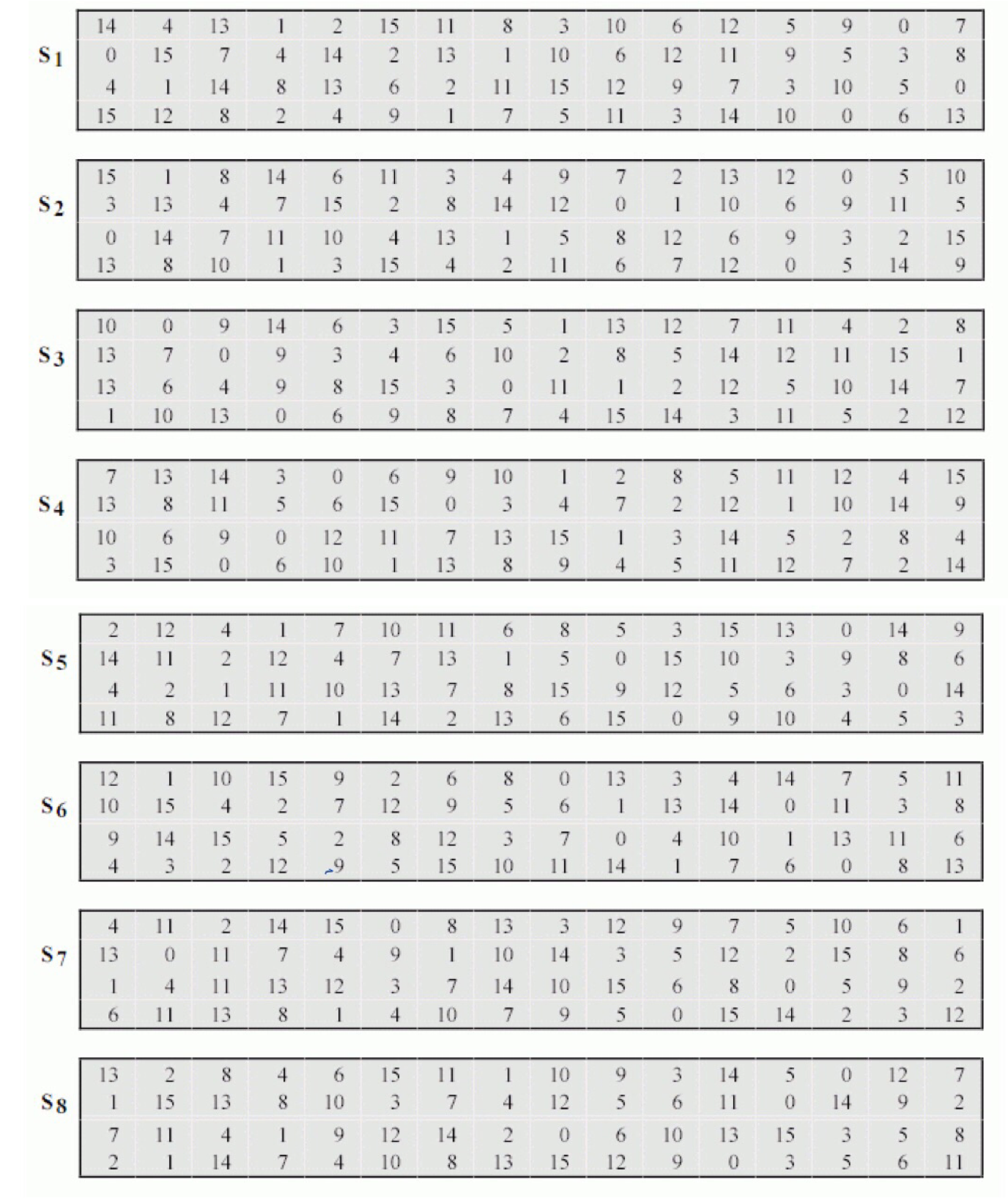
我们以进入S!盒为例,假设进入的6位二进制数为101001,我们一般将第一位和最后一位(从左到右)作为行坐标,中间四位作为纵坐标找值。11即3行,0100即4列(从0开始编号),最后选出的值就为4,四位二进制表示则为0100。
16次的迭代加密
最初我们需要将初始的明文做一个IP置换,然后分成左右各32位即L0 R0,带入L0、R0去计算L1和R1。
16次迭代的规律为:
Li = Ri-1
Ri = Li-1 ^ F(Ri-1, Ki)
最后,L16与R16直接交换赋给L17和R17(L17=R16, R17=L16),然后L17与R17合并后通过IP逆置换生成最终的密文。
以上,便是加密过程,解密可以说是加密的逆向过程。解密为何反向就可以解密,还需要各位看官另觅资料~
DES算法Java实现(完整)
package symmetricipher;
/**
* @description: 代码实现Des算法加解密
* @author sakura
* @date 2019年3月25日 下午12:52:21
*/
/*
* 1.主要的一个迭代公式 Li=Ri Ri = Li-1 ⊕F(Li-1,Ki)
* 2.整体可以分为 加解密运算 F函数的处理 子密钥的产生
* 3.子秘钥产生:64位经过PC-1密钥置换成56位 分为Ci Di左右各28为位 然后根据循环左移表来左移 最后经过PC-2置换成48位的密钥Ki
* 4.F函数的处理:Li-1(32位)经过E盒扩展成48位; 48位的Li-1与 子秘钥Ki进行异或 ;
* 异或的结果经过S盒(8个盒子 6进4出)生成32位;32位再经过P盒转换成最后32位F函数处理后的结果
* 5.加解密运算这边:先将明文做一个IP置换,然后将64位分成左右32位L0,R0 然后开始迭代 ;到第16次,做IP逆置换生成最终的密文
*
* 6.解密运算:
* 加密反过来
*
*/
public class DES {
//初始IP置换
private int[] IP={
58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,
64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7};
//IP逆置换
private int[] IP1={
40,8,48,16,56,24,64,32,
39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,
37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,
35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,
33,1,41,9,49,17,57,25};
//E扩展
private int[] ETable={
32,1,2,3,4,5,
4,5,6,7,8,9,
8,9,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,1};
//P置换
private int[] P={
16,7,20,21,29,12,28,17,
1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,
19,13,30,6,22,11,4,25};
//S盒
private static final int[][][] SBox = {
{
{ 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 },
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 },
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 },
{ 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 } },
{
{ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 },
{ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 },
{ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 },
{ 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 } },
{
{ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 },
{ 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 },
{ 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 },
{ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 } },
{
{ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 },
{ 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 },
{ 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 },
{ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 } },
{
{ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 },
{ 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 },
{ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 },
{ 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 } },
{
{ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 },
{ 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 },
{ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 },
{ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 } },
{
{ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 },
{ 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 },
{ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 },
{ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 } },
{
{ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 },
{ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 },
{ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 },
{ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } }
};
//PC-1置换表
private int[] PC1={
57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4};
//PC-2置换表
private int[] PC2={
14,17,11,24,1,5,3,28,
15,6,21,10,23,19,12,4,
26,8,16,7,27,20,13,2,
41,52,31,37,47,55,30,40,
51,45,33,48,44,49,39,56,
34,53,46,42,50,36,29,32};
//循环左移次数表
private int[] leftTable = {1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1};
//加密轮数16轮
private static final int LOOP = 16;
private String[] keys = new String[LOOP];
private String[] pContent;
private String[] cContent;
private int originLength; //初始明文长度
//16个子密钥
private int[][] subKey = new int[16][48]; //存储16次的子密钥
private String content;
private int pOriginLegth; //明文初始长度?
//构造函数
public DES(String key, String content) {
this.content = content;
pOriginLegth = content.getBytes().length;
generateSubKey(key);
}
//主函数入口
public static void main(String[] args) {
String plainText = "SakuraOne";
System.out.println("明文: \n" + plainText);
String key = "IAMKEY";
DES des = new DES(key,plainText);
byte[] c = des.group(plainText.getBytes(), true);//加密
System.out.println("密文:\n" + new String(c));
byte[] p = des.group(c, false); //解密
byte[] pd = new byte[plainText.getBytes().length];
System.arraycopy(p, 0, pd, 0, plainText.getBytes().length);
System.out.println("解密后的明文:\n" + new String(pd));
}
/**
*拆分分组
*/
public byte[] group(byte[] plainText, boolean decryption) {
//填充明文长度为64位的整数
originLength = plainText.length;
int gNum;
int rNum;
gNum = originLength/8;
rNum = 8-(originLength-gNum*8);
byte[] pPadding;
if(rNum<8) {
pPadding = new byte[originLength+rNum];
System.arraycopy(plainText, 0, pPadding, 0, originLength);
for(int i=0; i<rNum; i++) {
pPadding[originLength+1]=(byte)rNum;
}
}else {
pPadding = plainText;
}
gNum = pPadding.length/8;
byte[] groupPT = new byte[8]; //64位分组单位
byte[] resultData = new byte[pPadding.length];
for(int i=0; i<gNum; i++) {
System.arraycopy(pPadding, i*8, groupPT, 0, 8);
System.arraycopy(encryptUnit(groupPT, subKey, decryption), 0, resultData, i*8, 8);
}
//如果是解密 这里感觉什么也没有做呢??
if(decryption == false) {
byte[] pResultData = new byte[pOriginLegth];
System.arraycopy(resultData, 0, pResultData, 0, pOriginLegth);
return pResultData;
}
return resultData;
}
/**
*加密一个64位分组
*
*/
public byte[] encryptUnit(byte[]unit, int keysArray[][], boolean decryption) {
//得到明文的01字符串
StringBuilder sb = new StringBuilder();
for(int i=0; i<8; i++) {
String tmpBit = Integer.toBinaryString(unit[i] & 0xff);
while(tmpBit.length()%8!=0) {
tmpBit="0"+tmpBit;
}
sb.append(tmpBit);
}
//将明文01字符串转换为数字01存放在数组中
int[] pBit = new int[64];
String pStr = sb.toString();
for(int i=0; i<64; i++) {
int bit = Integer.valueOf(pStr.charAt(i));
if(bit == 48) {
bit = 0;
}else if(bit == 49){
bit = 1;
}else {
System.out.println("To bit error");
}
pBit[i] = bit;
}
/*=========IP置换==========*/
int[] pIP = new int[64];
for(int i=0; i<64; i++) {
pIP[i] = pBit[IP[i]-1];
}
//加密
if(decryption) {
//迭代16次
for(int i=0; i<16; i++) {
loop(pIP, i, decryption, keysArray[i]);
}
}else { //解密 反向迭代
for(int i=15; i>-1; i--) {
loop(pIP, i, decryption, keysArray[i]);
}
}
/*===========IP逆置换=============*/
int[] c = new int[64];
for(int i=0; i<IP1.length; i++) {
c[i] = pIP[IP1[i]-1];
}
byte[] cByte = new byte[8];
for(int i=0; i<8; i++) {
cByte[i] = (byte)((c[8*i]<<7)+(c[8*i+1]<<6)+(c[8*i+2]<<5)+(c[8*i+3]<<4)+(c[8*i+4]<<3)+(c[8*i+5]<<2)+(c[8*i+6]<<1)+(c[8*i+7]));
}
return cByte; //最终的密码字节数组
}
//依次迭代过程
public void loop(int[] median, int times, boolean decryption, int[]keyArray ) {
int[] l0 = new int[32];
int[] r0 = new int[32];
int[] l1 = new int[32];
int[] r1 = new int[32];
int[] f = new int[32]; //调用F函数后生成的结果
System.arraycopy(median, 0, l0, 0, 32);
System.arraycopy(median, 32, r0, 0, 32);
l1 = r0;
f = fFunction(r0, keyArray); //调用F函数
for(int i=0; i<32; i++) {
r1[i] = l0[i]^f[i]; //ri = li-1 ^ f[i]
if(((decryption==false) && (times==0)) || ((decryption==true) && (times==15))) {
median[i] = r1[i];
median[i+32] = l1[i];
}else {
median[i] = l1[i];
median[i+32] = r1[i];
}
}
}
/**
* F函数
*/
public int[] fFunction(int[] rContent, int[] key) {
int[] result = new int[32];
int[] rXORkey = new int[48];
//ri扩展 与 keyi异或
for(int i=0; i<ETable.length; i++) {
rXORkey[i] = rContent[ETable[i]-1]^key[i];
}
/*=============S-box替换 将48位变成32位==============*/
int[][] s= new int[8][6];
int[] sAfter = new int[32];
for(int i=0; i<8; i++) {
System.arraycopy(rXORkey, i*6, s[i], 0, 6);
int r = (s[i][0]<<1)+s[i][5]; //横坐标
int c = (s[i][1]<<3) + (s[i][2]<<2) + (s[i][1]<<1) + s[i][4]; //纵坐标
String str = Integer.toBinaryString(SBox[i][r][c]);
while(str.length() < 4) {
str = "0"+str;
}
for(int j=0; j<4; j++) {
int p=Integer.valueOf(str.charAt(j));
if(p==48) {
p=0;
}else if(p==49) {
p=1;
}else {
System.out.println("To bit error!");
}
sAfter[4*i+j] = p;
}
}
/*===============P盒替换=====================*/
for(int i=0; i<P.length; i++) {
result[i] = sAfter[P[i]-1];
}
return result;
}
/**
* description:生成子密钥
*
* @param key 密钥
*
*/
public void generateSubKey(String key) {
//当key的长度小于64位时要扩展至64位
while(key.length()<8) {
key = key + key;
}
key = key.substring(0, 8);
//将字符密钥转换成二进制形式
byte[] keys = key.getBytes();
int[] kBit = new int[64];
for(int i=0; i<8; i++) {
//每个字节即每8位&0000 0000
String kStr = Integer.toBinaryString(keys[i] & 0xff);
//补齐8位
if(kStr.length()<8) {
for(int t=0; t<8-kStr.length(); t++) {
kStr = "0" + kStr;
}
}
//将01字符串转换成二进制01
for(int j=0; j<8; j++) {
int p = Integer.valueOf(kStr.charAt(j));
if(p == 48) {
p=0;
}else if(p == 49) {
p=1;
}else {
System.out.println("To bit error!");
}
kBit[i*8+j] = p;
}
}
//得到kBit 初始化的64位密钥 然后进行PC-1压缩成56位
/*==============PC-1压缩===============*/
int[] kNewBit = new int[56];
for(int i=0; i<PC1.length; i++) {
kNewBit[i] = kBit[PC1[i]-1];
}
/*================初始密钥分组=============*/
int[] c0 = new int[28];
int[] d0 = new int[28];
System.arraycopy(kNewBit, 0, c0, 0, 28);
System.arraycopy(kNewBit, 28, d0, 0, 28);
//生成16个子密钥
for(int i=0; i<16; i++) {
int[] c1 = new int[28];
int[] d1 = new int[28];
/*============ci、di分别循环左移===========*/
if(leftTable[i] == 1) {
System.arraycopy(c0, 1, c1, 0, 27);
c1[27]=c0[0];
System.arraycopy(d0, 1, d1, 0, 27);
d1[27]=d0[0];
}else if(leftTable[i] == 2) {
System.arraycopy(c0, 2, c1, 0, 26);
c1[26]=c0[0];
c1[27]=c0[1];
System.arraycopy(d0, 2, d1, 0, 26);
d1[26]=d0[0];
d1[27]=d0[1];
}else {
System.out.println("leftTable error!");
}
/*================ci、di合并 PC-2压缩置换=============*/
int[] tmp = new int[56];
System.arraycopy(c1, 0, tmp, 0, 28);
System.arraycopy(d1, 0, tmp, 28, 28);
for(int j=0; j<PC2.length; j++) {
subKey[i][j] = tmp[PC2[j]-1];
}
c0 = c1;
d0 = d1;
}
}
}

小结
这学期在上密码学的课程,课堂上听老师讲了对称加密算法中的DES算法,一直觉得挺绕。在上完实验课后勉强对其算法流程有了一个清晰认识。后面想着用算法实现或许会更明了, 于是写代码实现。确实,自己实现一遍后对算法会更理解。粗糙地记录了下DES加解密的实现,以供参考。解密算法的验证需要大家另觅资料,本篇博文就不再介绍了~
参考:
DES算法原理与Java实现https://blog.csdn.net/android_jiangjun/article/details/79654940


