有限元分析 ANSYS理论与应用(第4版).例3.1_MATLAB理论求解

相关帖子：

有限元分析 ANSYS理论与应用(第4版).例3.1_ANSYS.APDL求解

有限元分析 ANSYS理论与应用(第4版).例3.1_ANSYS.Workbench求解

题目描述：

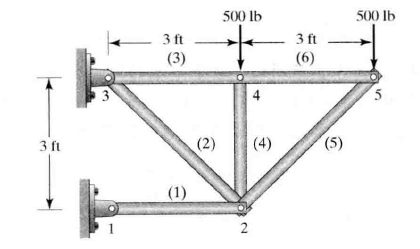
如图所示阳台桁架及其尺寸。假设所有杆件均为木质材料（道格拉斯红杉），弹性模量E=1.9×106lb/in2，且且面积为8in2。确定每个接头的挠度，以及每个杆件的平均应力。下面将MATLAB求解这个问题。

image

 

1、将问题结构离散为节点和单元：桁架的每个杆件作为单元，每个杆件的连接点作为节点。因此，给定的桁架可以用5个节点和6个单元进行建模。其中：1ft=12in.

Element Node i Node j Length
（in.）		 A
（in2）		 E
（lb/in2）		 θ
（°)
1 1 2 36.0 8 1.9E+06 0
2 2 3 50.9 8 1.9E+06 135
3 3 4 36.0 8 1.9E+06 0
4 2 4 36.0 8 1.9E+06 90
5 2 5 50.9 8 1.9E+06 45
6 4 5 36.0 8 1.9E+06 0
 
2、计算各个单元的刚度矩阵，建立整体矩阵，边界条件处理，刚度方程及未知位移求解，求解支反力
%% 定义输入条件
A = 8; %杆件截面积
E = 1.9E6; % 杆件材料弹性模量
L1 = 36; % 1、3、4、6号杆件的长度
L2 = 50.9; % 2、5号杆件的长度

%% 计算单元刚度矩阵
k1 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵
k2 = Bar2D2Node_Stiffness(E, A, L2, 135); %计算单元1刚度矩阵
k3 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵
k4 = Bar2D2Node_Stiffness(E, A, L1, 90); %计算单元1刚度矩阵
k5 = Bar2D2Node_Stiffness(E, A, L2, 45); %计算单元1刚度矩阵
k6 = Bar2D2Node_Stiffness(E, A, L1, 0); %计算单元1刚度矩阵

%% 建立整体刚度矩阵
kk = zeros(10, 10);
kk = Bar2D2Node_Assembly(kk, k1, 1, 2);
kk = Bar2D2Node_Assembly(kk, k2, 2, 3);
kk = Bar2D2Node_Assembly(kk, k3, 3, 4);
kk = Bar2D2Node_Assembly(kk, k4, 2, 4);
kk = Bar2D2Node_Assembly(kk, k5, 2, 5);
kk = Bar2D2Node_Assembly(kk, k6, 4, 5) % 输出整体刚度矩阵

%% 边界条件处理
k = kk([3 4 7 8 9 10], [3 4 7 8 9 10]);%添加位移约束。即应用边界条件：节点1、3的位移为0，即消去1、2、5、6的行列，仅仅提取不连续的行列
pp = [0; 0; 0; 0; 0; 0; 0; -500; 0; -500];%添加外载荷
p = pp([3 4 7 8 9 10]);%添加位移约束。应用边界条件：节点1、3的位移为0，即消去1、2、5、6的行列，仅仅提取不连续的行列

%% 求解阶段
u = k\p;%求解边界未知位移

%% 支反力计算
U = [0; 0; u(1, 1); u(2, 1); 0; 0; u(3, 1); u(4, 1); u(5, 1); u(6, 1)]%组装整体位移矩阵
F = kk*U %求解载荷矩阵F
R = F - pp %求解支反力R

 

3、输出结果

kk =

   1.0e+05 *

    4.2222  0 -4.2222       0       0       0       0       0       0       0
         0  0       0       0       0       0       0       0       0       0
   -4.2222  0  7.2085  0.0000 -1.4931  1.4931 -0.0000 -0.0000 -1.4931 -1.4931
         0  0  0.0000  7.2085  1.4931 -1.4931 -0.0000 -4.2222 -1.4931 -1.4931
         0  0 -1.4931  1.4931  5.7153 -1.4931 -4.2222       0       0       0
         0  0  1.4931 -1.4931 -1.4931  1.4931       0       0       0       0
         0  0 -0.0000 -0.0000 -4.2222       0  8.4444  0.0000 -4.2222       0
         0  0 -0.0000 -4.2222       0       0  0.0000  4.2222       0       0
         0  0 -1.4931 -1.4931       0       0 -4.2222       0  5.7153  1.4931
         0  0 -1.4931 -1.4931       0       0       0       0  1.4931  1.4931


U =

         0
         0
   -0.0036
   -0.0102
         0
         0
    0.0012
   -0.0114
    0.0024
   -0.0195


F =

   1.0e+03 *

    1.5000
         0
    0.0000
    0.0000
   -1.5000
    1.0000
   -0.0000
   -0.5000
    0.0000
   -0.5000


R =

   1.0e+03 *

    1.5000
         0
    0.0000
    0.0000
   -1.5000
    1.0000
   -0.0000
         0
    0.0000
         0

 

4、附录

------------------------------Bar2D2Node_Stiffness----------------------------
function k = Bar2D2Node_Stiffness(E, A, L, D)
%计算单元的刚度矩阵
%输入弹性模量E, 横截面积A, 杆长L, 杆与X轴的角度D（°）
%输出单元刚度矩阵k
D = D*pi/180;
k = E*A/L*[
     cos(D)*cos(D),  sin(D)*cos(D), -cos(D)*cos(D), -sin(D)*cos(D);
     sin(D)*cos(D),  sin(D)*sin(D), -sin(D)*cos(D), -sin(D)*sin(D);
    -cos(D)*cos(D), -sin(D)*cos(D),  cos(D)*cos(D),  sin(D)*cos(D);
    -sin(D)*cos(D), -sin(D)*sin(D),  sin(D)*cos(D),  sin(D)*sin(D); ];
--------------------------Bar2D2Node_Assembly---------------------------------
function z = Bar2D2Node_Assembly(kk, k, i, j)
% 以上函数进行单元刚度矩阵的组装
% 输入整体刚度矩阵kk（初始为0矩阵）, 单元刚度矩阵k, 单元的节点编号i，j
% 输出整体刚度矩阵kk
DOF(1) = 2*i-1;
DOF(2) = 2*i;
DOF(3) = 2*j-1;
DOF(4) = 2*j;
for n1 = 1:4
    for n2 = 1:4
        kk(DOF(n1), DOF(n2)) = kk(DOF(n1), DOF(n2)) + k(n1, n2);
    end
end
z=kk;

posted on 2019-10-31 19:52  损先森  阅读(1521)  评论(0)  编辑  收藏  举报

导航