需求背景、限制条件、化简
汉诺塔就是一个由柱子和盘子组成的玩具，它有一些玩法上的限制，主要是规定了盘子移动有限制。
想理解到递归本质，汉诺塔是个不错的载体。
怎么体会?
在盘子移动的过程中。
# 盘子的数量：
# 通常，我们假设有 n 个盘子。盘子在初始时按从大到小的顺序叠放在一个柱子上（源柱子）。
# 这里采用数字表示盘子，数字大小表示盘子大小。
# 柱子数量：
# 总共有三个柱子：源柱子（起始柱子）、目标柱子（最终柱子） 和辅助柱子（中间柱子）。
# 这里用a,b,c list模拟三个柱子
# 规定list只能从末尾取出
# 移动规则：
# 每次只能移动一个盘子。
# 任何时刻盘子只能放在一个柱子上。
# 大的盘子不能放在小的盘子上。
# 目标：
# 将所有的盘子从源柱子移动到目标柱子，且遵守上述规则。
总结：
- 了解了问题和目标；
- 将现实问题抽出，化简，采用符号化方式去表达；
模拟盘子的移动步骤
先正常演示一次移动：
n = 1
a = [1]
b = []
c = []
a = []
b = []
c = [1]
n = 2
a = [2,1]
b = []
c = []
(1)
a = [2]
b = [1]
c = []
(2)
a = []
b = [1]
c = [2]
(3)
a = []
b = []
c = [2,1]
**
n = 3
a = [3,2,1]
b = []
c = [1]
(1)
a = [3,2]
b = []
c = [1]
(2)
a = [3]
b = [2]
c = [1]
(3)
a = [3]
b = [2,1]
c = []
(4)
a = []
b = [2,1]
c = [3]
(5)
a = [1]
b = [2]
c = [3]
(6)
a = [1]
b = []
c = [3,2]
(7)
a = []
b = []
c = [3,2,1]
上面正向的思考，n约大，步骤越多，越来越乱, 抓不住重点。
必须得以反向思维思考：
n = 3
a = [3]
b = [2,1]
c = []
a = []
b = [2,1]
c = [3]
**
n = 4
a = [4]
b = [3,2,1]
c = []
a = []
b = [3,2,1]
c = [4]
**
n = 5
a = [5]
b = [4,3,2,1]
c = []
a = []
b = [4,3,2,1]
c = [5]
......
简单的抓到一些固定特征：
-
不管n是几，都是a到c.
-
如果n>1，就把n-1的盘子都放到辅助柱子，n 直接去 c。（这个也是划分出来的一个子问题）
递归实现Code
def hanoi(n: int, a: list, b: list, c: list):
print("sub State:", a, b, c)
if n == 1:
# 基准情况
c.append(a.pop())
print("State 1:", a, b, c)
else:
# 递归情况
hanoi(n - 1, a, c, b)
c.append(a.pop())
print("State 2:", a, b, c)
hanoi(n - 1, b, a, c)
a = [3, 2, 1]
b = []
c = []
print("Initial state:", a, b, c)
hanoi(len(a), a, b, c)
print("Final state:", a, b, c)
核心：
在递归调用中，柱子的角色（源、目标、辅助）不断交换。这种角色交换保证了每一步都能正确地完成盘子的移动。
out:
Initial state: [3, 2, 1] [] []
sub State: [3, 2, 1] [] []
sub State: [3, 2, 1] [] []
sub State: [3, 2, 1] [] []
State 1: [3, 2] [] [1]
State 2: [3] [1] [2]
sub State: [1] [3] [2]
State 1: [] [3] [2, 1]
State 2: [] [2, 1] [3]
sub State: [2, 1] [] [3]
sub State: [2, 1] [3] []
State 1: [2] [3] [1]
State 2: [] [1] [3, 2]
sub State: [1] [] [3, 2]
State 1: [] [] [3, 2, 1]
Final state: [] [] [3, 2, 1]
分析
采用可视化方式观察：
https://pythontutor.com/
看完的的一些体会：
-
函数会嵌套函数, 多个嵌套函数之间一起组成一个整体的函数；
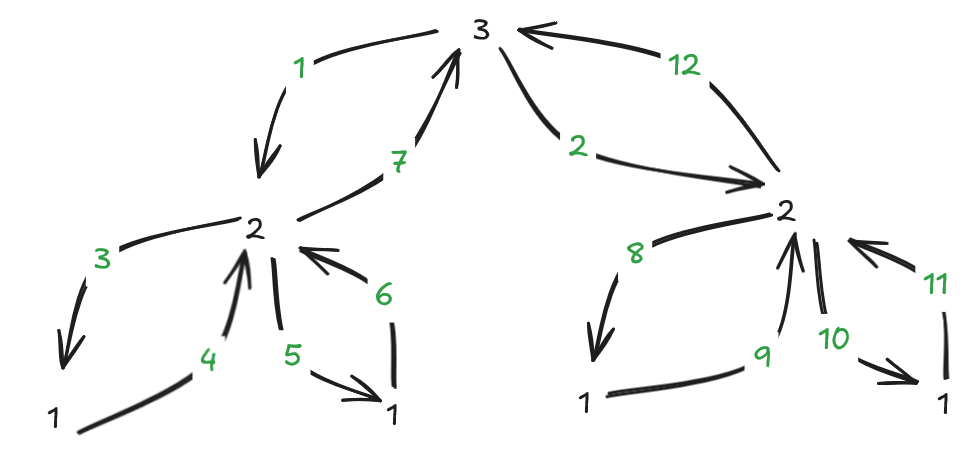
在函数里面调用了2次自身，就会在下一个节点分出两次。
思考：如果调用了3次自身，会分成出去3次吗？
如果调用了2次自身，感觉都会把程序弄得很复杂。 -
递归通过传递下去的变量，在去 回之间的改变，能达到一个很炸裂的效果；
-
递归的层下沉，一般使用一个int变量控制。
练习 1
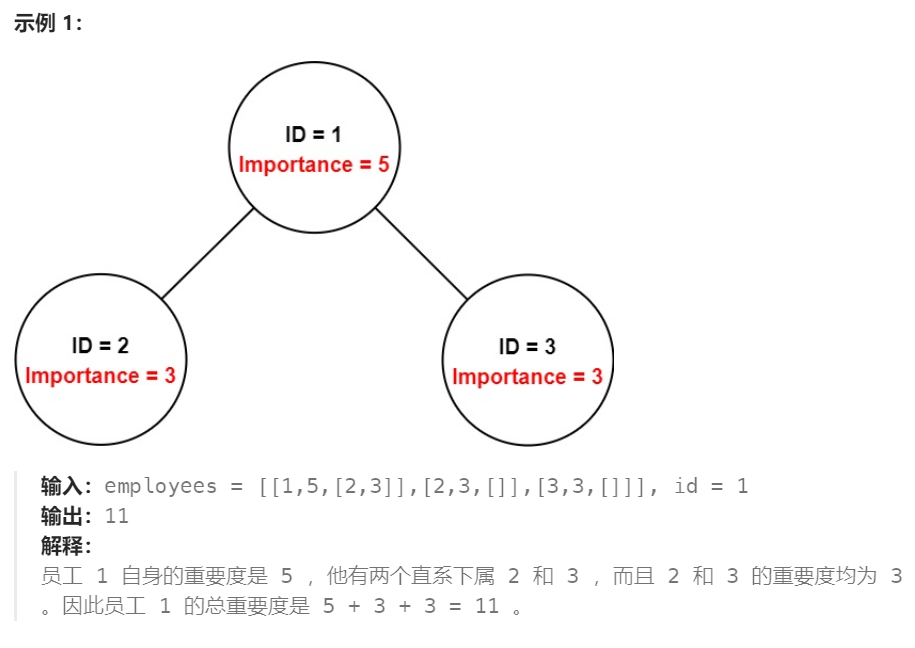
你有一个保存员工信息的数据结构，它包含了员工唯一的 id ，重要度和直系下属的 id 。
给定一个员工数组 employees，其中：
- employees[i].id 是第 i 个员工的 ID。
- employees[i].importance 是第 i 个员工的重要度。
- employees[i].subordinates 是第 i 名员工的直接下属的 ID 列表。
给定一个整数 id 表示一个员工的 ID，返回这个员工和他所有下属的重要度的 总和。
# Definition for Employee.
class Employee:
def __init__(self, id: int, importance: int, subordinates: List[int]):
self.id = id
self.importance = importance
self.subordinates = subordinates
