图结构 (英文:Graph Structure)
图的定义:
在数据的逻辑结构中,如果结构中的某一个节点的前驱和后继的个数不加限制,则称这种数据结构为图结构(图形结构、Graph)。
图形结构是一种比树形结构更复杂的非线性结构。区别在于:
- 在树形结构中,结点间具有分支层次关系,每一层上的结点只能和上一层中的至多一个结点相关,但可能和下一层的多个结点相关。
- 而在图形结构中,任意两个结点之间都可能相关,即结点之间的邻接关系可以是任意的。
图的应用场景
网络安全:
利用图数据模型可以表示网络中的实体(如用户、设备、网络节点)及其之间的复杂关系,从而更好地分析网络安全威胁、检测网络攻击和异常行为。例如,可以利用图数据库存储网络设备之间的连接关系、用户之间的交互行为等,通过对图数据的查询和分析,发现潜在的网络攻击路径和恶意行为。
金融风控:
金融领域中存在大量的实体和关系数据,如用户、账户、交易、资产等。利用图数据库可以将这些实体和关系以图的形式存储和管理,便于进行风险评估、欺诈检测、信用评级等任务。
例如,通过对用户之间的社交关系、交易行为的分析,可以发现潜在的欺诈行为和风险交易。
社交网络:
社交网络中的用户、好友关系、兴趣标签等可以抽象为图数据,利用图数据库可以快速查询和分析社交网络中的用户关系、兴趣匹配、信息传播等。
例如,可以利用图数据库存储用户之间的社交关系,通过对图数据的查询和分析,发现用户之间的共同兴趣和社交网络中的影响力节点。
生物医学:
生物医学领域中的分子结构、蛋白质相互作用、基因组数据等可以表示为图数据。利用图数据库可以存储和管理这些图数据,便于进行药物研发、疾病诊断、基因分析等任务。
例如,通过对分子结构的图数据进行分析,可以发现药物分子的潜在活性和副作用。
推荐系统:
推荐系统中的用户、物品、兴趣等可以表示为图数据,利用图数据库可以存储和管理这些图数据,进行个性化推荐、用户兴趣挖掘等任务。
例如,通过对用户兴趣的图数据进行分析,可以发现用户的潜在兴趣和推荐相似的物品。
以上是图的应用场景的简要介绍,图数据库在处理复杂的实体关系和关联数据时具有优势,能够有效地存储、查询和分析大规模的图数据。
图的概念和分类
-
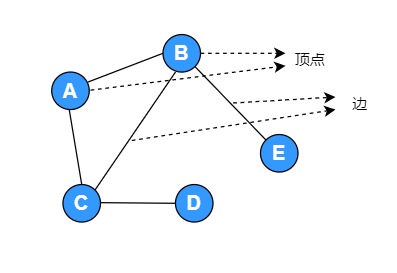
顶点(也叫点、节点):A、B、C、...
-
边(也称作弧):顶点和顶点之间的连线
-
无向图:边没有方向的图称为无向图

-
有向图:顶点和顶点之间的边有方向

-
带权图:边带有权值,权值指的是边的值

-
无向无权图
-
无向有权图
-
有向无权图
-
有向带权图
-
重图
定义:重图,也称多重图(multigraph)或伪图(pseudograph)是一个允许有重边(也称多重边,平行边)的图。重边即两个顶点之间可能存在多条边。

注:含有多重边(红色)和自环(蓝色)的多重图。并非所有的多重图都允许包含自环。 -
...
图的操作
存储
图的存储方式有:
1. 邻接表(链表)(本文就演示这种方式,其它方式可以自己操作一下)
2. 邻接矩阵(就是二维数组, 这个方式也会简单演示)
3. 关联矩阵
4. 邻接多重表
5. 十字链表等....
(不同的存储结构,在不同地特定的场景下可能更加适用。选择合适的存储方式取决于图的类型、规模以及需要进行的操作。)
邻接矩阵演示:
邻接矩阵是图的常用存储表示,它的底层依赖一个二维数组。它用两个数组分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。
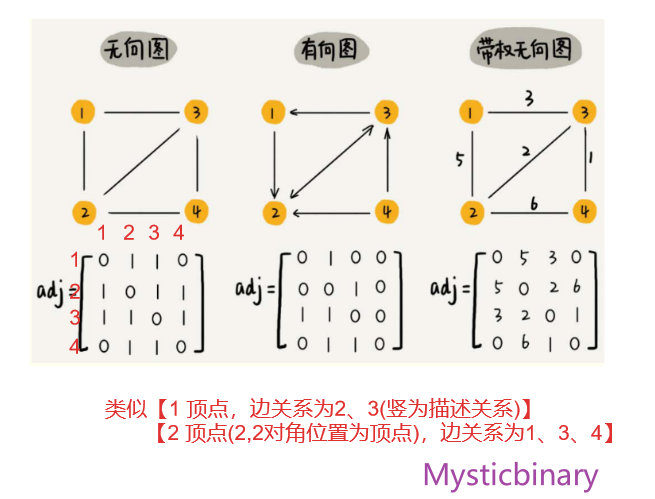
对于无向图的描述,a[i][j] == a[j][i],我们只需要存储一个就好,在二维数组中,通过对角线可以划分为两部分,我们只要利用其中一部分的空间就可以了,另外一部分则是多余的。
存储的是稀疏图(Sparse Matrix):顶点很多,但每个顶点的边并不多,邻接矩阵的存储方法就更加浪费空间了。可以采用邻接表。
优点:
- 邻接矩阵的存储方式简单、直接,可以高效的获取两个顶点的关系;
- 计算方便。(求解最短路径 Floyd-Warshall 算法)。
缺点:
- 虽然用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。
邻接表演示:
定义结构体
package graph;
import java.awt.*;
import java.util.*;
import javax.swing.*;
class Graph extends JPanel {
//adjacencyList 充当了存储图结构信息的核心数据结构的角色。通过对它进行操作,我们就可以构建和表示给定的图。
//adjacencyList 使用HashMap和LinkedList实现了邻接表的数据结构 ,思考为什么不用ArrayList?
/**
* adjacencyList 是这个代码中定义的一个 HashMap<String, LinkedList<String>> 类型的成员变量,用于表示图的邻接表数据结构。
* <p>
* 在图论中,邻接表是一种常用的存储图的方式。对于每个节点,我们使用一个链表来存储与该节点相邻的节点
* 在这个实现中,adjacencyList 的:
* 键(key)是节点的标签(String类型)
* 值(value)是一个 LinkedList<String>对象,表示与该节点相邻的所有节点的标签列表。
* <p>
* 例如,对于图中的节点 A,它与 B 和 C 相邻,那么 adjacencyList 中就会有一个条目:
* "A" -> ["B", "C"]
* <p>
* <p>
* 这样,我们就可以通过查询 adjacencyList.get("A") 来获取与节点 A 相邻的所有节点的列表。
* <p>
* 使用邻接表来表示图有以下优点:
* 1.方便存储无序的、不连续的边信息。
* 2.对于稀疏图(边的数量远小于节点数量的平方)来说,邻接表比邻接矩阵更节省空间。
* 3.添加或删除边的操作比较简单和高效。
*/
private HashMap<String, LinkedList<String>> adjacencyList;
public Graph() {
adjacencyList = new HashMap<>();
// 添加节点
addNode("A");
addNode("B");
addNode("C");
addNode("D");
addNode("E");
// 添加边
addEdge("A", "B");
addEdge("A", "C");
addEdge("B", "C");
addEdge("B", "E");
addEdge("C", "D");
}
//addNode方法用于添加节点
public void addNode(String label) {
adjacencyList.putIfAbsent(label, new LinkedList<>());
}
//addEdge方法用于添加边
//addEdge的功能是向邻接表中添加两个顶点之间的边。
public void addEdge(String source, String destination) {
// 首先检查 source 和 destination 节点是否都存在于 adjacencyList 中。
// 如果有任何一个节点不存在,则不执行后续操作,因为我们不能在不存在的节点之间添加边。
if (adjacencyList.containsKey(source) && adjacencyList.containsKey(destination)) {
//如果两个节点都存在,则执行以下步骤:
//这一行代码获取与 source 节点相关联的邻接表(LinkedList<String>),并将 destination 节点的标签添加到该邻接表中。这表示从 source 节点出发,可以到达 destination 节点。
adjacencyList.get(source).add(destination);
// 这一行代码获取与 destination 节点相关联的邻接表,并将 source 节点的标签添加到该邻接表中。这表示从 destination 节点出发,也可以到达 source 节点。
adjacencyList.get(destination).add(source);
}
/**
* 这段代码的目的是在无向图中添加一条边。由于无向图的边是双向的,因此需要在两个节点的邻接表中都添加对方的节点标签。
*
* 例如,如果我们执行 addEdge("A", "B")操作,则在 adjacencyList 中会有以下的更新:
* "A" -> ["B"]
* "B" -> ["A"]
* 这表示节点 A 和节点 B 之间存在一条边,它们是相互可达的。
*/
}
//查询指定节点的相邻节点
public void queryNode(String label) {
if (adjacencyList.containsKey(label)) {
System.out.print("Node " + label + " is connected to: ");
for (String neighbor : adjacencyList.get(label)) {
System.out.print(neighbor + " ");
}
System.out.println();
} else {
System.out.println("Node " + label + " does not exist in the graph.");
}
}
// 下面是一些绘图代码,不需要关注,和图结构关系不大。
//在paintComponent方法中,我首先定义了每个节点的位置坐标,然后遍历邻接表,绘制节点和连线。
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
HashMap<String, Point> nodePositions = new HashMap<>();
nodePositions.put("A", new Point(100, 100));
nodePositions.put("B", new Point(300, 50));
nodePositions.put("C", new Point(100, 200));
nodePositions.put("D", new Point(200, 200));
nodePositions.put("E", new Point(400, 200));
for (String node : adjacencyList.keySet()) {
Point pos = nodePositions.get(node);
drawNode(g, node, pos.x, pos.y);
}
for (String source : adjacencyList.keySet()) {
Point sourcePos = nodePositions.get(source);
for (String destination : adjacencyList.get(source)) {
Point destPos = nodePositions.get(destination);
drawLine(g, sourcePos.x, sourcePos.y, destPos.x, destPos.y);
}
}
}
private void drawNode(Graphics g, String label, int x, int y) {
g.setColor(Color.BLUE);
g.fillOval(x - 20, y - 20, 40, 40);
g.setColor(Color.WHITE);
g.drawString(label, x - 5, y + 5);
}
private void drawLine(Graphics g, int x1, int y1, int x2, int y2) {
g.setColor(Color.BLACK);
g.drawLine(x1, y1, x2, y2);
}
/**
* drawNode方法用于绘制一个带标签的圆形节点。
* drawLine方法用于绘制连接两个节点的线段。
* 在main方法中,创建并显示Graph的实例。
*
* @param args
*/
public static void main(String[] args) {
JFrame frame = new JFrame("Graph");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setSize(600, 400);
frame.add(new Graph());
frame.setVisible(true);
}
}
输出:
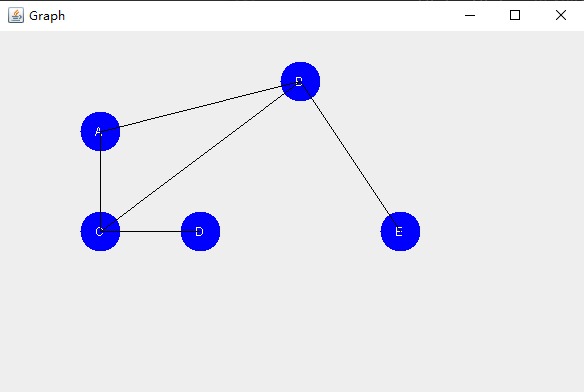
查询
两种遍历方式:
- 深度优先遍历(DFS——Depth First Search)
- 广度优先遍历(BFS——Breath First Search)
只需要大概了解,这里不深度讲解两种遍历方式。
广度优先介绍:
广度优先遍历也叫层序遍历,先遍历第一层(节点 1),再遍历第二层(节点 2,3,4),第三层(5,6,7,8),第四层(9,10)。

深度优先介绍:
从根结点出发,一直向左子节点走,直到左子节点不存在然后返回到上一个节点走这个节点的右子节点,然后一直往右子节点走,同样的也是走不通为止就返回。很显然这种一路走到黑,黑了就回头的方式,就是深度优先遍历的过程。


查询一个节点的相关节点:
这个 queryNode() 方法实际上并不是在执行图的深度优先搜索(DFS)或广度优先搜索(BFS)遍历算法。它只是简单地输出指定节点的所有直接相邻节点,而不涉及对整个图进行遍历。
在这个代码中,我们使用 HashMap 和 LinkedList 构建了一个邻接表来表示图的结构。
对于每个节点,我们使用一个 LinkedList
当调用 queryNode(String label) 时,它会首先检查 label 是否存在于 adjacencyList 中。
如果存在,则直接遍历该节点对应的 LinkedList
这个过程实际上只是对一个线性数据结构(LinkedList)进行了简单的遍历,而不涉及对整个图进行深度或广度优先的系统遍历。
public static void main(String[] args) {
Graph graph = new Graph();
// 查询指定节点的相邻节点
graph.queryNode("B");
}
输出:
Node B is connected to: A C E


 浙公网安备 33010602011771号
浙公网安备 33010602011771号