一个码农在工位上写代码累了,趴着睡着了。
再次睁开眼睛,发现身边好几个妖艳宫女正在给你按摩敲背,住的屋子墙壁和天花板都镶嵌着金箔和银片,大殿的柱子是金丝楠木,雕龙刻凤,地毯是波斯纯手工制作,踩上去柔软而温暖。
突然一个老太监急急忙忙的跑到我跟前说:
“大皇子,皇上驾崩了,得速速从南京回北京继承皇位呀!还有一个重要情报,二皇子已经在南京出发了,意图不轨!”
“这还了得!快拿地图来!”
老太监,缓缓把地图展开,你看着这个图,陷入深深的思考,你需要找到最快的路径。
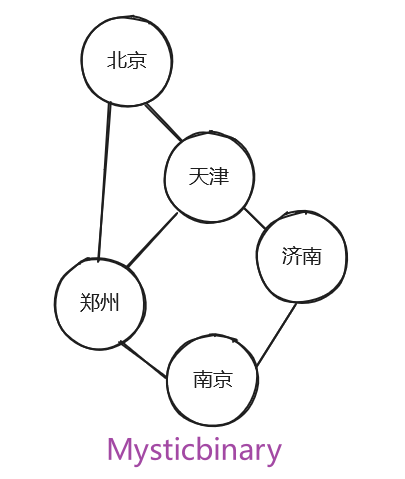
需求:
不考虑路径长短,默认都是1,只考虑节点之间最短的。
初级求解
采用广度优先的思路:
南京 ——> 郑州 ——> 北京 = 3
南京 ——> 郑州 ——> 天津 ——> 北京 = 4
南京 ——> 郑州 ——> 天津 ——> 济南 (死路)
南京 ——> 济南 ——> 天津 ——> 北京 = 4
一眼就知道选3。 当然这个是一个简单图结构,如果是一个复杂的图结构,那么就需要计算机了,计算机是怎么计算图的最短路径呢? 需要了解一下Dijkstra算法。
Dijkstra算法入门
戴克斯特拉算法(英语:Dijkstra's algorithm),又称迪杰斯特拉算法、Dijkstra算法。
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
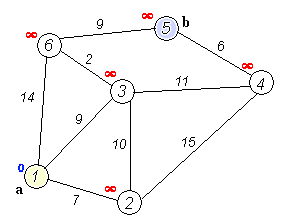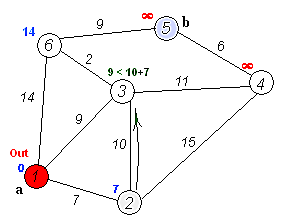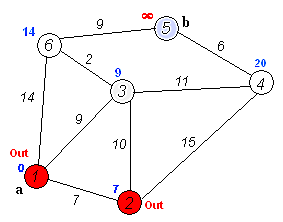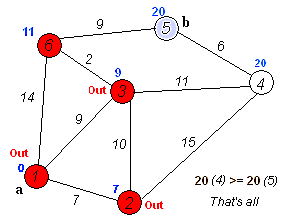
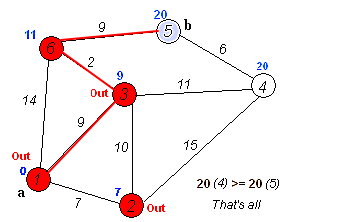
首先设立原点A,目前已知原点A点至A点的距离为0,将其记录在原点上,标记为已探索,其余顶点尚未探索因此皆在该点上标记为为无穷大(∞)。
运行原理:
- 指定一个节点,例如我们要计算 'A' 到其他节点的最短路径;
- 引入两个集合(S、U),
- S集合包含已求出的最短路径的点(以及相应的最短长度);
- U集合包含未求出最短路径的点(以及A到该点的路径,注意 如上图所示,A->C由于没有直接相连 初始时为∞);
- 初始化两个集合,S集合初始时 只有当前要计算的节点,A->A = 0,U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞ ;
- 从U集合中找出路径最短的点,加入S集合,例如 A->D = 2
- 更新U集合路径,if ( 'D 到 B,C,E 的距离' + 'AD 距离' < 'A 到 B,C,E 的距离' ) 则更新U;
- 循环执行 4、5 两步骤,直至遍历结束,得到A 到其他节点的最短路径。
脑中演算:
-
选定A节点并初始化,如上述
步骤3所示,
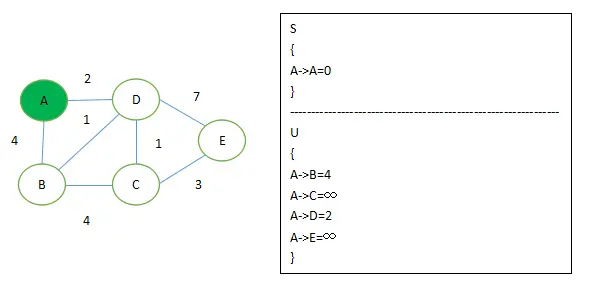
-
执行上述
4、5步骤,找出U集合中路径最短的节点D 加入S集合,并根据条件 if ( 'D 到 B,C,E 的距离' + 'AD 距离' < 'A 到 B,C,E 的距离' ) 来更新U集合,
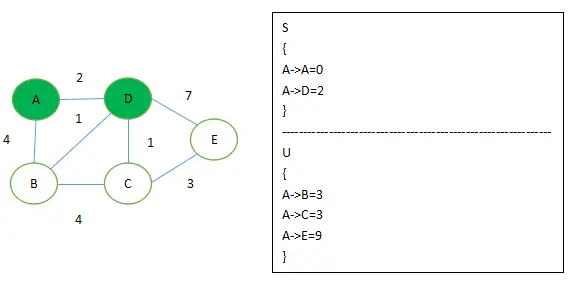
-
这时候 A->B, A->C 都为3,没关系。其实这时候他俩都是最短距离,如果从算法逻辑来讲的话,会先取到B点。而这个时候 if 条件变成了 if ( 'B 到 C,E 的距离' + 'AB 距离' < 'A 到 C,E 的距离' ) ,如图所示这时候A->B距离 其实为 A->D->B
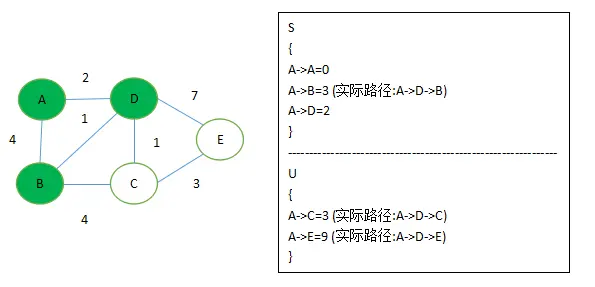
我补充了一个图, 只要记住,只要最短路径S集合里面有的,都会走一次遍历,就能想明白:

-
思路就是这样,往后就是循环了
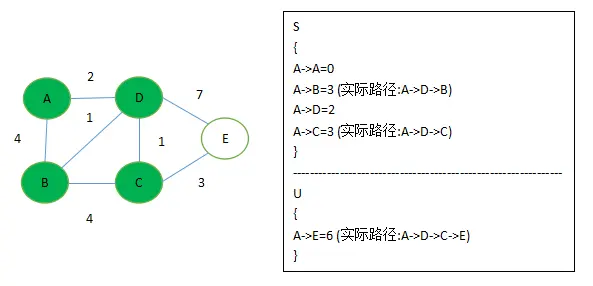
-
算法结束
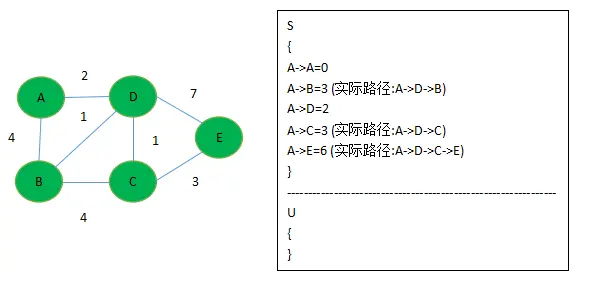
code
City Greph
package graph;
import java.util.*;
class City {
private Map<String, List<Node>> adj = new HashMap<>();
void addNode(String node) {
adj.putIfAbsent(node, new ArrayList<>());
}
void addEdge(String node1, String node2, int weight) {
adj.get(node1).add(new Node(node2, weight));
adj.get(node2).add(new Node(node1, weight));
}
/**
* 使用 Dijkstra 算法求解。Dijkstra 算法是一种常用的求解最短路径的算法,它的核心思想是贪心,每次选择离源点最近的节点,并使用该节点来更新其他节点的最短距离。
*
* 算法步骤如下:
*
* 1.创建一个集合 S,初始时将源节点加入。
* 2.创建一个距离映射 dist,用于存储源点到各节点的最短路径权重和,初始时将所有节点的距离设为无穷大,源节点距离设为 0。
* 3.从距离源点最近的节点开始,将该节点加入集合 S,并使用该节点来更新其他节点到源点的距离。
* 具体做法是:对该节点的每个邻居节点,计算经过该节点到达该邻居节点的距离,如果这个距离比之前记录的距离更短,就更新 dist 中存储的距离值。
* 4.重复第3步,直到目标节点被加入集合 S 为止。此时 dist 中存储的就是源点到各节点的最短距离。
* 5.为了获得最短路径的节点序列,我们需要从目标节点开始,不断找出前驱节点,直到回到源节点为止。
* @param source
* @param dest
* @return
*/
List<String> shortestPath(String source, String dest) {
// 创建存储顶点到起点的距离的映射
Map<String, Integer> dist = new HashMap<>();
// 创建存储顶点的前一个顶点的映射,用于最终构建最短路径
Map<String, String> prev = new HashMap<>();
// 创建存储已访问顶点的集合
Set<String> visited = new HashSet<>();
// 创建优先队列,用于按照顶点到起点的距离进行排序
PriorityQueue<Node> pq = new PriorityQueue<>((a, b) -> a.weight - b.weight);
// 初始化距离映射,将所有顶点的距离初始化为无穷大
for (String node : adj.keySet()) {
dist.put(node, Integer.MAX_VALUE);
}
// 将起点到自身的距离初始化为0
dist.put(source, 0);
// 将起点加入优先队列
pq.offer(new Node(source, 0));
// Dijkstra算法的核心部分
while (!pq.isEmpty()) {
// 从优先队列中取出当前距离起点最近的顶点
Node curr = pq.poll();
String node = curr.node;
int weight = curr.weight;
// 如果当前顶点已访问过,则跳过
if (visited.contains(node)) continue;
// 将当前顶点标记为已访问
visited.add(node);
// 遍历当前顶点的邻居节点
for (Node neighbor : adj.get(node)) {
String nextNode = neighbor.node;
int newWeight = weight + neighbor.weight;
// 如果通过当前顶点到达邻居节点的路径比之前计算的距离短,则更新距离映射和前一个顶点映射
if (newWeight < dist.get(nextNode)) {
dist.put(nextNode, newWeight);
prev.put(nextNode, node);
// 将邻居节点加入优先队列,以便后续继续迭代
pq.offer(new Node(nextNode, newWeight));
}
}
}
// 构建最短路径
List<String> path = new ArrayList<>();
String curr = dest;
// 从目标节点开始,沿着前一个顶点映射逆向遍历,直到回到起点
while (prev.containsKey(curr)) {
path.add(0, curr);
curr = prev.get(curr);
}
// 将起点加入到路径中
path.add(0, source);
return path;
}
private static class Node {
String node;
int weight;
Node(String n, int w) { node = n; weight = w; }
}
}
Main
public static void main(String[] args) {
City c = new City();
c.addNode("北京");
c.addNode("天津");
c.addNode("济南");
c.addNode("南京");
c.addNode("郑州");
c.addEdge("北京", "天津", 1);
c.addEdge("北京", "郑州", 1);
c.addEdge("天津", "济南", 1);
c.addEdge("济南", "南京", 1);
c.addEdge("南京", "郑州", 1);
List<String> path = c.shortestPath("南京", "北京");
System.out.println("从南京到北京的最短路径: " + path);
}
输出:
从南京到北京的最短路径: [南京, 郑州, 北京]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号