什么是算法程序?
算法程序通常指的是执行特定算法的计算机程序。要深入理解这个概念,我们可以将其分解为“算法”和“程序”两部分,并探究它们的基本含义。
简而言之:对特定问题求解过程的描述。
算法 (Algorithm):
定义:算法是解决问题的明确步骤序列,它是独立于任何编程语言的,可以用伪代码、流程图或者简单的自然语言来描述。
特点:
- 有穷性:算法在执行有限步骤之后会自动结束。
- 确定性:算法的每一个步骤都有明确的定义,不会产生二义性。
- 输入:算法有0个或多个输入。
- 输出:算法有一个或多个输出,是算法处理输入后的结果。
- 可行性:算法的每一步都必须足够基础,可以通过已有的基本运算步骤实现。
程序 (Program):
定义:程序是算法用某种编程语言的具体实现,它是指令的集合,计算机可以直接解释或编译后执行这些指令。
特点:
- 语言相关:程序必须用一种计算机可以理解的语言编写,如Python、C++、Java等。
- 可执行:程序可以在计算机上运行,对输入数据进行处理,输出结果。
- 交互性:程序可以与用户或其他系统交互,响应输入并提供相应的输出。
怎么检验算法程序的好坏?
衡量算法效率的标准是时间,而衡量时间的标准则是算法需要的步骤数。
为什么说衡量时间的标准是程序的步骤数?
同样的程序在不同的机器上运行,如果机器间硬件差异大,那么得到的时间肯定是不一样的。
而不管什么机器,他们所需要执行的步骤数一定是一致的,所以使用步骤数作为衡量的标准。
简而言之:衡量算法效率的唯一指标就是算法需要的步骤数。
怎么得到算法需要的步骤数?
使用大O表示法。在计算机科学中,它在分析算法复杂性的方面非常有用。
大O表示法定义:
在计算机科学里,大O 表示法用来表示一个算法的上界。用输入函数的大小来表示算法的最大运行时间。
大O表示法
什么是大O表示法?
result = O(int n); 就类似一个函数,你输入数字进去,会得到一个数字结果。
下图是一个很好的记忆辅助工具图,展示了算法的相对速度。(如果有的选,就选更快的算法!)
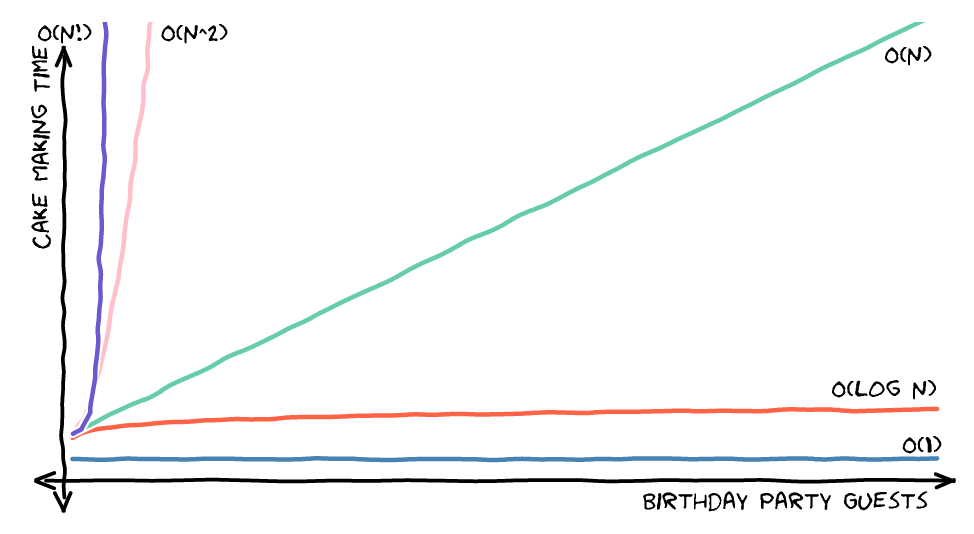
希望下面的生日蛋糕能让大 O 表示法更好理解。
O(1) - 常数时间
对于常数时间,举例:不管多少人参加生日聚会,都只需要做一个蛋糕。因此制作蛋糕的时间是一个常量。
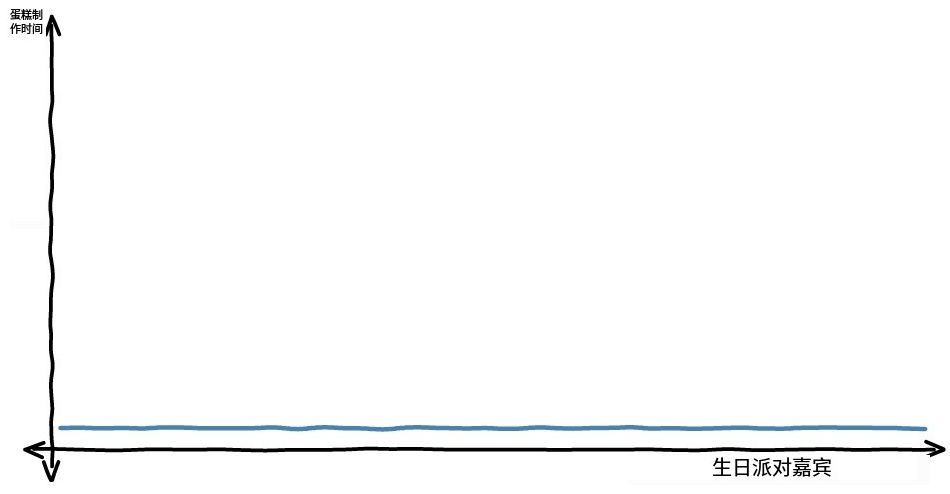
O(1):常数复杂度。表示无论输入规模如何增长,算法的执行时间都保持不变。
O(log n) - 对数时间
一个 O(log n) 操作的例子是有序数组的二分查找。
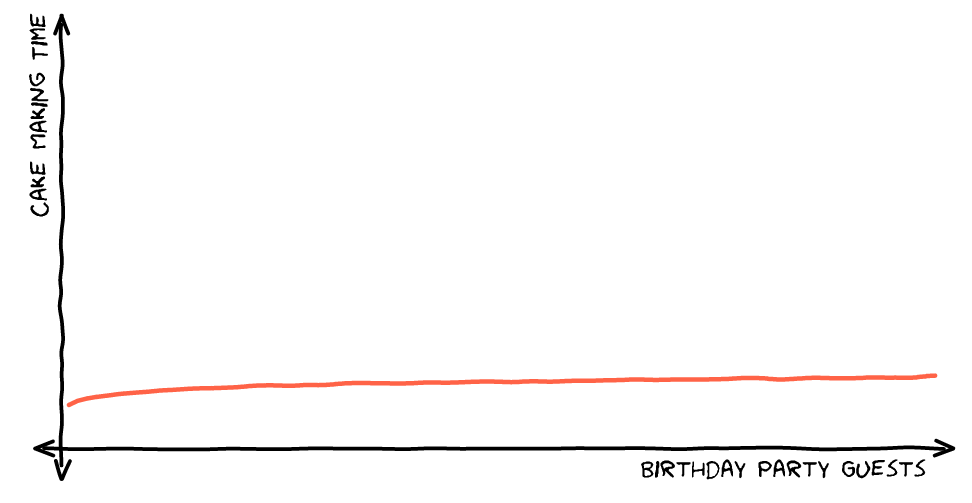
O(log n):对数复杂度。表示算法的执行时间与输入规模的对数成正比。
在数据结构中,操作的时间复杂度为 ( \log N ) 通常比 ( N ) 更高效。这里是为什么以及如何计算:
1. 什么是 ( log N )

2. 为什么 ( log N ) 比 ( N ) 高效 ?

3. 应用场景
- 二分查找:在一个排序好的数组中查找一个元素,时间复杂度为 $ ( O(\log N) )$,因为每次查找可以将搜索空间减少一半。
- 平衡树:如 AVL 树、红黑树等,基本操作(插入、删除、查找)都有 $ ( O(\log N) ) $ 的复杂度。
4. 计算 ( log N ) 的简单方法
可以通过反复将 ( N ) 除以 2 来估算 \(( log_2 N )\) 的值,直到结果为 1:
N = 16
16 / 2 = 8
8 / 2 = 4
4 / 2 = 2
2 / 2 = 1
这里操作了 4 次,所以 $ ( \log_2 16 = 4 ) $。
5. Log N 的底数是什么?

总之,在大 O 表示法中,底数是可以忽略的,主要关注的是增长的速度。
总结
$ ( \log N ) $ 的效率来源于其缓慢的增长速度,使得在处理大规模数据时显得更加高效。
O(n) - 线性时间
一个 O(n) 操作的例子是用最粗暴的方式在数组里遍历找到指定元素。在 10 个元素的数组里,最坏情况下需要找十次才能找到指定元素。在 100 万个元素的数组里,可能需要找 100 万次。
O(n):线性复杂度。表示算法的执行时间与输入规模成线性关系。
O(n^2) - 二次时间
对于二次时间,举例来说,每个参会者都有属于自己的蛋糕,另外,每个蛋糕上的都会有所有人在上面签名。

O(n^2):二次复杂度。表示算法的执行时间与输入规模的平方成正比。
O(n!) - 阶乘时间
如果我们只有一个乐高积木,很显然,我们只需要完成一次任务。如果有两个乐高积木,我们有两种选择的可能,:
- 可以是“先叠塔后建桥”
- 或者“先建桥后叠塔”; (所以我们得完成2次任务)
如果有三个乐高积木,可能性就更多了:
- “先叠塔、再建桥、最后造房子”
- 或者“先造房子、再叠塔、最后建桥”
- ……一共有6种可能的顺序。
我们可以看到,每增加一个乐高积木,可能的任务完成顺序会急剧增加。
如果我们有4个乐高积木,可能的顺序就有24种(也就是4的阶乘,即4!);如果有5个,就有120种(5!);以此类推。
现在,我们用大O表示法来描述这个情况。我们说,如果游戏的规则要求我们探索每一种可能的顺序,那么这个游戏的难度(或者说我们完成任务所需要的时间)是“阶乘时间”的,用大O表示法就是O(n!),其中n是乐高积木的数量。这意味着,乐高积木数量的一个小小增加会让游戏变得极其困难,因为可能的顺序数量增加得非常快。

O(n!)表示阶乘时间复杂度,其中n是输入规模。阶乘时间复杂度表示算法的执行时间与输入规模的阶乘成正比。
具体来说,如果一个算法的时间复杂度为O(n!),则意味着随着输入规模n的增加,算法的执行时间将按照输入规模的阶乘增长。这种复杂度通常非常高,意味着算法的执行时间会非常快速地增长,因此阶乘时间复杂度的算法通常不适用于大规模数据的情况。
举例来说,如果一个算法的时间复杂度是O(n!),那么当n=3时,执行时间可能是1秒;当n=4时,执行时间可能是24秒;当n=5时,执行时间可能是120秒,以此类推。因此,随着输入规模的增加,执行时间会非常快速地增长。
阶乘时间的例子在现实中比较少见,因为随着n的增长,时间复杂度会变得非常高,这样的算法通常不适用于大量数据的处理。
常见的阶乘时间算法包括:
- 解决旅行推销员问题(寻找最短可能路径访问一系列城市并返回出发点)的暴力搜索算法。
- 旅行商问题。
程序优化
-
确定代码效率是优化的第一步;
如果连代码运行速度都不知道,那又怎么能知道怎么修改让他变得更快呢?
参考:《秒懂算法:用常识解读数据结构》第7章 -
一般认为复杂度为 O(N^2)的算法是比较慢的。如果你的算法也属于此类,可以停下来思考一下有没有优化方法。
当然 O(N^2)的算法对于特定问题来说,可能就是最优解了。
Reference
图解大 O 表示法
https://www.freecodecamp.org/chinese/news/big-o-notation/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号