线性代数是数学的一个分支,研究向量空间和线性映射的性质和结构。它在许多领域中都有广泛的应用,包括物理学、工程学、计算机科学、经济学等。
线性代数解决以下几类问题
- 线性方程组求解:线性代数提供了求解线性方程组的方法和技巧。线性方程组是一组关于未知量的线性方程,例如:
2x + 3y - z = 1
4x - y + 2z = 3
x + 2y + z = 4
通过线性代数的技术,可以求解未知量x、y和z的值,从而找到满足这些方程的解。
-
向量空间和线性变换:线性代数研究向量空间的性质和结构,这对于理解几何空间、物理学中的向量量表达、图像处理等领域非常重要。线性变换是一种保持向量相加和标量乘法的性质的映射关系,它可以用矩阵来表示。线性代数提供了分析和求解线性变换的工具,例如矩阵运算、特征值和特征向量等概念。
-
最小二乘法:线性代数在回归分析和数据拟合中有重要应用。最小二乘法是一种通过最小化观测值与模型预测值之间的差异来拟合数据的方法。线性代数提供了求解最小二乘问题的技术,例如通过矩阵求导和矩阵运算来找到最优解。
-
特征值和特征向量:线性代数中的特征值和特征向量在很多应用中都有重要作用。特征值和特征向量描述了线性变换对于某些向量的影响,它们在图像处理、信号处理、网络分析等领域中被广泛应用。线性代数提供了计算特征值和特征向量的方法,例如特征值分解和奇异值分解等。
把上面不清楚的名词,都解释一遍。
特征值和特征向量是什么?
在线性代数中,特征值和特征向量是描述线性变换对向量的影响的重要概念。
假设我们有一个线性变换,表示为一个矩阵A,和一个非零向量v。如果存在一个标量λ使得下面的等式成立:
A v = λ v
其中,λ是标量,v是非零向量,那么我们称λ为特征值,v为对应于特征值λ的特征向量。
特征值描述了线性变换在特征向量方向上的缩放效果。当我们将特征向量v应用于线性变换A时,结果只是将v进行缩放,缩放因子就是特征值λ。特征向量则表示这个被缩放的方向。
让我举一个简单的示例来说明。
假设我们有一个二维空间中的线性变换,表示为矩阵:
A = [2 1]
[1 2]
我们想找到它的特征值和特征向量。
首先,我们需要解方程(A - λI)v = 0,其中I是单位矩阵,v是特征向量,λ是特征值。我们要找到使得该方程成立的λ和v。
将矩阵A减去λ乘以单位矩阵I并代入方程,得到:
[2-λ 1]
[1 2-λ] [v1] = [0]
我们需要找到非零解v=[v1 v2],使得上述等式成立。这等效于求解以下方程组:
(2-λ)v1 + v2 = 0
v1 + (2-λ)v2 = 0
通过解这个方程组,我们可以得到特征值和特征向量。
解方程组后,我们发现有两个解:λ1 = 1,λ2 = 3。
对于λ1 = 1,我们可以找到一个对应的特征向量v1 = [1 -1]。
对于λ2 = 3,我们可以找到一个对应的特征向量v2 = [1 1]。
所以,矩阵A的特征值是λ1 = 1和λ2 = 3,对应的特征向量分别是v1 = [1 -1]和v2 = [1 1]。
这意味着在线性变换A中,特征值1对应的特征向量[1 -1]表示在这个方向上变换只进行了缩放,特征值为3对应的特征向量[1 1]也表示在这个方向上变换只进行了缩放,只是缩放的程度不同。
特征值和特征向量在很多应用中都有重要作用,它们提供了对线性变换的关键理解。
什么是非零向量?
非零向量v指的是一个向量,其元素不全为零。换句话说,至少存在一个元素在向量中具有非零值。
在线性代数中,我们通常将零向量表示为一个元素全为零的向量,如[0 0]或[0 0 0]等。而非零向量则是除了零向量之外的任何向量。
例如,向量v = [1 2 0]是一个非零向量,因为它包含非零元素1和2,而且不是全为零的向量。
特征向量的定义要求它是一个非零向量,因为特征向量的目的是描述线性变换在某个方向上的影响,而只有非零向量才有方向。如果特征向量为零向量,那么线性变换对应的特征值就没有实际的几何意义。因此,在特征值和特征向量的定义中,通常要求特征向量是非零向量。
一些思考
感觉是线性代数就是研究一些数据群的特征的学问,比如分解质数是研究单个质数,这里的线性代数是研究一群的数,对他们统一做一些运算,然后得出一个运算结果。通过这些关系发现数据群的特征和性质。
应用示例
假设你是一位学生,你参加了一个关于学生体能测试的调查。你记录了每个学生的体重、身高和跑步成绩。现在你想通过这些数据来分析体重和身高对跑步成绩的影响。
首先,你可以将每个学生的体重、身高和跑步成绩表示为向量。假设你有5个学生的数据,你可以将它们表示为以下向量:
体重向量 W = [60, 65, 70, 55, 75](单位:千克)
身高向量 H = [160, 165, 170, 155, 180](单位:厘米)
跑步成绩向量 S = [7.5, 8.2, 8.5, 7.1, 9.0](单位:分钟)
现在,你想探索体重和身高对跑步成绩的影响,你可以使用线性代数中的向量运算来分析如下关系:
-
例如,你可以计算身高和跑步成绩之间的相关性。通过计算身高向量 H 和跑步成绩向量 S 的点积(内积),你可以得到一个标量值,表示身高和跑步成绩之间的相似程度。如果点积的值接近于1,说明身高和跑步成绩正相关;如果接近于-1,说明身高和跑步成绩负相关;如果接近于0,说明身高和跑步成绩之间几乎没有关系。
-
另外,你还可以使用矩阵乘法来进行线性回归分析,以预测跑步成绩。你可以将体重向量 W 和身高向量 H 组合成一个特征矩阵 X,矩阵的每一列代表一个特征,每一行代表一个样本。然后,你可以将特征矩阵 X 与跑步成绩向量 S 进行矩阵乘法,得到一个预测值向量 Y,其中每个元素表示对应样本的预测跑步成绩。这样,你就可以使用线性回归模型来预测一个学生的跑步成绩,基于其体重和身高的特征。
-
直观地看到体重和身高与跑步成绩之间是否存在某种趋势:
下面绘制两个散点图:一个显示体重与跑步成绩的关系,另一个显示身高与跑步成绩的关系。通过这些散点图,你可以直观地看到体重和身高与跑步成绩之间是否存在某种趋势或关系。
图1
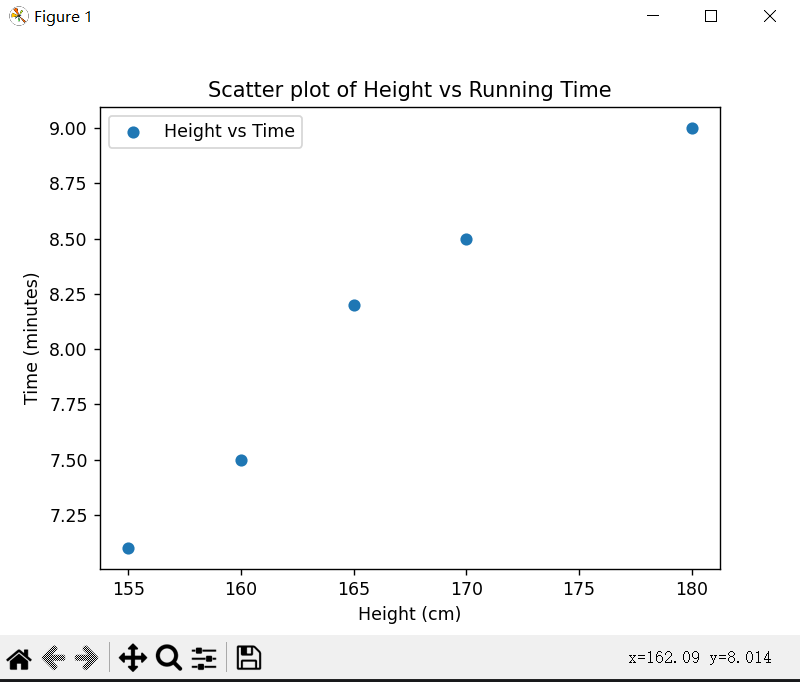
图2
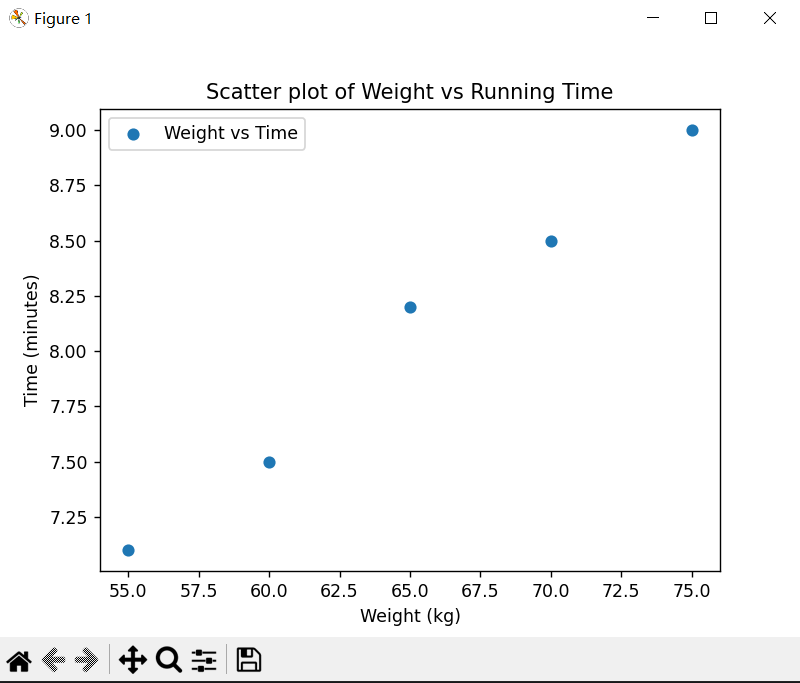
python Code:
import matplotlib.pyplot as plt
# 数据
weights = [60, 65, 70, 55, 75] # 体重向量 W
heights = [160, 165, 170, 155, 180] # 身高向量 H
times = [7.5, 8.2, 8.5, 7.1, 9.0] # 跑步成绩向量 S
# 绘制体重与跑步成绩的散点图
plt.scatter(weights, times, label='Weight vs Time')
plt.xlabel('Weight (kg)')
plt.ylabel('Time (minutes)')
plt.title('Scatter plot of Weight vs Running Time')
plt.legend()
plt.show()
# 绘制身高与跑步成绩的散点图
plt.scatter(heights, times, label='Height vs Time')
plt.xlabel('Height (cm)')
plt.ylabel('Time (minutes)')
plt.title('Scatter plot of Height vs Running Time')
plt.legend()
plt.show()
计算步骤:
TODO


