向量的乘法工具有两种主要类型:
- 点乘(内积)
- 叉乘(外积)
点乘
点乘的核心目标:
点乘的结果就是求两个向量之间的夹角关系。
点乘又叫向量的内积、数量积,是一个向量和它在另一个向量上的投影的长度的乘积;是标量。
点乘反映着两个向量的“相似度”,两个向量越“相似”,它们的点乘越大。反之...

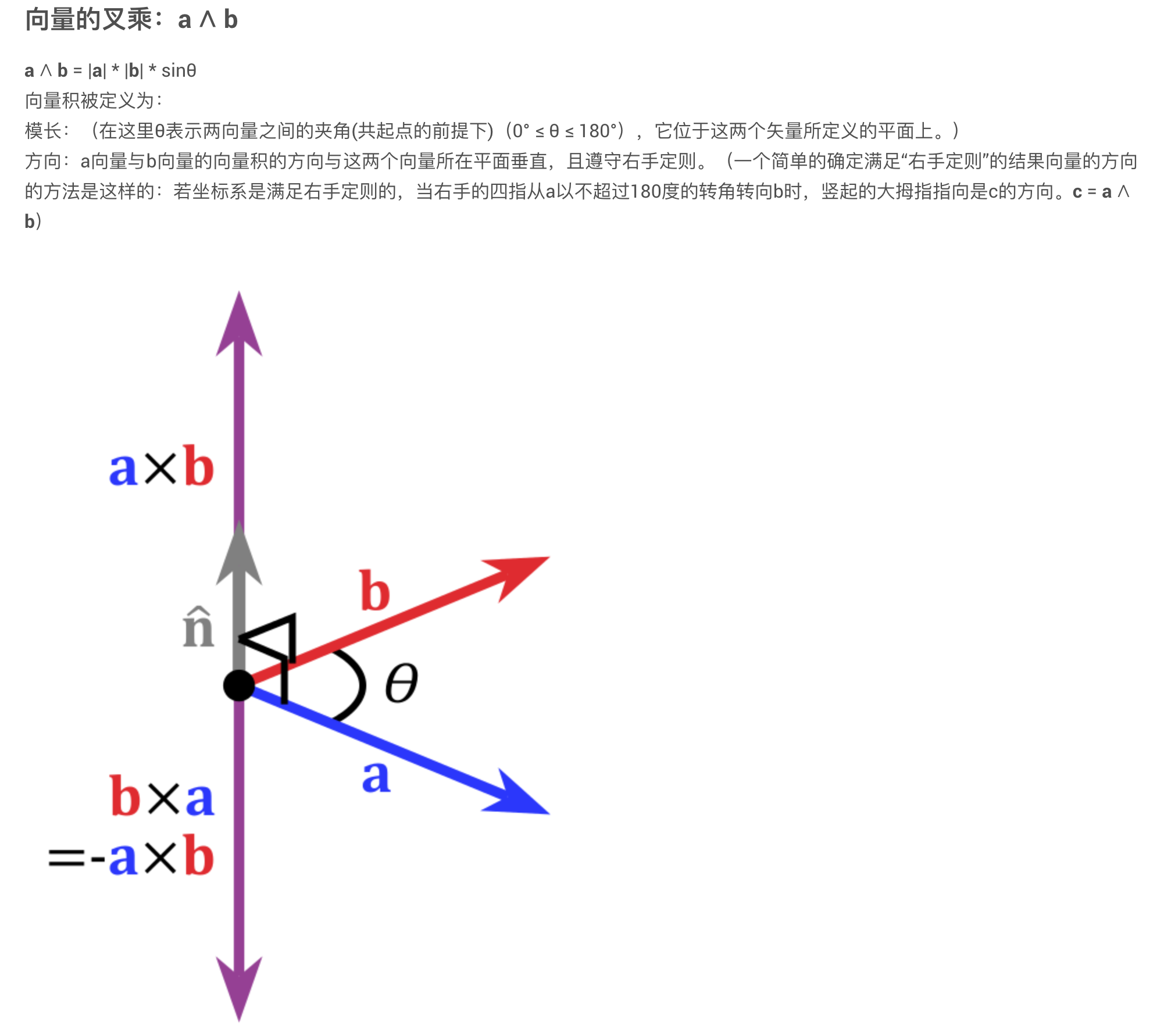
叉乘
叉乘的核心目标:
叉乘的结果是两个向量的长度表示了两个原始向量之间的夹角的正弦值的大小。
叉乘所得结果是两个垂直于两个向量的直线,大小为两个向量所在平面所组成的平行四边形的面积。

这些角度值有什么用?
这写角度值在很多领域都有应用,尤其是在物理学、工程学和计算机图形学等领域。
-
物理学:在物理学中,向量的夹角关系经常用于描述力、速度、加速度等物理量之间的关系。例如,在力学中,两个力的夹角可以告诉我们它们之间的相对方向,以及对物体施加的结果。
-
工程学:在工程学中,向量的夹角关系可以用来分析力学系统、电路等。例如,在机械工程中,两个向量的夹角可以用来计算受力构件的应力和应变,以及分析构件的稳定性。
-
计算机图形学:在计算机图形学中,向量的夹角关系用于表示光照、阴影等效果。例如,在三维渲染中,两个向量的夹角可以用来计算光源和表面法线之间的关系,从而确定光照的强度和颜色。
-
机器学习和数据分析:在机器学习和数据分析中,夹角关系可以用于特征之间的相似性和相关性分析。例如,在文本分类中,可以使用向量的夹角来度量两篇文章之间的相似性。
总的来说,向量的夹角关系可以帮助我们理解和分析复杂的问题,并且在解决实际问题时提供了重要的参考和指导。


