How to understand matrix and vector（Primary）

What is Matrix?

What is Vector ?

在数学里，用有序的数字列表来描述的对象被称为向量（vector），有一个领域专门研究它，称为线性代数。例如，一辆二手车可能对应的是一个四维向量，也就是一个包含四个数的元组。

例如：
(2015, 41429, 22.27, 16980) 这些数分别代表出厂日期、里程数、停留天数、价格。

What is Eigenvector and Eigenvalue？

任何只被矩阵缩放而不被旋转的矢量被称为该矩阵的特征向量（Eigenvector），而向量被缩放的程度称为特征值（Eigenvalue）。

What is Linear algebra?

不同的输入矢量会被缩放和旋转得到不同的结果。然而，这些变换都是线性的，也就是说，任何与输入矢量在同一条线上的矢量都会被映射到与相应输出矢量在同一条线上。

Example ———— 解方程

学到的矩阵的第一个应用是如何帮助我们解决方程组。
question:

\[3x - 2y = 1 \\ -x + 4y = 3 \]

系数可以放入一个矩阵，变量放入另一个，输出放在等式右边;

\[\begin{pmatrix} 3 & -2 \\ -1 & 4 \end{pmatrix} \binom{x}{y} = \binom{1}{3} \]

然后怎么求出X,Y？

逆矩阵

从正向来看，

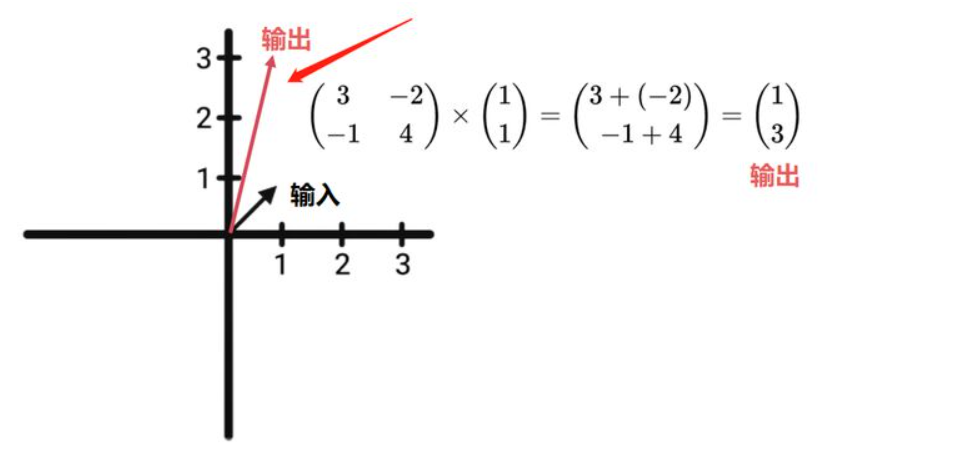
矩阵 * （1,1） = （1,3），这个问题是要求我们找出这个矩阵将哪个输入矢量映射到（1,3）。

但是问题是我们怎么知道矩阵将哪个输入矢量映射到这个输出？ 我们只需要做之前相同的变换，反向进行，即可找到答案（1,1）。

求解逆矩阵：

\[A_{}^{-1} \binom{1}{3} = \binom{1}{1} \]

TODO

求多变量问题——就要想到矩阵

矩阵的常用应用，当方程组变得更复杂时，我们只需要扩展矩阵，就可以分析具有任意多个变量的系统。

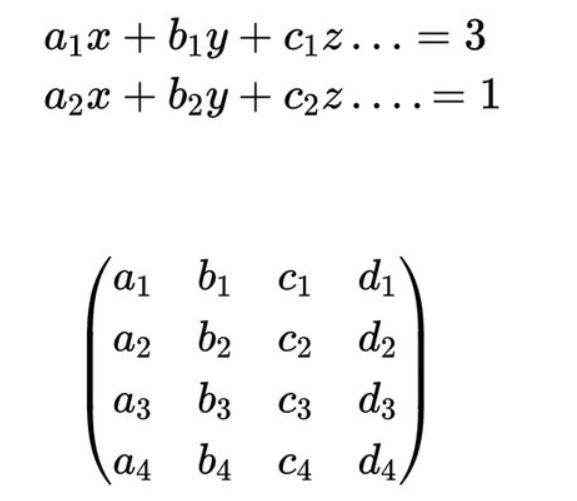
图片的旋转（图片操作）

Reference：https://blog.csdn.net/yuezhilanyi/article/details/117423755

输入一个矩阵，求出一些边界、和偏移量之后，
图像的旋转的操作是，使用最基础直接的方式对图像旋转，即用一个二重循环，对图像上的每一个点，经由矩阵乘法获取其新坐标，并将原图的像素值复制过去。

# 构建一个空数组，用于放置旋转后的图像
rotated_img = np.empty((new_h + 0, new_w + 0, 3), dtype='uint8')
# 迭代每一行
for i in range(h):
	# 迭代每一列
    for j in range(w):
    	# 计算新坐标：矩阵乘之后，减去偏移量
        new_coord = np.dot(rotation_matrix, [i, j, 1]).astype(np.int16)[:2] - min_value
        # 赋值
        # 这里注意要用`tuple(new_coord)`而不是数组或者列表，否则是对选定得两行赋值
        rotated_img[tuple(new_coord)] = img_arr[i, j]

求电流和电压

矩阵在电路和电子领域的应用之所以重要，是因为这些可以用线性方程表示，其中所有电压和电流都是未知变量。
当电路变得复杂时，我们只需要让计算机找到一个逆矩阵，就能得到我们需要的电流和电压。

Reference

posted on 2023-06-26 15:12  Mysticbinary  阅读(33)  评论(0)  编辑  收藏  举报