python画连续变量柱状图

弗里德曼-迪亚科尼斯规则

在统计学中，Freedman-Diaconis规则用于确定直方图中的条柱宽度, 它以David A.Freedman和Persi Diaconis的名字命名。该规则定义：

\[条柱宽度 = 2 \times \frac{IQR}{\sqrt[3]{n}} \]

其中，IQR是四分位距，n是观测样本数目。

import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt

plt.rcParams["font.sans-serif"] = ["SimHei"]

# 1. 导入数据
file_path = r"../../机器学习数据/data_train.csv"
df = pd.read_csv(file_path, encoding='gbk')

# 2. 查看数据
# print(df.head())
# print(df.columns)
# print(df.info)
# print(df.isnull().sum())  # 检查空值
std = df["房价"].describe()


def freedman_diaconis(x):
    """
    :param x: 输入数据
    :return num_bin: 条柱数目
    """
    static = x.describe()
    IQR = static["75%"] - static["25%"]
    bin_width = (2 * IQR) / np.power(x.shape[0], 1 / 3)
    x_max, x_min = static["max"], static["min"]
    num_bin = int(((x_max - x_min) / bin_width) + 1)
    return num_bin


bins = freedman_diaconis(df["房价"])  # 箱子数目

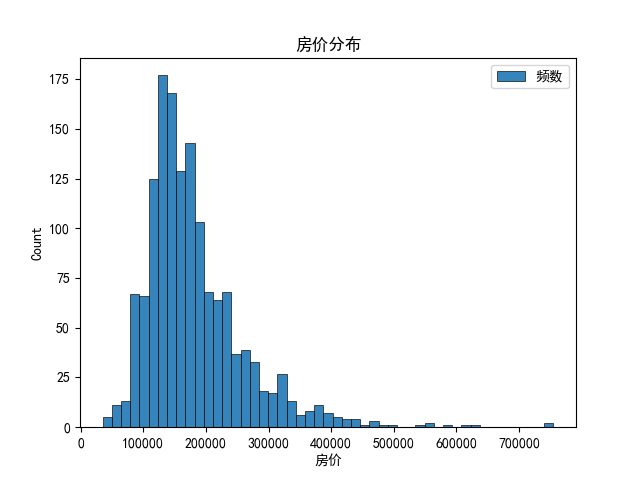
plt.figure()
plt.hist(df["房价"], bins=bins, edgecolor="black", linewidth=0.5, alpha=0.9)
plt.title("房价分布")
plt.xlabel("房价")
plt.ylabel("Count")
plt.legend({"频数"})
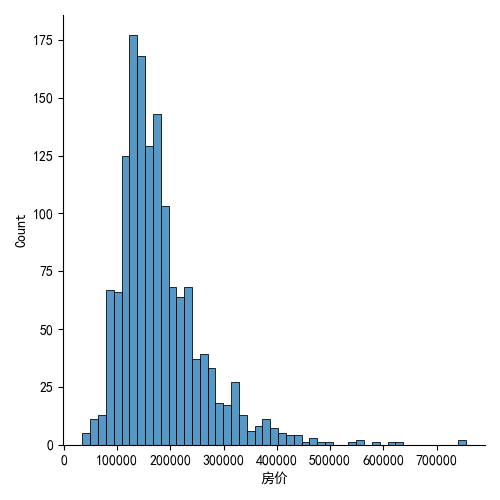
sns.displot(df["房价"])
plt.show()

模仿：

sns.displot():