改进的蝙蝠算法-ELBA

1. 简介

Lucas等人提出了一种改进的蝙蝠算法，称为增强Levy飞行蝙蝠算法-ELBA。从计算的角度来看，ELBA的主要创新在于:(1)引入了特定的数学表达式，增强了种群多样性；(2)采用基于Levy飞行的数学表达式进行有效的局部搜索；(3)选择新的参数控制方程。该算法很好的平衡了局部开发和全局探索之间的平衡。仿真结果表明，ELBA算法在有效性、鲁棒性、稳定性、收敛速度和仿真时间等方面都具有很强的竞争力。

2. 核心公式

\[x_{i}^{t+1} = x_{i}^{t} + rand(x_{b1}^{t}-x_{b2}^{t}) + rand(x_{b3}^{t}-*x_{b4}^{t}) \tag{15} \]

\[x_{i}^{t+1} = x_{i}^{t} + (x^{*} - x_{i})f_{i} \tag{16} \]

\[x_{i}^{t+1} = x_{i}^{t} + 0.01s(x^{*} - x_{i}) \tag{19} \]

\[r_{i} = (r_0 - r_{\infty})(\frac{t-t_{max}}{1-t_{max}}) + r_{\infty} \tag{20} \]

\[A_{i} = (A_0 - A_{\infty})(\frac{t-t_{max}}{1-t_{max}}) + A_{\infty} \tag{21}\\ \]

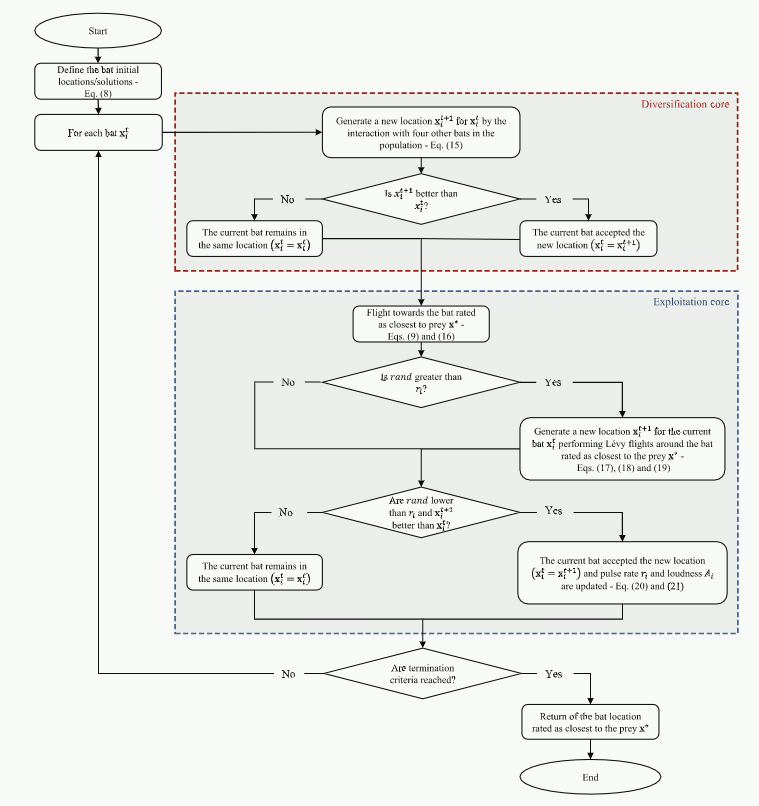
2. 算法流程图

3. 实验-matlab

% =========================================================================
% Title: ELBA
% Author: Lee WenTsao
% Time: 2022-04-16
% Reference:Parameter extraction of photovoltaic models using an enhanced
%           Levy flight bat algorithm
% =========================================================================
clc;
clear;
close all;

%% 添加路径
addpath("..\优化函数\");

% run_time = 30;
% best_fmin = zeros(run_time,1);
% for run=1:run_time 
%     Option = 2;
%     [Fun, bound] = Optimizer(Option);

    %% 问题参数定义
    n = 50;  % 种群规模
    d = 3;   % 维度
    
%     Lb = bound(1)*ones(1,d);  % 种群下界
%     Ub = bound(2)*ones(1,d);  % 种群上界
    ub = [2, 1.3, 15];     % 上界
    lb = [0.05, 0.25, 2];  % 下界

    Fun = @ fobj;
    
    
    %% 蝙蝠算法参数定义
    A_min = 1;
    A_max = 0;
    
    r_min = 0;
    r_max = 1;
    
    
    Freq_min = 0;     % 蝙蝠发射频率的下界
    Freq_max = 5;     % 蝙蝠发射频率的上界
    
    t_max = 1000;     % 最大迭代次数
    
    fmin = inf;
    best = zeros(1, n);
    
    %% 初始化
    v = zeros(n, d);
    Fitness = zeros(n, 1);
    Sol = zeros(n, d);
    for i=1:n  
        for j=1:d
            Sol(i, j) = rand*(ub(j) - lb(j)) + lb(j); % 初始化个体
        end
%         Sol(i, :) = Lb + (Ub - Lb).*rand(1, d);  % 随机初始化种群
        Fitness(i) = Fun(Sol(i, :));             % 评估
        
        if Fitness(i)<fmin
           best = Sol(i, :);
           fmin = Fitness(i);
        end
    end
    S = Sol;
    
    best_scores = [fmin];
    for iter=1:t_max
        r = (r_min-r_max)*(iter-t_max)/(1-t_max) + r_max;
        A = (A_min-A_max)*(iter-t_max)/(1-t_max) + A_max;
        for i=1:n
           %% Diversification core
            JK = randperm(n);
            S(i,:) = Sol(i, :) + rand*(Sol(JK(1),:) - Sol(JK(2),:))+ rand*(Sol(JK(3),:) - Sol(JK(4),:));
            newFun = Fun(S(i,:));
            if newFun<Fitness(i)
                Sol(i, :) = S(i,:);
                Fitness(i) = newFun;
            end
            
           %% Exploitation core
            Freq = Freq_min + (Freq_max - Freq_min)*rand;  % 频率更新公式 
            S(i,:) = Sol(i, :) + (best - Sol(i, :))*Freq;
            
            if rand>r 
                 L = Levy(d);
                 dS = L.*(Sol(i,:) - best);
                 S(i,:) = Sol(i,:) + dS;
            end
            S(i,:) = simplebounds(S(i,:),lb,ub);
            
            Fnew = Fun(S(i,:));
            if rand<r && Fnew<Fitness(i)
                Sol(i, :) = S(i,:);
                Fitness(i) = Fnew;
            end
    
            if Fnew<fmin
                best = S(i,:);
                fmin = Fnew;
            end
        end
        if ~mod(iter,50)
            disp(['Iter=', num2str(iter), '   ||  fmin=', num2str(fmin)]);
        end
%         best_scores = [best_scores,fmin];
    end
%     best_fmin(run) = fmin;
% end
% save('Ackley\ELBA_Ackley.mat',"best_fmin")
% 
% disp(["标准差：", num2str(std(best_fmin))]);
% disp(["最优值：", num2str(min(best_fmin))]);
% disp(["平均值：", num2str(mean(best_fmin))]);
% disp(["最差值：", num2str(max(best_fmin))]);
% csvwrite('E:\群智能算法路径规划\fmin.csv',best_scores)

%% matlab可视化
% figure
% xx = 1:50:1001;
% xxx = 0:50:1000;
% plot(xxx,log10(best_scores(xx)),'r','LineWidth',1.5);
% hold on;
% sz = 40;
% scatter(xxx(2:end-1),log10(best_scores(xx(2:end-1))),sz,'ro','filled');
% xlabel('$$Iteration$$','Interpreter','latex');
% ylabel('$$\log_{10} (fitness)$$','Interpreter','latex');
% title('Convergence curve')

% xticks(0:50:1000);
% xtickangle(45);

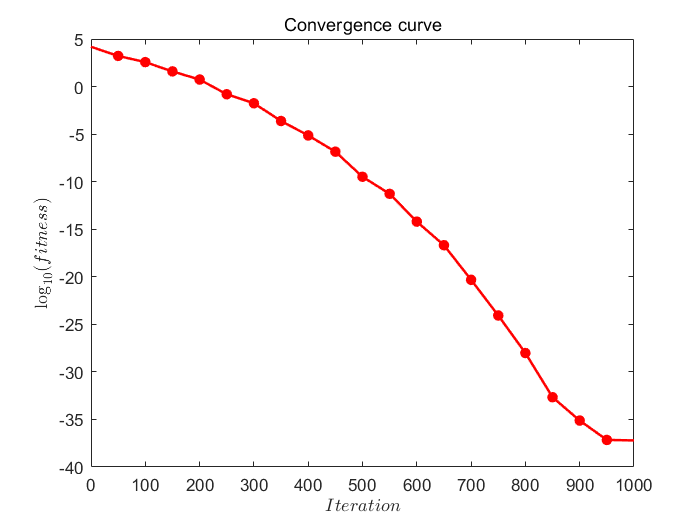
3. 实验效果

4. 参考文献

[1] Deotti L M P, Pereira J L R, da Silva Júnior I C. Parameter extraction of photovoltaic models using an enhanced Lévy flight bat algorithm[J]. Energy Conversion and Management, 2020, 221: 113114.