拉丁超立方体初始化种群(附Matlab代码)

拉丁超立方体初始化种群

1.引言

群智能算法一般以随机方式产生初始化种群的位置，但是这种方式可能导致种群内个体分布不均匀。拉丁超立方体抽样方法产生的初始种群位置，可以保证全空间填充和抽样非重叠，从而使种群分布均匀。

2.LHS抽样过程

step1: 确定抽样规模$H$
step2: 将每维变量$x^i$的定义域区间$[x_l^i,x_u^i]$划分成$H$个相等的小区间：

$$x_l^i=x_0^i<x_1^i<x_2^i<....<x_j^i<...<x_H^i=x_u^i$$

这样就将原来的一个超立方体划分成$H^n$个小超立方体。
step3:产生一个$H\times{n}$的矩阵$A$，$A$的每列都是数列${1,2,...,H}$的一个随机全排列。
step4:$A$的每行就对应一个被选中的小超立方体，在每个被选中的小超立方体内随机产生一个样本。

4.Matlab代码

% ======================================
%         拉丁超立方体初始化种群
% ======================================

% step1:清理运行环境
close all;
clear
clc

% step2:参数设置
n = 30; % 确定抽样规模
d = 2;  % 维数

% step3:划分小超立方体
lb = (0:n-1)./n;
ub = (1:n)./n;

% step4:产生一个H*n的全排列矩阵
A = zeros(n, d);
for i=1:d
    A(:,i) = randperm(n);
end

% step5:采样
H = zeros(n,d);
for i=1:n
    for j=1:d
        H(i,j) = unifrnd(lb(A(i,j)), ub(A(i,j)));
    end 
end

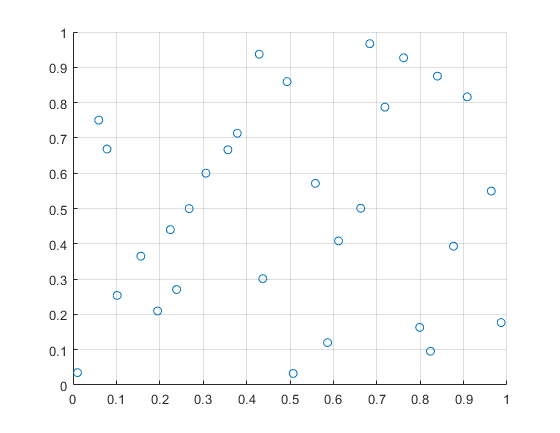
% step6:可视化
figure
scatter(H(:,1),H(:,2));
xlim([0, 1]);
ylim([0, 1]);
grid on;

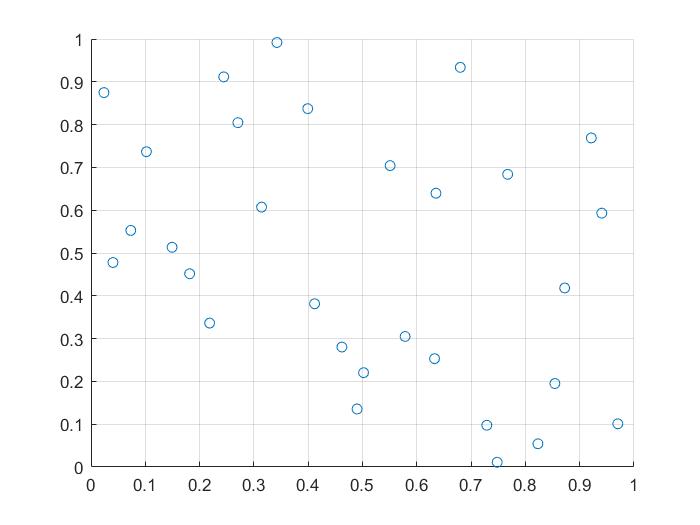
% 拉丁超立方体抽样函数
x = lhsdesign(30, 2);
% step6:可视化
figure
scatter(x(:,1),x(:,2));
xlim([0, 1]);
ylim([0, 1]);
grid on;