KMP算法

KMP算法是用来进行字符串匹配的算法。

核心概念

1、s[ ]是模式串，即比较长的字符串。

2、p[ ]是模板串，即比较短的字符串。用P去匹配S。

3、“非平凡前缀”：指除了最后一个字符以外，一个字符串的全部从头部字符到末尾字符的前一个的所有组合。

4、“非平凡后缀”：指除了第一个字符以外，一个字符串的全部从尾部字符到头部字符的后一个的所有组合。（后面会有例子，均简称为前/后缀）

5、“部分匹配值”：前缀和后缀的最长共有元素的长度。（称为最长公共子缀）

6、next[ ]是“部分匹配值表”，即next数组，它存储的是每一个下标对应的“部分匹配值”，是KMP算法的核心。next数组求法，就是

与自己进行匹配，从而递归算出，每一个下标对应的匹配值。

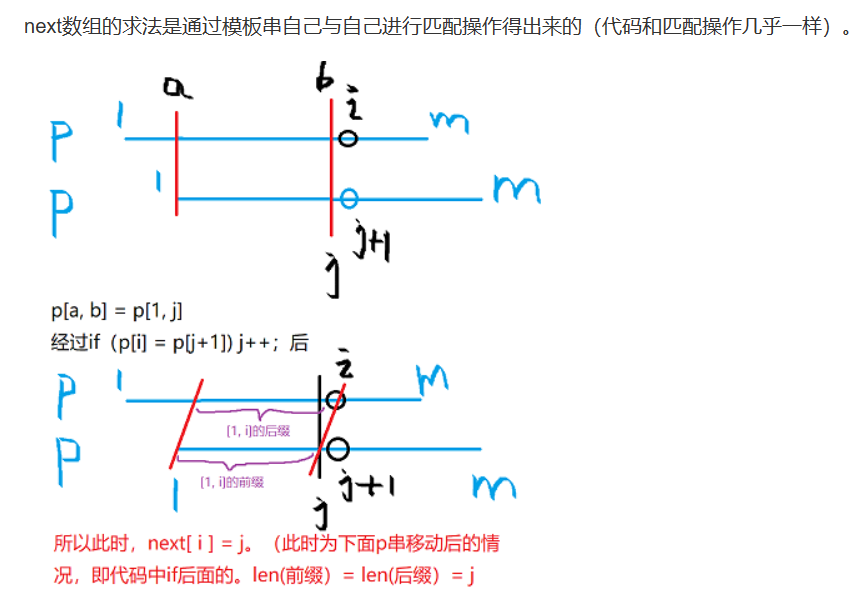
核心就是next[i]=j，因为长度就为j，所以next[i]匹配值就为j，并且next[j]就代表了1到j的长度，平移看就是1到等于j。

因为当前的p的下一个与s不匹配，所以p的指针j向前回退，回退到ne[j],此时为ne[6]，所以根据next匹配值表，知道了要回退到4的位置，因为C前面的前缀，即C前面的前4个与p的前4个一定相等，相等后，再用p的下一个去与s匹配，就不用重复匹配。如果不匹配继续往

后回退，直到退到开头为止。

核心思想：在每次失配时，不是把p串往后移一位，而是把p串往后移动至下一次可以和前面部分匹配的位置，这样就可以跳过大多数的失配步骤。而每次p串移动的步数就是通过查找next[ ]数组确定的。

下标要从0开始：

cin>> n >> p+1 >> m >>s+1; //下标从1开始，因为数组名代表了第一个元素的地址加1后，相当于下由0加到1。

#include <iostream>

const int N=100010,M = 1000010;
char s[M],p[N];
int ne[N];//用P去匹配S字符串
int n,m;  

using namespace std;

int main()
{
     cin >> n >> p + 1 >> m >> s + 1;
    //求kmp的next数组，p自己与自己匹配，从而预处理出来一个，ne[j]代表1到j与i-j+1到i的最长公共子缀，并且它的
   for(int i = 2,j = 0 ; i<=n ; i ++)                  //长度为j，并且因为数组从1开始的，所以j就是前缀的公共部分的
   {                                                   //末尾端点    
       while(j && p[i]!=p[j+1]) j=ne[j];   //一直向后退直到找到储存着最长子缀的信息，可以递归查询。
       if(p[i]==p[j+1]) j ++;
       ne[i]=j;  //当i与j+1相等时,前缀的末端点即（1,j)与i到i-j+1相匹配，从而延长了前缀长度。
   }             //所以1到i的长度就等于j了,并且把这个信息储存到ne数组中，并且随着循环的进行，从而得到
                 //了ne数组所存的值
    //kmp算法的匹配
   for(int i = 1,j=0;i <=m ; i ++)   //i是遍历目标字符串，j是模板字符串。n是模板字符串的长度
   {                                 //m是目标字符串的长度。ne[j]是最大公共子缀的末尾端点
       while(j && s[i]!=p[j+1]) j=ne[j];  //如果不是就用,ne[j]的位置信息值来替换掉j,从而使j之前的字符串都匹配
                                        //如果j到0说明都不匹配，就对i的下一个值进行匹配。
       if(s[i]==p[j+1]) j ++;             //如果当前匹配，再匹配j后面一个          
       if(j==n)                       //当模板字符串匹配完毕，则输出结果
       {
           cout<<i-n<<" ";          //输出起始位置，结束的时候，i是当前匹配的最后一个字符串的位置
           j=ne[j];               //上一个匹配成功后，再将预处理的前缀和后缀最长的公共子缀的末尾端点
       }                          //因为到该末尾端点包括端点之前的都匹配切长度等于n
   }                             //下一次就从这个端点往后进行匹配，匹配到s的端点。
    
    return 0;
}