字符串/规则匹配常用算法学习
前言:
也是前辈推荐的,一本好书《柔性字符串匹配》分享推荐一下,本文章内容部分是参考别的网站上的,如有侵权请及时联系我,汇总这个文章旨在扩展视野学习,能在实际工作提供一些思路
BF (Brute Force)暴力匹配算法
作为最简单、最暴力的字符串匹配算法,BF 算法的思想可以用一句话来概括,那就是,我们在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。
理论上的最坏情况时间复杂度是 O(n*m),但是,统计意义上,大部分情况下,算法执行效率要比这个高很多。
朴素字符串匹配算法思想简单,代码实现也非常简单。简单意味着不容易出错,如果有 bug 也容易暴露和修复。
1 /* 2 模式匹配之BF(Brute Force)暴力算法 3 */ 4 # include<iostream> 5 # include<string> 6 7 using namespace std; 8 9 /* 10 * 返回子串t在串s第一次出现的位置(从1开始) 11 */ 12 int patternMatch_BF(string s, string t) 13 { 14 int i = 1, j = 1; 15 while (i <=s.length()&& j <=t.length())//两个串都没扫描完 16 { 17 if (s[i-1] == t[j-1])//该位置上字符相等,就比较下一个字符 18 { 19 i++; 20 j++; 21 } 22 else 23 { 24 i = i - j + 2; //否则,i为上次扫描位置的下一位置 25 j = 1; //j从1开始 26 } 27 28 } 29 if (j > t.length()) 30 return (i - t.length()); 31 return -1; 32 } 33 34 int main() 35 { 36 string mstr = "sdsajdijaois"; 37 string sstr = jao; 38 39 int result = patternMatch_BF(mstr, sstr); 40 if (result==-1) 41 cout <<endl<< "匹配失败" << endl; 42 else 43 cout << endl<<"子串在主串中的位置为:" << result << endl; 44 return 0; 45 }
RK(Rabin-Karp) 算法
BF算法每次检查主串与子串是否匹配,需要依次比对每个字符,所以 BF 算法的时间复杂度就比较高,是 O(n*m)。
RK 算法的思路是这样的:
我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了。
模式串哈希值与每个子串哈希值之间的比较的时间复杂度是 O(1),总共需要比较 n-m+1 个子串的哈希值,所以,这部分的时间复杂度也是 O(n)。所以,RK 算法整体的时间复杂度就是 O(n)。
跟 BF 算法相比,效率提高了很多。不过这样的效率取决于哈希算法的设计方法,如果存在冲突的情况下,时间复杂度可能会退化。极端情况下,哈希算法大量冲突,时间复杂度就退化为 O(n*m)
1 class Solution 2 { 3 public: 4 int RK(const string& src,const string& dst) 5 { 6 int srcLength = src.size(); 7 int dstLength = dst.size(); 8 9 powValue = new int[dstLength-1]; 10 hashValue = new int[srcLength-dstLength+1]; 11 12 for(int i=0;i<dstLength;++i) 13 { 14 powValue[i]=1; 15 for(int j =i;j>0;--j) 16 { 17 powValue[i]*=26; 18 } 19 } 20 //计算子串的hash值 21 int dstHash = 0; 22 for(int j = 0;j<dstLength;++j) 23 { 24 dstHash+= powValue[dstLength-j-1]*(dst[j]-'a'); 25 } 26 27 //首先计算第一个子串的hash值 28 hashValue[0]=0; 29 for(int j = 0;j<dstLength;++j) 30 { 31 hashValue[0]+= powValue[dstLength-j-1]*(src[j]-'a'); 32 } 33 if(hashValue[0]==dstHash) 34 return 0; 35 for(int i =1;i<srcLength;++i) 36 { 37 //通过前一个子串的hash值计算当前的hash值 38 hashValue[i]=(hashValue[i-1]-powValue[dstLength-1]*(src[i-1]-'a'))*26+(src[i+dstLength-1]-'a'); 39 if(hashValue[i]==dstHash) 40 return i; 41 42 } 43 return -1; 44 } 45 private: 46 int* powValue;//申请内存提前保存26进制值,减少计算时间。 47 int* hashValue;//储存已经计算过的子串的hash值。 48 };
BM(Boyer-Moore)算法
BM算法思想的本质上就是在进行模式匹配的过程中,当模式串与主串的某个字符不匹配的时候,能够跳过一些肯定不会匹配的情况,将模式串往后多滑动几位。
BM算法寻找是否能多滑动几位的原则有两种,分别是 坏字符规则 和 好后缀规则。
坏字符规则:
我们从模式串的末尾往前倒着匹配,当我们发现某个字符无法匹配时,我们把这个无法匹配的字符叫做坏字符(主串中的字符)。此时记录下坏字符在模式串中的位置si,然后拿坏字符在模式串中查找,如果模式串中并不存在这个字符,那么可以将模式串直接向后滑动m位,如果坏字符在模式串中存在,则记录下其位置xi,那么模式串向后移动的位数就是si-xi,(可以在确保si>xi,执行减法,不会出现向前移动的情况)。如果坏字符在模式串中多次出现,那我们在计算xi的时候,选择最靠后的那个,这样不会因为让模式串滑动过多,导致本来可能匹配的情况被略过。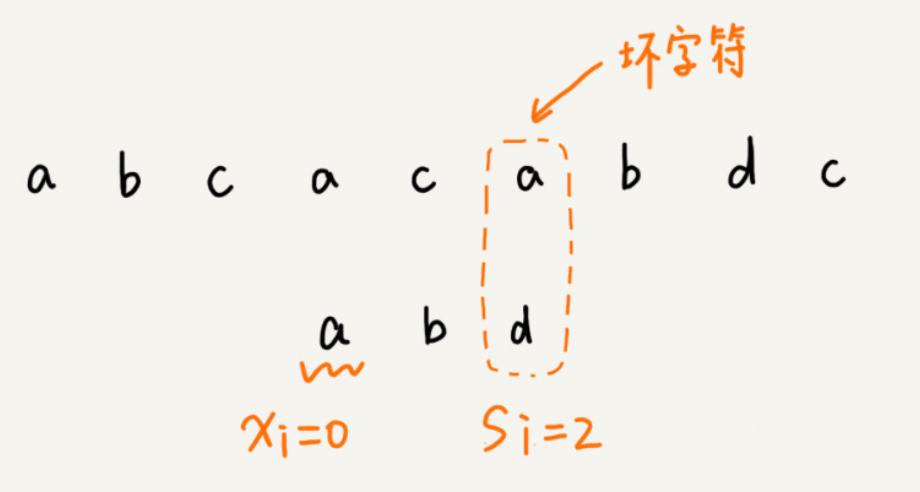
好后缀规则:
在我们反向匹配模式串时,遇到不匹配时,记录下当前位置j位坏字符位置。把已经匹配的字符串叫做好后缀,记作{u}。我们拿它在模式串中查找,如果找到了另一个跟{u}相匹配的字串{u*}, 那么我们就将模式串滑动到字串{u*}与主串{u}对齐的位置。如下图所示: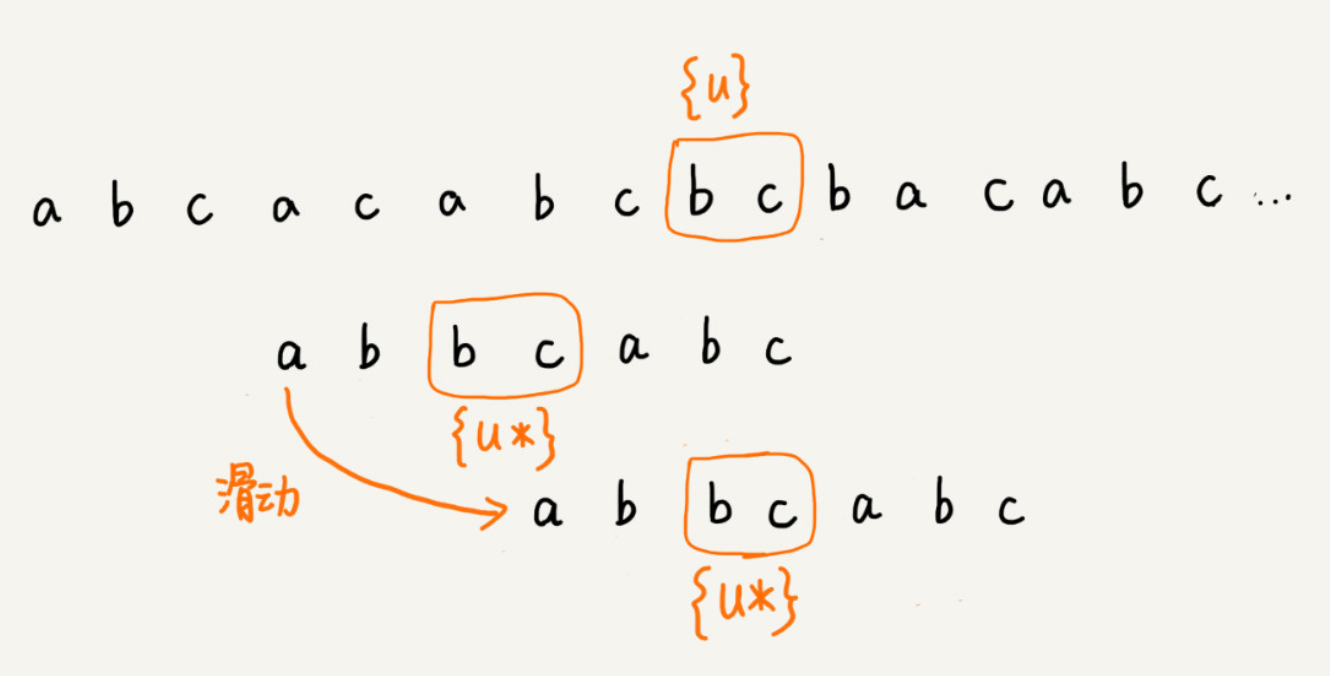
如果在模式串中找不到另一个等于{u}的子串,我们就直接将模式串滑动到主串中{u}的后面,因为之前的任何一次往后滑动,都没有匹配主串中{u}的情况。但是这种滑动做法有点太过头了,可以看下面的例子,如果直接滑动到好后缀的后面,可能会错过模式串与主串可以匹配的情况。如下图:
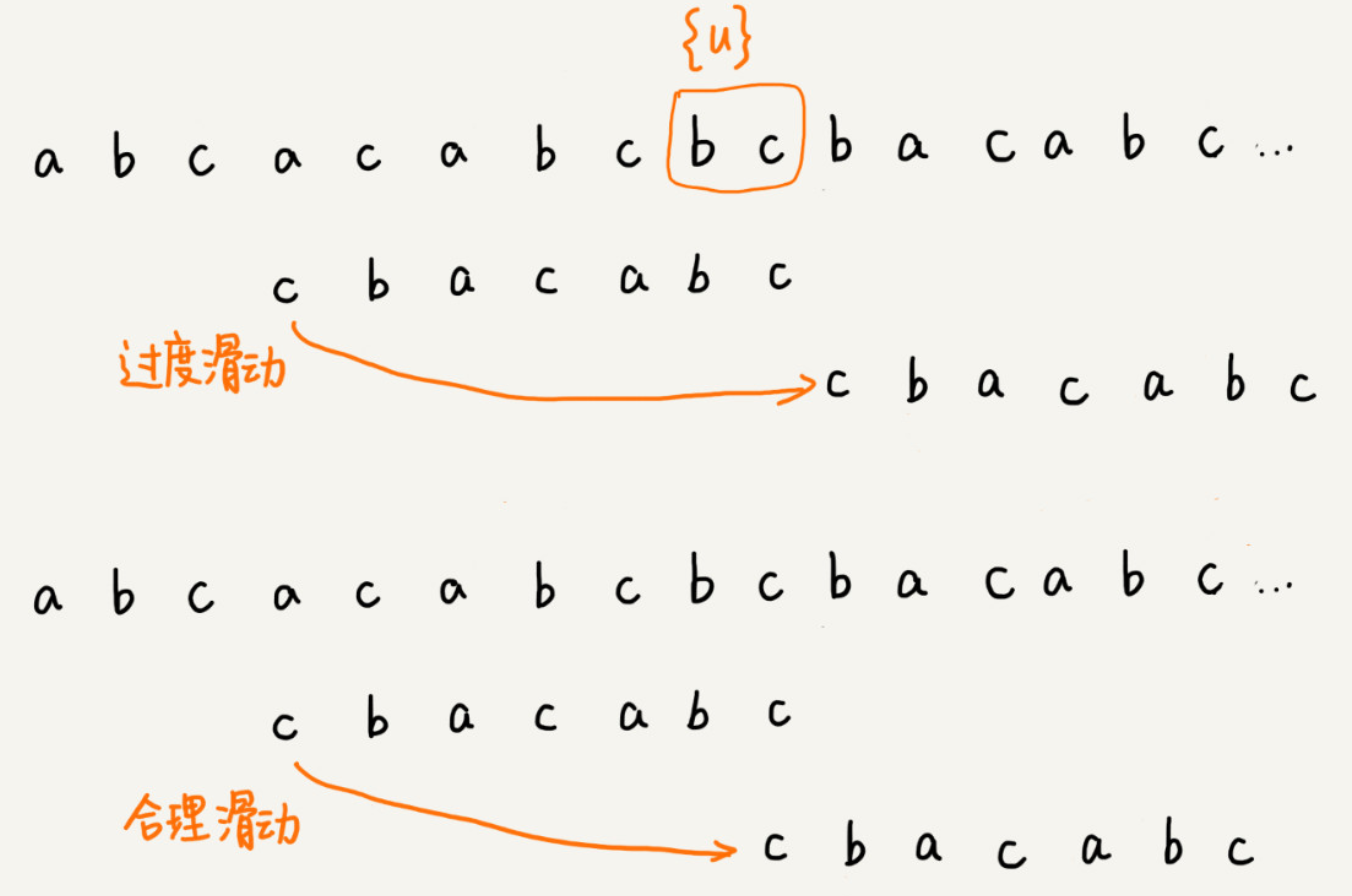
当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候,并且重回部分相等的时候,就可能会存在完全匹配的情况。所以针对这种情况我们不仅要看好后缀在模式串中,是否有另一个匹配的字串,我们还要考察好后缀的后缀字串是否存在跟模式串的前缀字串匹配的情况。如下图所示: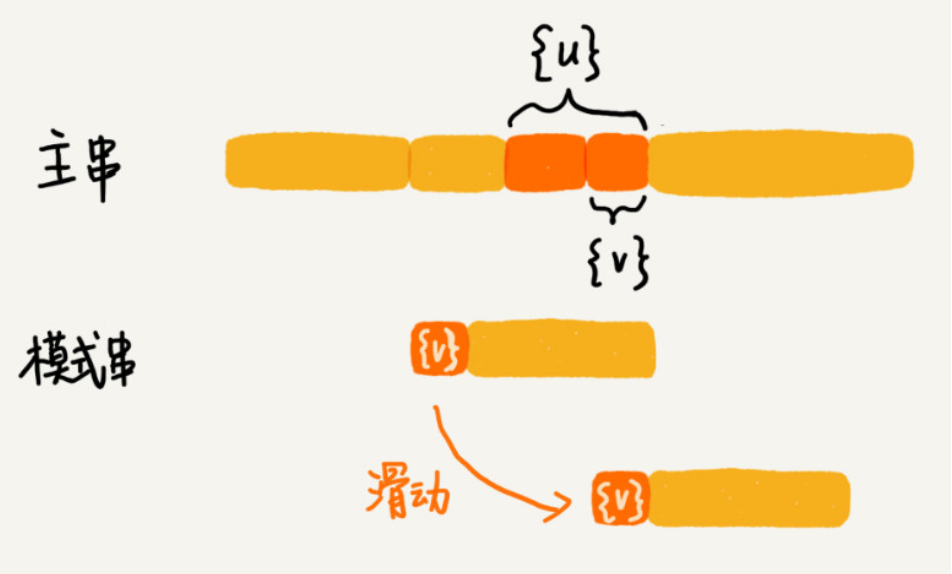
最后总结如何确定模式串向后滑动的位数,我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的。
BM算法性能分析
BM算法的内存消耗:整个算法使用了三个额外数组,其中bc数组的大小和字符集大小有关,suffix数组和prefix数组的大小和模式串长度m有关。
如果我们处理字符集很大的模式匹配问题,bc数组对内存消耗会比较多。好后缀规则和坏字符规则是独立的,如果对内存要求苛刻,那么可以只使用好后缀规则。不过效率也会下降一些。
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 using namespace std; 5 const int size = 256; 6 //将模式串字符使用hash表示 7 void generateBC(char b[], int m, int bc[]){ 8 //b是模式串, m是模式串的长度, bc是散列表 9 //bc的下标是字符集的ASCII码,数组值是每个字符在模式串中出现的位置。 10 for(int i=0; i<size; i++){ 11 bc[i]=-1; 12 } 13 for(int i=0; i<m; i++){ 14 int ascii = (int)b[i]; 15 bc[ascii] = i; 16 } 17 } 18 /* 19 求suffix数组和prefix数组 20 suffix数组的下标K表示后缀字串的长度,数组值对应存储的是,在模式串中跟好后缀{u}相匹配的子串{u*} 21 的起始下标值。 22 prefix数组是布尔型。来记录模式串的后缀字串是否能匹配模式串的前缀子串。 23 24 */ 25 void generateGS(char b[], int m, int suffix[], bool prefix[]){ 26 for(int i=0; i<m;i++){ 27 suffix[i] = -1; 28 prefix[i] = false; 29 } 30 for(int i=0; i<m-1; ++i){ 31 int j = i; 32 int k =0; //公共后缀字串长度 33 while(j >=0 && b[j] == b[m-1-k]){ 34 //与b[0, m-1]求公共后缀字串 35 --j; 36 ++k; 37 suffix[k] = j+1; //j+1表示公共后缀字串在b[0,i]中的起始下标 38 } 39 if(j == -1) prefix[k] = true;//如果公共后缀字串也是模式串的前缀字串 40 41 } 42 } 43 44 //j表示坏字符对应的模式串中的字符下标,m是模式串的长度 45 //计算在好后缀规则下模式串向后移动的个数 46 int moveByGS(int j, int m, int suffix[], bool prefix[]){ 47 int k= m-1-j; //好后缀的长度 48 if(suffix[k] != -1) return j - suffix[k] +1; 49 for(int r = j+2; r<= m-1; ++r){ 50 if(prefix[m-r] == true){ 51 return r; 52 } 53 } 54 return m; 55 } 56 57 //BM算法 58 int BM(char a[], int n, char b[], int m){ 59 int suffix[m]; 60 bool prefix[m]; 61 62 int bc[size];//bc记录模式串中每个字符最后出现的位置 63 64 generateBC(b,m,bc); //构建字符串hash表 65 generateGS(b,m, suffix,prefix); //计算好后缀和好前缀数组 66 67 int i=0; //表示主串与模式串对齐的第一个字符 68 while(i<=n-m){ 69 int j; 70 for(j=m-1; j>=0; j--){ //模式串从后往前匹配 71 if(a[i+j]!= b[j]) break; //坏字符对应的模式串下标是j,即i+j 位置是坏字符的位置si 72 } 73 if(j < 0){ 74 return i; //匹配成功,返回主串与模式串第一个匹配的字符的位置 75 } 76 //这里x等同于将模式串往后滑动j-bc[(int)a[i+j]]位 77 //bc[(int)a[i+j]]表示主串中坏字符在模式串中出现的位置xi 78 int x = i + (j - bc[(int)a[i+j]]); 79 80 int y =0; 81 if(j < m-1){//如果有好后缀的话,计算在此情况下向后移动的位数y 82 y = moveByGS(j, m, suffix, prefix); 83 } 84 i = i + max(x, y); //i更新位可以后移较多的位置 85 86 } 87 return -1; 88 } 89 90 int main(){ 91 char a[] = "aaaabaaba"; 92 char b[] = "aaaa"; 93 int i = BM(a,9,b,2); 94 printf("%d\n", i); 95 return 0; 96 }
KMP算法
KMP 算法的核心思想,跟上一节讲的 BM 算法非常相近。我们假设主串是 a,模式串是 b。在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,我们希望找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况
1 //str1为主串,str2为模式串 2 #include <iostream> 3 #include <string> 4 #include <vector> 5 using namespace std; 6 void getnext(const string &str2,vector<int> next) 7 { next.clear(); 8 next.resize(str2.size()); 9 if (str2.length()== 1) 10 { 11 next[0]=-1; 12 return ; 13 } 14 next[0]=-1; 15 next[1]=0; 16 int len= str2.length(); 17 int i=2,cn=0;//cn为最长前缀的后一个字符 18 while(i<len) 19 { 20 if (str2[i-1]==str2[cn]) //如果前一个字符和cn对应的值相等 21 next[i++]=++cn;//如果相等则此处的值为,cn+1 22 else if (cn>0) 23 cn=next[cn];//不等的话继续往前推 24 else 25 next[i++] =0;//不等的话并未没法往前推就变为0 26 } 27 28 } 29 int kmp( const string &str1, const string &str2,vector<int> & next) 30 { 31 int i1 = 0, i2 = 0; 32 while (i1<str1.length() && i2<str2.length()) 33 { 34 if (str1[i1]==str2[i2])//两者比对,相等则主串和模式串都加加 35 { 36 i1++; 37 i2++; 38 } 39 else if (next[i2]==-1)//两者没有匹配则进一步判断i2是否还有回退的资格,如果等于-1说明已经退到头了,则只能i1++; 40 { 41 i1++; 42 } 43 else//还可以退,则i2回到到next数组指定的位置再进行比对 44 i2=next[i2]; 45 } 46 return i2 == str2.length()?i1-i2:-1; 47 //如果str2已经扫描完了说明已经找到了,返回str1中找到的起始位置;如果没有扫描完说明没有找到返回-1; 48 } 49 int main() 50 { 51 string str1,str2; 52 cin>>str1>>str2; 53 vector<int> next; 54 int k; 55 k=kmp(str1,str2,next); 56 return k; 57 }
Trie树
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
举个简单的例子来说明一下。我们有 6 个字符串,它们分别是:how,hi,her,hello,so,see。我们希望在里面多次查找某个字符串是否存在。如果每次查找,都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配,那效率就比较低,有没有更高效的方法呢?这个时候,我们就可以先对这 6 个字符串做一下预处理,组织成 Trie 树的结构,之后每次查找,都是在 Trie 树中进行匹配查找。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
如果要在一组字符串中,频繁地查询某些字符串,用 Trie 树会非常高效。
构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。
但是一旦构建成功之后,后续的查询操作会非常高效。如果要查询的字符串长度是 k,那我们只需要比对大约 k 个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。
字符串中包含的字符集不能太大,要求字符串的前缀重合比较多,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
代码参考:https://blog.csdn.net/weixin_41427400/article/details/79949422
1 #ifndef TRIETREE_H 2 #define TRIETREE_H 3 4 #include <iostream> 5 #include <string> 6 #include <vector> 7 using namespace std; 8 9 // 定义R为常量 10 const int R = 256; 11 12 // 重定义树节点,便于操作 13 typedef struct TreeNode *Position; 14 15 /* color枚举,储存元素:Red, Black*/ 16 enum Color {Red, Black}; 17 18 /* TrieTree节点 19 * 储存元素: 20 * coloe:节点颜色,红色代表有此单词,黑色代表没有 21 * Next:下一层次节点 22 */ 23 struct TreeNode { 24 Color color; 25 Position Next[R]; 26 }; 27 28 /* TrieTree类(前缀树) 29 * 接口: 30 * MakeEmpty:重置功能,重置整颗前缀树 31 * keys:获取功能,获取TrieTree中的所有单词,并储存在一个向量中 32 * Insert:插入功能,向单词树中插入新的单词 33 * Delete:删除功能,删除单词树的指定单词 34 * IsEmpty:空函数,判断单词树是否为空 35 * Find:查找函数,查找对应的单词,并返回查找情况:查找到返回true,否则返回false 36 * LongestPrefixOf:查找指定字符串的最长前缀单词; 37 * KeysWithPrefix:查找以指定字符串为前缀的单词; 38 * KeysThatMatch:查找匹配对应字符串形式的单词,"."表示任意单词 39 */ 40 class TrieTree 41 { 42 public: 43 // 构造函数 44 TrieTree(); 45 // 析构函数 46 ~TrieTree(); 47 48 // 接口函数 49 void MakeEmpty(); 50 vector <string> keys(); 51 void Insert(string); 52 void Delete(string); 53 54 bool IsEmpty(); 55 bool Find(string) const; 56 string LongestPrefixOf(string) const; 57 vector <string> KeysWithPrefix(string) const; 58 vector <string> KeysThatMatch(string) const; 59 60 private: 61 // 辅助功能函数 62 void MakeEmpty(Position); 63 void Insert(string, Position &, int); 64 void Delete(string, Position &, int); 65 66 Position Find(string, Position, int) const; 67 int Search(string, Position, int, int) const; 68 void Collect(string, Position, vector <string> &) const; // 对应KeysWithPrefix() 69 void Collect(string, string, Position, vector <string> &) const; // 对应KeysThatMatch() 70 71 // 数据成员 72 Position Root; // 储存根节点 73 }; 74 75 #endif
1 #include "TrieTree.h" 2 3 /* 构造函数:初始化对象 4 * 参数:无 5 * 返回值:无 6 */ 7 TrieTree::TrieTree() { 8 Root = new TreeNode(); 9 if (Root == NULL) { 10 cout << "TrieTree申请失败!" << endl; 11 return; 12 } 13 14 // 根节点为黑色节点 15 Root->color = Black; 16 for (int i = 0; i < R; i++) 17 Root->Next[i] = NULL; 18 } 19 20 /* 析构函数:对象消亡时回收储存空间 21 * 参数:无 22 * 返回值:无 23 */ 24 TrieTree::~TrieTree() { 25 MakeEmpty(Root); // 调用重置函数,从树根开始置空 26 } 27 28 /* 重置函数:重置TrieTree 29 * 参数:无 30 * 返回值:无 31 */ 32 void TrieTree::MakeEmpty() { 33 // 将根节点的下一层节点置空 34 for (char c = 0; c < R; c++) 35 if (Root->Next[c] != NULL) 36 MakeEmpty(Root->Next[c]); 37 } 38 39 /* 重置函数:重置指定节点 40 * 参数:tree:想要进行重置额节点 41 * 返回值:无 42 */ 43 void TrieTree::MakeEmpty(Position tree) { 44 // 置空下一层节点 45 for (char c = 0; c < R; c++) 46 if (tree->Next[c] != NULL) 47 MakeEmpty(tree->Next[c]); 48 49 // 删除当前节点 50 delete tree; 51 tree = NULL; 52 } 53 54 /* 获取函数:获单词树中的所有单词,并返回储存的向量 55 * 参数:无 56 * 返回值:vector<string>:储存单词树中所有单词的向量 57 */ 58 vector <string> TrieTree::keys() { 59 // 返回所有以""为前缀的单词,即所有单词 60 return KeysWithPrefix(""); 61 } 62 63 /* 插入函数:向TrieTree中插入指定的单词 64 * 参数:key:想要进行插入的字符串 65 * 返回值:无 66 */ 67 void TrieTree::Insert(string key) { 68 // 从根节点开始递归插入 69 Insert(key, Root, 0); 70 } 71 72 /* 插入驱动函数:将指定的单词进行递归插入 73 * 参数:key:想要进行插入的单词,tree:当前递归节点,d:当前检索的字符索引 74 * 返回值:无 75 */ 76 void TrieTree::Insert(string key, Position &tree, int d) { 77 // 若没有节点则生成新节点 78 if (tree == NULL) { 79 tree = new TreeNode(); 80 if (tree == NULL) { 81 cout << "新节点申请失败!" << endl; 82 return; 83 } 84 85 tree->color = Black; 86 for (int i = 0; i < R; i++) 87 tree->Next[i] = NULL; 88 } 89 90 // 若检索到最后一位,则改变节点颜色 91 if (d == key.length()) { 92 tree->color = Red; 93 return; 94 } 95 96 // 检索下一层节点 97 char c = key[d]; 98 Insert(key, tree->Next[c], d + 1); 99 } 100 101 /* 删除函数:删除TrieTree中的指定单词 102 * 参数:key:想要删除的指定元素 103 * 返回值:无 104 */ 105 void TrieTree::Delete(string key) { 106 // 从根节点开始递归删除 107 Delete(key, Root, 0); 108 } 109 110 /* 删除驱动函数:将指定单词进行递归删除 111 * 参数:key:想要进行删除的单词,tree:当前树节点,d:当前的索引下标 112 * 返回值:无 113 */ 114 void TrieTree::Delete(string key, Position &tree, int d) { 115 // 若未空树则返回 116 if (tree == NULL) 117 return; 118 119 // 检索到指定单词,将其颜色变黑 120 if (d == key.length()) 121 tree->color = Black; 122 123 // 检索下一层节点 124 else { 125 char c = key[d]; 126 Delete(key, tree->Next[c], d + 1); 127 } 128 129 // 红节点直接返回 130 if (tree->color == Red) 131 return; 132 133 // 若未黑节点,且无下层节点则删除该节点 134 for (int i = 0; i < R; i++) 135 if (tree->Next[i] != NULL) 136 return; 137 138 delete tree; 139 tree = NULL; 140 } 141 142 /* 空函数:判断TrieTree是否为空 143 * 参数:无 144 * 返回值:bool:空树返回true,非空返回false 145 */ 146 bool TrieTree::IsEmpty() { 147 for (int i = 0; i < R; i++) 148 if (Root->Next[i] != NULL) 149 return false; 150 return true; 151 } 152 153 /* 查找函数:在TrieTree中查找对应的单词,并返回查找结果 154 * 参数:key:想要查找的单词 155 * 返回值:bool:TrieTree中有key返回true,否则返回false 156 */ 157 bool TrieTree::Find(string key) const { 158 // 查找key最后字符所在节点 159 Position P = Find(key, Root, 0); 160 161 // 无节点则返回false 162 if (P == NULL) 163 return false; 164 165 // 根据节点颜色返回 166 if (P->color == Red) 167 return true; 168 else 169 return false; 170 } 171 172 /* 查找驱动函数:在TrieTree中查找指定的单词并返回其最后的字符所在节点 173 * 参数:key:想要进行查找的单词,tree:当前递归查找的树节点,d:当前检索的索引 174 * 返回值:Position:单词最后字符所在的节点 175 */ 176 Position TrieTree::Find(string key, Position tree, int d) const { 177 // 节点不存在则返回空 178 if (tree == NULL) 179 return NULL; 180 181 // 若检索完成,返回该节点 182 if (d == key.length()) 183 return tree; 184 185 // 检索下一层 186 char c = key[d]; 187 return Find(key, tree->Next[c], d + 1); 188 } 189 190 /* 最长前缀驱动:获取最长前缀在指定字符串中的所有下标 191 * 参数:key:用于查找的字符串,tree:当前的递归节点,d:当前检索的索引,length:当前最长前缀的长度 192 * 返回值:int:最长前缀的长度 193 */ 194 int TrieTree::Search(string key, Position tree, int d, int length) const { 195 // 空树则返回当前前缀的长度 196 if (tree == NULL) 197 return length; 198 199 // 更新前缀长度 200 if (tree->color == Red) 201 length = d; 202 203 // 检索到末尾则返回长度 204 if (d == key.length()) 205 return length; 206 207 // 检索下一层 208 char c = key[d]; 209 return Search(key, tree->Next[c], d + 1, length); 210 } 211 212 /* 最长前缀函数:获取指定字符串中,在TrieTree中存在的最长前缀 213 * 参数:key:想要进行查找的字符串 214 * 返回值:string:最长的前缀单词 215 */ 216 string TrieTree::LongestPrefixOf(string key) const { 217 // 获取最长前缀的下标 218 int Length = Search(key, Root, 0, 0); 219 return key.substr(0, Length); 220 } 221 222 /* 前缀查找驱动:将当前层次所有符合前缀要求的单词存入向量 223 * 参数:key:指定的前缀,tree:当前的节点层次,V:用于储存的向量 224 * 返回值:无 225 */ 226 void TrieTree::Collect(string key, Position tree, vector <string> &V) const{ 227 // 空节点直接返回 228 if (tree == NULL) 229 return; 230 231 // 红节点则压入单词 232 if (tree->color == Red) 233 V.push_back(key); 234 235 // 检索下一层节点 236 for (char i = 0; i < R; i++) 237 Collect(key + i, tree->Next[i], V); 238 } 239 240 /* 前缀查找:查找TrieTree中所有以指定字符串为前缀的单词 241 * 参数:key:指定的前缀 242 * 返回值:vector<string>:储存了所有目标单词的向量 243 */ 244 vector <string> TrieTree::KeysWithPrefix(string key) const { 245 vector <string> V; 246 // 搜集目标单词到向量V 247 Collect(key, Find(key, Root, 0), V); 248 return V; 249 } 250 251 /* 单词匹配驱动:搜集当前层次中所有匹配成功的单词 252 * 参数:pre:匹配前缀单词,pat:用于指定形式的字符串,tree:当前的检索层次,V:用于储存匹配成功单词的向量 253 * 返回值:无 254 */ 255 void TrieTree::Collect(string pre, string pat, Position tree, vector <string> &V) const { 256 // 获取前缀的长度 257 int d = pre.length(); 258 259 // 空树直接返回 260 if (tree == NULL) 261 return; 262 263 // 若前缀长度与指定单词相同且当前节点为红色,则压入前缀 264 if (d == pat.length() && tree->color == Red) 265 V.push_back(pre); 266 267 // 若只是长度相同直接返回 268 if (d == pat.length()) 269 return; 270 271 // 检索下一层节点 272 char next = pat[d]; 273 for (char c = 0; c < R; c++) 274 if (next == '.' || next == c) 275 Collect(pre + c, pat, tree->Next[c], V); 276 } 277 278 /* 单词匹配函数:搜集TrieTree中所以匹配指定字符串形式的单词 279 * 参数:pat:用于指定形式的字符串 280 * 返回值:vector<string>:储存所有目标单词的向量 281 */ 282 vector <string> TrieTree::KeysThatMatch(string pat) const { 283 vector <string> V; 284 // 搜集所有匹配的单词到向量V 285 Collect("", pat, Root, V); 286 return V; 287 }
AC自动机(Aho-Corasick 多模式匹配算法)
假设需要模式串有上万个,通过单模式串匹配算法(比如 KMP 算法),需要扫描几千遍。很显然,这种处理思路比较低效。
Trie 树就是一种多模式串匹配算法。我们用Trie树可以对上千个模式串字典进行预处理,构建成 Trie 树结构。这个预处理的操作只需要做一次,如果字典动态更新了,比如删除、添加了一个模式串,那我们只需要动态更新一下 Trie 树就可以了。
AC 自动机算法,全称是 Aho-Corasick 算法。其实,Trie 树跟 AC 自动机之间的关系,就像单串匹配中朴素的串匹配算法,跟 KMP 算法之间的关系一样,只不过前者针对的是多模式串而已。所以,AC 自动机实际上就是在 Trie 树之上,加了类似 KMP 的 next 数组,只不过此处的 next 数组是构建在树上罢了。
使用Aho-Corasick算法需要三步:
1.建立模式的Trie
2.给Trie添加失败路径
3.根据AC自动机,搜索待处理的文本
下面说明这三步:
1)建立多模式集合的Trie树
Trie树也是一种自动机。对于多模式集合{"say","she","shr","he","her"},对应的Trie树如下,其中红色标记的圈是表示为接收态:
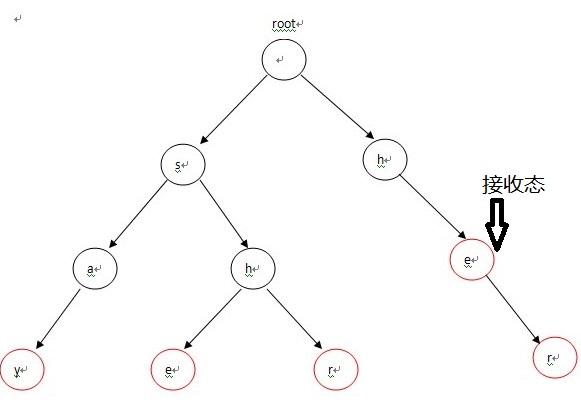
2)为多模式集合的Trie树添加失败路径,建立AC自动机
构造失败指针的过程概括起来就一句话:设这个节点上的字母为C,沿着他父亲的失败指针走,直到走到一个节点,他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字母也为C的儿子。如果一直走到了root都没找到,那就把失败指针指向root。
使用广度优先搜索BFS,层次遍历节点来处理,每一个节点的失败路径。
特殊处理:第二层要特殊处理,将这层中的节点的失败路径直接指向父节点(也就是根节点)。
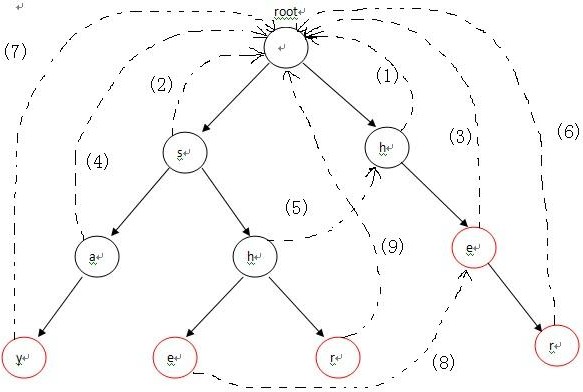
3)根据AC自动机,搜索待处理的文本
从root节点开始,每次根据读入的字符沿着自动机向下移动。
当读入的字符,在分支中不存在时,递归走失败路径。如果走失败路径走到了root节点,则跳过该字符,处理下一个字符。
因为AC自动机是沿着输入文本的最长后缀移动的,所以在读取完所有输入文本后,最后递归走失败路径,直到到达根节点,这样可以检测出所有的模式。
3.Aho-Corasick算法代码示例(https://www.cnblogs.com/xudong-bupt/p/3433506.html)
模式串集合:{"nihao","hao","hs","hsr"}
待匹配文本:"sdmfhsgnshejfgnihaofhsrnihao
1 #include<iostream> 2 #include<string.h> 3 #include<malloc.h> 4 #include <queue> 5 using namespace std; 6 7 typedef struct node{ 8 struct node *next[26]; //接收的态 9 struct node *par; //父亲节点 10 struct node *fail; //失败节点 11 char inputchar; 12 int patterTag; //是否为可接收态 13 int patterNo; //接收态对应的可接受模式 14 }*Tree,TreeNode; 15 char pattern[4][30]={"nihao","hao","hs","hsr"}; 16 17 /** 18 申请新的节点,并进行初始化 19 */ 20 TreeNode *getNewNode() 21 { 22 int i; 23 TreeNode* tnode=(TreeNode*)malloc(sizeof(TreeNode)); 24 tnode->fail=NULL; 25 tnode->par=NULL; 26 tnode->patterTag=0; 27 for(i=0;i<26;i++) 28 tnode->next[i]=NULL; 29 return tnode; 30 } 31 32 /** 33 将Trie树中,root节点的分支节点,放入队列 34 */ 35 int nodeToQueue(Tree root,queue<Tree> &myqueue) 36 { 37 int i; 38 for (i = 0; i < 26; i++) 39 { 40 if (root->next[i]!=NULL) 41 myqueue.push(root->next[i]); 42 } 43 return 0; 44 } 45 46 /** 47 建立trie树 48 */ 49 Tree buildingTree() 50 { 51 int i,j; 52 Tree root=getNewNode(); 53 Tree tmp1=NULL,tmp2=NULL; 54 for(i=0;i<4;i++) 55 { 56 tmp1=root; 57 for(j=0;j<strlen(pattern[i]);j++) ///对每个模式进行处理 58 { 59 if(tmp1->next[pattern[i][j]-'a']==NULL) ///是否已经有分支,Trie共用节点 60 { 61 tmp2=getNewNode(); 62 tmp2->inputchar=pattern[i][j]; 63 tmp2->par=tmp1; 64 tmp1->next[pattern[i][j]-'a']=tmp2; 65 tmp1=tmp2; 66 } 67 else 68 tmp1=tmp1->next[pattern[i][j]-'a']; 69 } 70 tmp1->patterTag=1; 71 tmp1->patterNo=i; 72 } 73 return root; 74 } 75 76 /** 77 建立失败指针 78 */ 79 int buildingFailPath(Tree root) 80 { 81 int i; 82 char inputchar; 83 queue<Tree> myqueue; 84 root->fail=root; 85 for(i=0;i<26;i++) ///对root下面的第二层进行特殊处理 86 { 87 if (root->next[i]!=NULL) 88 { 89 nodeToQueue(root->next[i],myqueue); 90 root->next[i]->fail=root; 91 } 92 } 93 94 Tree tmp=NULL,par=NULL; 95 while(!myqueue.empty()) 96 { 97 tmp=myqueue.front(); 98 myqueue.pop(); 99 nodeToQueue(tmp,myqueue); 100 101 inputchar=tmp->inputchar; 102 par=tmp->par; 103 104 while(true) 105 { 106 if(par->fail->next[inputchar-'a']!=NULL) 107 { 108 tmp->fail=par->fail->next[inputchar-'a']; 109 break; 110 } 111 else 112 { 113 if(par->fail==root) 114 { 115 tmp->fail=root; 116 break; 117 } 118 else 119 par=par->fail->par; 120 } 121 } 122 } 123 return 0; 124 } 125 126 /** 127 进行多模式搜索,即搜寻AC自动机 128 */ 129 int searchAC(Tree root,char* str,int len) 130 { 131 TreeNode *tmp=root; 132 int i=0; 133 while(i < len) 134 { 135 int pos=str[i]-'a'; 136 if (tmp->next[pos]!=NULL) 137 { 138 tmp=tmp->next[pos]; 139 if(tmp->patterTag==1) ///如果为接收态 140 { 141 cout<<i-strlen(pattern[tmp->patterNo])+1<<'\t'<<tmp->patterNo<<'\t'<<pattern[tmp->patterNo]<<endl; 142 } 143 i++; 144 } 145 else 146 { 147 if(tmp==root) 148 i++; 149 else 150 { 151 tmp=tmp->fail; 152 if(tmp->patterTag==1) //如果为接收态 153 cout<<i-strlen(pattern[tmp->patterNo])+1<<'\t'<<tmp->patterNo<<'\t'<<pattern[tmp->patterNo]<<endl; 154 } 155 } 156 } 157 while(tmp!=root) 158 { 159 tmp=tmp->fail; 160 if(tmp->patterTag==1) 161 cout<<i-strlen(pattern[tmp->patterNo])+1<<'\t'<<tmp->patterNo<<'\t'<<pattern[tmp->patterNo]<<endl; 162 } 163 return 0; 164 } 165 166 /** 167 释放内存,DFS 168 */ 169 int destory(Tree tree) 170 { 171 if(tree==NULL) 172 return 0; 173 queue<Tree> myqueue; 174 TreeNode *tmp=NULL; 175 176 myqueue.push(tree); 177 tree=NULL; 178 while(!myqueue.empty()) 179 { 180 tmp=myqueue.front(); 181 myqueue.pop(); 182 183 for (int i = 0; i < 26; i++) 184 { 185 if(tmp->next[i]!=NULL) 186 myqueue.push(tmp->next[i]); 187 } 188 free(tmp); 189 } 190 return 0; 191 } 192 193 int main() 194 { 195 char a[]="sdmfhsgnshejfgnihaofhsrnihao"; 196 Tree root=buildingTree(); ///建立Trie树 197 buildingFailPath(root); ///添加失败转移 198 cout<<"待匹配字符串:"<<a<<endl; 199 cout<<"模式"<<pattern[0]<<" "<<pattern[1]<<" "<<pattern[2]<<" "<<pattern[3]<<" "<<endl<<endl; 200 cout<<"匹配结果如下:"<<endl<<"位置\t"<<"编号\t"<<"模式"<<endl; 201 searchAC(root,a,strlen(a)); ///搜索 202 destory(root); ///释放动态申请内存 203 return 0; 204 }
Hyperscan
Hyperscan是一款来自于Intel的高性能的正则表达式匹配库。它是基于X86平台以PCRE为原型而开发的,并以BSD许可开源在https://01.org/hyperscan。在支持PCRE的大部分语法的前提下,Hyperscan增加了特定的语法和工作模式来保证其在真实网络场景下的实用性。与此同时,大量高效算法及IntelSIMD*指令的使用实现了Hyperscan的高性能匹配。Hyperscan适用于部署在诸如DPI/IPS/IDS/FW等场景中,目前已经在全球多个客户网络安全方案中得到实际的应用。此外,Hyperscan还支持和开源IDS/IPS产品Snort(https://www.snort.org)和Suricata (https://suricata-ids.org)集成,使其应用更加广泛。
原理
Hyperscan以自动机理论为基础,其工作流程主要分成两个部分:编译期(compiletime)和运行期(run-time)。
编译期
Hyperscan 自带C++编写的正则表达式编译器。如图1所示,它将正则表达式作为输入,针对不同的IA平台,用户定义的模式及特殊语法,经过复杂的图分析及优化过程,生成对应的数据库。另外,生成的数据库可以被序列化后保存在内存中,以供运行期提取使用。
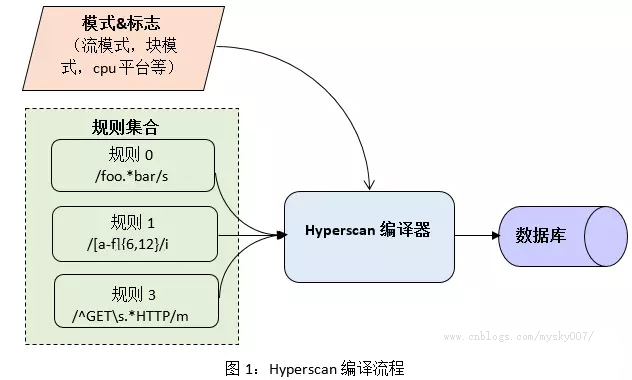
运行期
Hyperscan的运行期是通过C语言来开发的。图2展示了Hyperscan在运行期的主要流程。用户需要预先分配一段内存来存储临时匹配状态信息,之后利用编译生成的数据库调用Hyperscan内部的匹配引擎(NFA, DFA等)来对输入进行模式匹配。Hyperscan在引擎中使用Intel处理器所具有的SIMD指令进行加速。同时,用户可以通过回调函数来自定义匹配发生后采取的行为。由于生成的数据库是只读的,用户可以在多个CPU核或多线程场景下共享数据库来提升匹配扩展性。
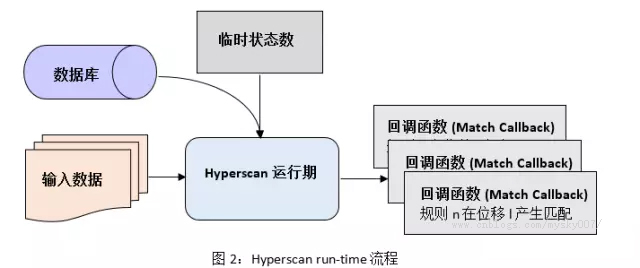
特点
功能多样
作为纯软件产品,Hyperscan支持Intel处理器多平台的交叉编译,且对操作系统无特殊限定,同时支持虚拟机和容器场景。Hyperscan 实现了对PCRE语法的基本涵盖,对复杂的表达式例如”.*”和”[^>]*”不会有任何支持问题。在此基础上,Hyperscan增加了不同的匹配模式(流模式和块模式)来满足不同的使用场景。通过指定参数,Hyperscan能找到匹配的数据在输入流中的起始和结束位置。更多功能信息请参考http://01org.github.io/hyperscan/dev-reference/。
大规模匹配
根据规则复杂度的不同,Hyperscan能支持几万到几十万的规则的匹配。与传统正则匹配引擎不同,Hyperscan支持多规则的同步匹配。在用户为每条规则指定独有的编号后,Hypercan可以将所有规则编译成一个数据库并在匹配过程中输出所有当前匹配到的规则信息。
流模式(streaming mode)
Hyperscan主要分为两种模式:块模式 (blockmode)和流模式 (streaming mode). 其中块模式为状态正则匹配引擎具有的模式,即对一段现成的完整数据进行匹配,匹配结束即返回结果。流模式是Hyperscan为网络场景下跨报文匹配设计的特殊匹配模式。在真实网络场景下,数据是分散在多报文中。若有数据在尚未到达的报文中时,传统匹配模式将无法适用。在流模式下,Hyperscan可以保存当前数据匹配的状态,并以其作为接收到新数据时的初始匹配状态。如图3所示,不管数据”xxxxabcxxxxxxxxdefx”以怎样的形式被分散在以时间顺序到达的报块中,流模式保证了最后匹配结果的一致性。另外,Hyperscan对保存的匹配状态进行了压缩以减少流模式对内存的占用。Hyperscan流模式解决了数据完整性问题,极大地简化用户网络流处理的过程。

高性能及高扩展性
Hyperscan在不同规则集下,单核性能可实现3.6Gbps~23.9Gbps。而且Hyperscan具有良好的扩展性,随着使用核数的增加,匹配性能基本处于线性增长的趋势。在网络场景中,同一规则库往往需要匹配多条网络流。Hypercan的高扩展性为此提供了有力的支持。
Hyperscan与DPDK的整合方案
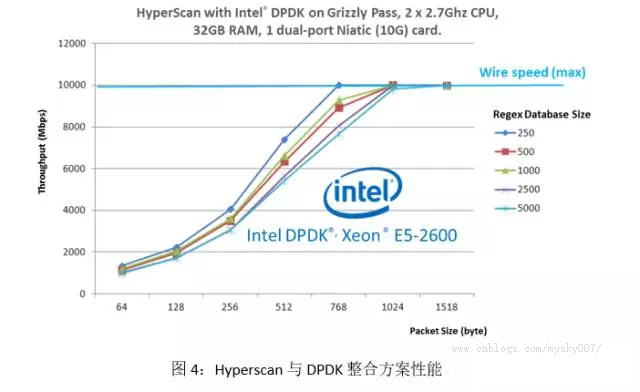
DPDK (http://dpdk.org)作为高速网络报文处理转发套件,在业界得到了极为广泛的应用。Hyperscan能与DPDK整合成为一套高性能的DPI解决方案。图4展示了Hyperscan与DPDK整合后的性能数据。我们在测试中使用了真实的规则库并以http流量作为输入。Hyperscan与DPDK的结合实现了较高的性能,且随着包大小的增长,性能可以到达物理的极限值。
pcre VS hyperscan对比
PCRE简介
PCRE是Perl Compatible Regular Expressions的简称,是一款十分流行的用C语言编写的正则表达式匹配库,其灵感来源于Perl语言中的正则表达式功能,其语法比POSIX和其他许多正则表达式库更强大更灵活。
测试结果及分析:
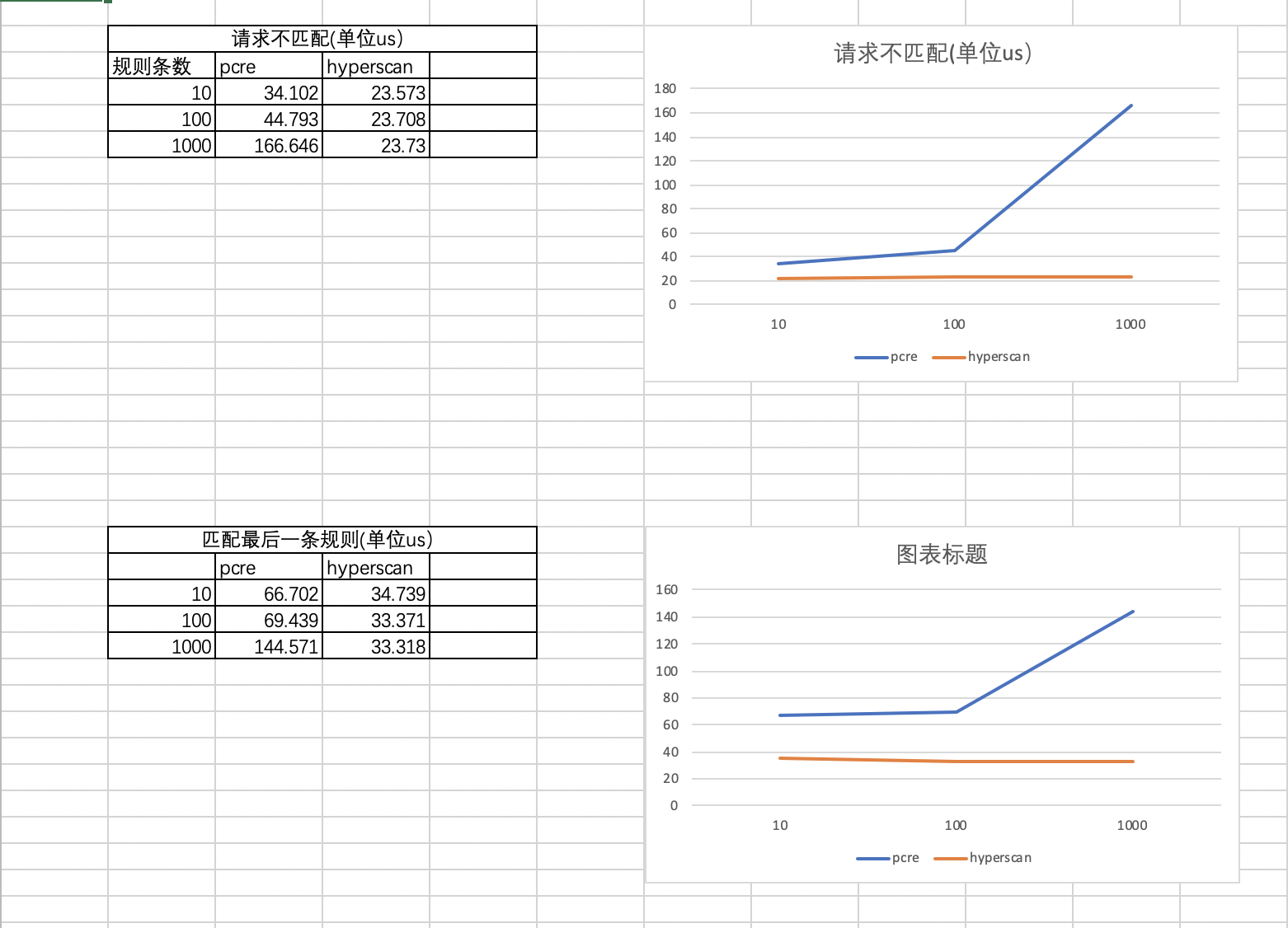
从以上结果中分析得知: 1.hyperscan性能优于pcre; 2.pcre由于是串行匹配多条规则,因此会随着规则数的增加,性能线性下降, hyperscan则不会; 3.匹配最后一条规则时性能较不匹配要低; 4.hyperscan占用的静态空间和动态空间都会大于pcre; 由于hyperscan是静态库同时又较大,所以编译出来的bin文件会比较大,在选型时可以考虑在规则量小时用pcre,当规则数量达到千条以上时再用hyperscan替换性价比较高
测试方法说明
1.规则数按10、100、1000分布; 2.分别统计匹配耗时输出到文件; 3.每轮测试发送1000条请求; 4.统计输出耗时的平均值;
展望:Hyperscan与Snort的集成
Hyperscan作为一款高性能的正则表达式匹配库,非常适用于部署在诸如DPI/IPS/IDS/NGFW等网络解决方案中。Snort (https://www.snort.org) 是目前应用最为广泛的开源IDS/IPS产品之一,其核心部分涉及到大量纯字符串及正则表达式的匹配工作。Hyperscan集成到Snort中将显著提升Snort的总体性能
Snort简介

如图1所示,Snort主要分成五个部分。报文解析器负责从不同的网络接口接收到报文,并对报文内容进行初步的解析。预处理器是对解析过的报文进一步处理的插件,其功能包括HTTP URI归一化,报文整合,TCP流重组等。检测引擎是Snort当中最为核心的部分。它根据现有的规则,对报文数据进行匹配。匹配的性能对Snort总体性能起着至关重要的作用。假如匹配成功,则依据规则中定义的行为通知日志及报警系统。该系统可输出相应的警报或者日志。用户也可以定义输出模块来以特定形式(例如数据库,XML文件)保存警报或日志。
Hyperscan 的集成

如图2所示,Hyperscan与Snort的集成主要集中在以下四个方面:
纯字符串匹配
用户可以在Snort规则中定义匹配特定的字符串,并在相应报文中寻找该字符串。Snort中采用了Boyer-Moore算法进行匹配。我们用Hyperscan对这一算法进行替换以提升匹配性能。
PCRE匹配
Snort中使用了PCRE来作为正则表达式匹配的引擎。Hyperscan兼容了PCRE的语法规则,但不支持少数回溯及断言语法。但是Hyperscan本身自带有PCRE的预处理功能(PCRE Prefiltering),可以通过对PCRE规则进行变换以兼容Hyperscan。实际规则产生的匹配是变换后的规则所产生匹配的子集。因此可以使用Hyperscan进行预先扫描,若不产生匹配则实际规则也无匹配。若产生了匹配,可以通过PCRE的扫描来确认是否有真正的匹配。由于Hyperscan的总体性能高于PCRE,Hyperscan的预先过滤可以避免PCRE匹配带来的过大时间开销。
多字符串匹配
Snort中另外一个重要的匹配过程是多字符串的匹配。多字符串的匹配可以快速过滤掉无法匹配的规则以减少需要逐条匹配的规则数从而提升匹配的性能。Snort中使用了Aho-Corasick算法进行多字符串的匹配。我们用Hyperscan替代了这一算法并且带来了显著的性能提升。
Http预处理
除了引擎的匹配算法的集成,我们在预处理器中也添加了Hyperscan。在做Http预处理时,我们利用了Hyperscan搜索相关关键字来进一步加速预处理的流程。
性能数据
我们选取了Snort自带的VRT 规则(8683条)作为测试规则,同时以存有真实网络流量信息的PCAP文件作为输入进行测试。图3展示了在Broadwell-EP平台下,原生Snort和经过Hyperscan加速的Snort在单核单线程下的性能对比。我们可以看到,Hyperscan极大提升了Snort的匹配性能,总体性能约是原始Snort性能的6倍。另外,我们对原生Snort与经过Hyperscan优化后的Snort在内存消耗方面进行了比较。由于原生Snort依赖于Aho-Corasick算法,需要将所有规则转化成Trie树结构,因此占用较大的内存。而Hyperscan拥有自身优化过的匹配引擎进行匹配,大量减少了匹配过程中对内存的消耗。如图4所示,在这个测试中,总体上原始Snort所占用的内存是经过Hyperscan优化后的Snort的12倍。


参考
数据结构与算法之美 王争
Intel高性能正则表达式匹配库——Hyperscan
https://zhuanlan.zhihu.com/p/40603962
http://www.cs.jhu.edu/~langmea/resources/lecture_notes/boyer_moore.pdf
A new proof of the linearity of the Boyer-Moore string searching algorithm
Tight bounds on the complexity of the Boyer-Moore string matching algorithm


