跳表

如何理解“跳表”？

对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也只能从头到尾遍历链表。这样查找效率就会很低，时间复杂度会很高，是 O(n)。

 

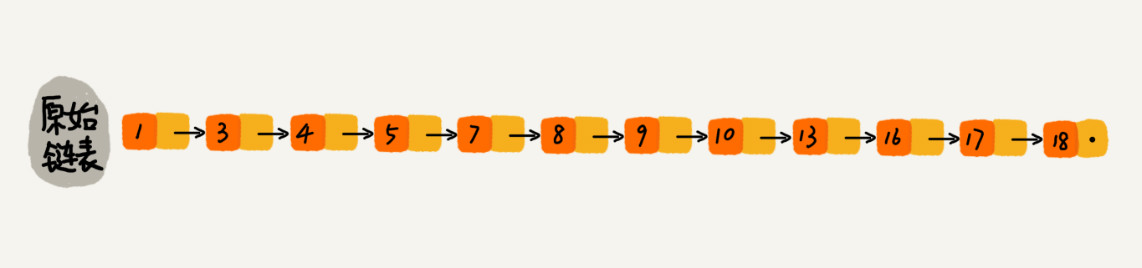
 那怎么来提高查找效率呢？如果像图中那样，对链表建立一级“索引”，查找起来是不是就会更快一些呢？

每两个结点提取一个结点到上一级，我们把抽出来的那一级叫作索引或索引层。你可以看我画的图。图中的 down 表示 down 指针，指向下一级结点。

 

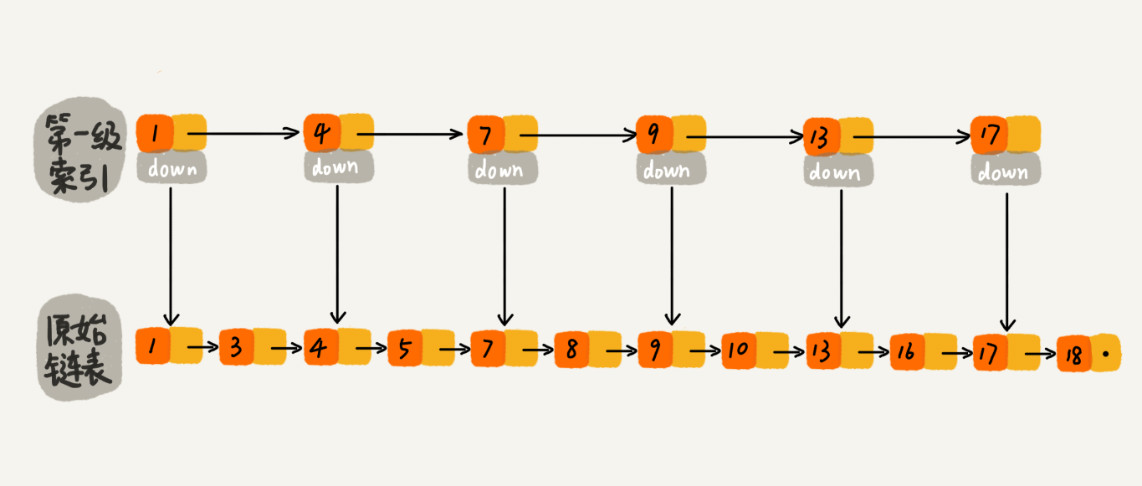
如果我们现在要查找某个结点，比如 16。我们可以先在索引层遍历，当遍历到索引层中值为 13 的结点时，我们发现下一个结点是 17，那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针，下降到原始链表这一层，继续遍历。这个时候，我们只需要再遍历 2 个结点，就可以找到值等于 16 的这个结点了。这样，原来如果要查找 16，需要遍历 10 个结点，现在只需要遍历 7 个结点

从这个例子里，我们看出，加来一层索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了

用跳表查询到底有多快？

每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，第三级索引的结点个数大约就是 n/8，依次类推，也就是说，第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2，那第 k级索引结点的个数就是 n/(2k)

假设索引有 h 级，最高级的索引有 2 个结点。通过上面的公式，我们可以得到 n/(2h)=2，从而求得 h=log2n-1。如果包含原始链表这一层，整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)

那这个 m 的值是多少呢？按照前面这种索引结构，我们每一级索引都最多只需要遍历 3 个结点，也就是说 m=3，为什么是 3 呢？我来解释一下。

假设我们要查找的数据是 x，在第 k 级索引中，我们遍历到 y 结点之后，发现 x 大于 y，小于后面的结点 z，所以我们通过 y 的 down 指针，从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中，y 和 z 之间只有 3 个结点（包含 y 和 z），所以，我们在 K-1 级索引中最多只需要遍历 3 个结点，依次类推，每一级索引都最多只需要遍历 3 个结点

 

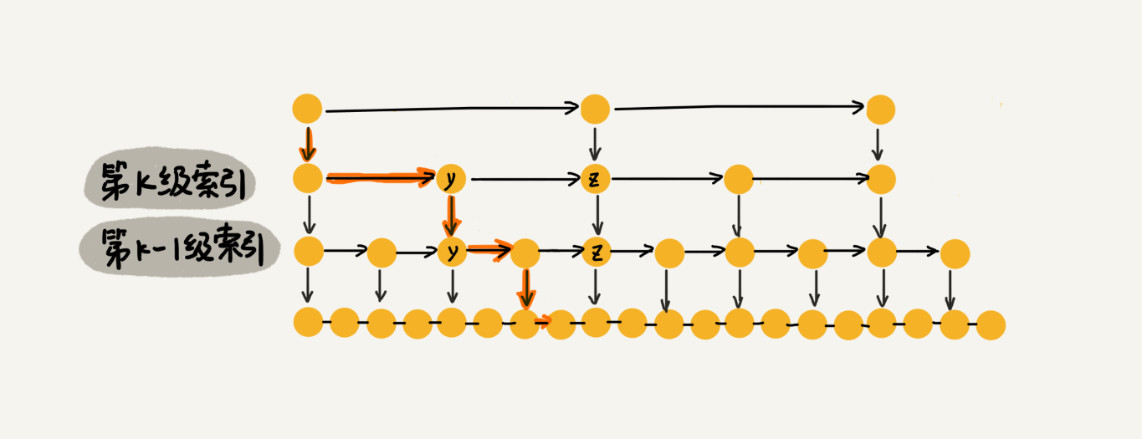
 通过上面的分析，我们得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 O(logn)

插入操作

先确定该元素要占据的层数 K（采用丢硬币的方式，这完全是随机的）。

然后在 Level 1 ... Level K 各个层的链表都插入元素。

用Update数组记录插入位置，同样从顶层开始，逐层找到每层需要插入的位置，再生成层数并插入。

例子：插入 119， K = 2

 

void insert(int key)
{
    int p = head;
    int update[MAX_LEVEL + 5];
    int k = rand_level();
    for (register int i = MAX_LEVEL; i; --i)
    {
        while (sl[p].next[i] ^ tail && sl[sl[p].next[i]].key < key)
            p = sl[p].next[i];
        update[i] = p;
    }
    int temp;
    new_node(temp, key);
    for (register int i = k; i; --i)
    {
        sl[temp].next[i] = sl[update[i]].next[i];
        sl[update[i]].next[i] = temp;
    }
}

 

查询操作

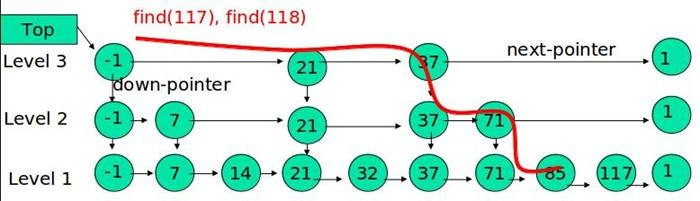
从最上层开始，如果key小于或等于当层后继节点的key,则平移一位；如果key更大，则层数减1，继续比较。最终一定会到第一层（想想为什么）

 

删除操作

void erase(int key)
{
    int p = head;
    int update[MAX_LEVEL + 5];
    for (register int i = MAX_LEVEL; i; --i)
    {
        while (sl[p].next[i] ^ tail && sl[sl[p].next[i]].key < key)
            p = sl[p].next[i];
        update[i] = p;
    }
    free_node(sl[p].next[1]);
    for (register int i = MAX_LEVEL; i; --i)
    {
        if (sl[sl[update[i]].next[i]].key == key)
            sl[update[i]].next[i] = sl[sl[update[i]].next[i]].next[i];
    }
}

 

实例

题目：给出 n 个正整数，然后有 m 个询问，每个询问一个整数，询问该整数是否在 n 个正整数中出现过。

思路：用set就能实现，这里尝试用跳表（set本部就是平衡树，所有用SkipList能解决的，set也能解决一些）

 

#include<cstdio>
#include<cstdlib>
using namespace std;

const int maxn = 100000 + 10;
const int max_level = 25;        //层数上限

//定义节点
struct Node
{
    int key;
    int next[max_level + 1];  //next[i]表示这个节点在第i层的下一个编号
}node[maxn + 2];
int node_tot, head, tail;

//生成层数
inline int rand_level()
{
    int ret = 1;
    while (rand() % 2 && ret <= max_level)
        ret++;
    return ret;
}

//分配新节点  //key默认为0，表示head、tail的值为0
inline void new_node(int& p, int key = 0)
{
    p = ++node_tot;
    node[p].key = key;
}


//初始化
inline void init()
{
    new_node(head); new_node(tail);
    for (register int i = 1; i <= max_level; i++)
        node[head].next[i] = tail;
}

//插入操作
void insert(int key)
{
    int p = head;
    int update[max_level + 1];
    int K = rand_level();
    for (register int i = max_level; i; i--)
    {
        while (node[p].next[i] ^ tail && node[node[p].next[i]].key < key)  p = node[p].next[i];
        update[i] = p;
    }
    int tmp;
    new_node(tmp, key);
    for (register int i = K; i; i--)
    {
        node[tmp].next[i] = node[update[i]].next[i];
        node[update[i]].next[i] = tmp;
    }
}

//查找元素
int find(int key)
{
    int p = head;
    for(register int i = max_level; i; i--)
    {
        while (node[p].next[i] ^ tail && node[node[p].next[i]].key < key)
            p = node[p].next[i];
    }
    if (node[node[p].next[1]].key == key)  return node[p].next[1] - 2;
    else return -1;
}

int n, m;

int main()
{
    srand(19260817);
    scanf("%d%d", &n, &m);
    init();
    int tmp;
    while (n--)
    {
        scanf("%d", &tmp);
        insert(tmp);
    }
    while (m--)
    {
        scanf("%d", &tmp);
        int res = find(tmp);
        if (res > 0)  printf("YES\n"); 
        else  printf("NO\n");
    }
    return 0;
}

 

实例2

package skiplist;
 
import java.util.Random;
 
/**
 * 跳表的一种实现方法。
 * 跳表中存储的是正整数，并且存储的是不重复的。
 *
 * Author：ZHENG
 */
public class SkipList {
 
  private static final int MAX_LEVEL = 16;
 
  private int levelCount = 1;
 
  private Node head = new Node();  // 带头链表
 
  private Random r = new Random();
 
  public Node find(int value) {
    Node p = head;
    for (int i = levelCount - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
    }
 
    if (p.forwards[0] != null && p.forwards[0].data == value) {
      return p.forwards[0];
    } else {
      return null;
    }
  }
 
  public void insert(int value) {
    int level = randomLevel();
    Node newNode = new Node();
    newNode.data = value;
    newNode.maxLevel = level;
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
      update[i] = head;
    }
 
    // record every level largest value which smaller than insert value in update[]
    Node p = head;
    for (int i = level - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
      update[i] = p;// use update save node in search path
    }
 
    // in search path node next node become new node forwords(next)for (int i = 0; i < level; ++i) {
      newNode.forwards[i] = update[i].forwards[i];
      update[i].forwards[i] = newNode;
    }
 
    // update node hightif (levelCount < level) levelCount = level;
  }
 
  public void delete(int value) {
    Node[] update = new Node[levelCount];
    Node p = head;
    for (int i = levelCount - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
      update[i] = p;
    }
 
    if (p.forwards[0] != null && p.forwards[0].data == value) {
      for (int i = levelCount - 1; i >= 0; --i) {
        if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
          update[i].forwards[i] = update[i].forwards[i].forwards[i];
        }
      }
    }
  }
 
  // 随机 level 次，如果是奇数层数 +1，防止伪随机private int randomLevel() {
    int level = 1;
    for (int i = 1; i < MAX_LEVEL; ++i) {
      if (r.nextInt() % 2 == 1) {
        level++;
      }
    }
 
    return level;
  }
 
  public void printAll() {
    Node p = head;
    while (p.forwards[0] != null) {
      System.out.print(p.forwards[0] + " ");
      p = p.forwards[0];
    }
    System.out.println();
  }
 
  public class Node {
    private int data = -1;
    private Node forwards[] = new Node[MAX_LEVEL];
    private int maxLevel = 0;
 
    @Override
    public String toString() {
      StringBuilder builder = new StringBuilder();
      builder.append("{ data: ");
      builder.append(data);
      builder.append("; levels: ");
      builder.append(maxLevel);
      builder.append(" }");
 
      return builder.toString();
    }
  }
 
}