ASDFZ 3634 -- 小 X 的二叉树
Description
小 X 又回忆起和小 R 在一起的时光……
当时小 X 正在研究一种二叉树……
小 X 研究的二叉树是一棵有 n 个点的 Δk 树。
小 X 认为,没有点权的二叉树是没有灵魂的,于是这棵树第 i 个点有点权 ai。
小 X 认为,一棵二叉树是 Δk 树,当且仅当任意一个点的点权和它的所有祖先的点权的差的绝对值都不超过 kkk。
显然地,如果一棵二叉树是 Δk 树,那么它一定是 Δ(k+1)树。
小 X 认为,一棵 Δk 树按照如下方式递归构成的序列一定有优美的性质:
![]()
如上图,2,7,15,8,9,5即为该树中序遍历得到的点权序列。
然而趁小 X 想着这个二叉树睡着的时候,小 R 把他的树删了。
小 X 醒后发现自己的树不见了,还好中序遍历得到的点权序列 p 还在。小 X 想让你帮他检查一下,这个序列是否可以通过一棵 Δk 树中序遍历得到。
当时小 X 正在研究一种二叉树……
小 X 研究的二叉树是一棵有 n 个点的 Δk 树。
小 X 认为,没有点权的二叉树是没有灵魂的,于是这棵树第 i 个点有点权 ai。
小 X 认为,一棵二叉树是 Δk 树,当且仅当任意一个点的点权和它的所有祖先的点权的差的绝对值都不超过 kkk。
显然地,如果一棵二叉树是 Δk 树,那么它一定是 Δ(k+1)树。
小 X 认为,一棵 Δk 树按照如下方式递归构成的序列一定有优美的性质:
- 递归进入左子树。
- 将该点本身的权值加入序列的末尾。
- 递归进入右子树。
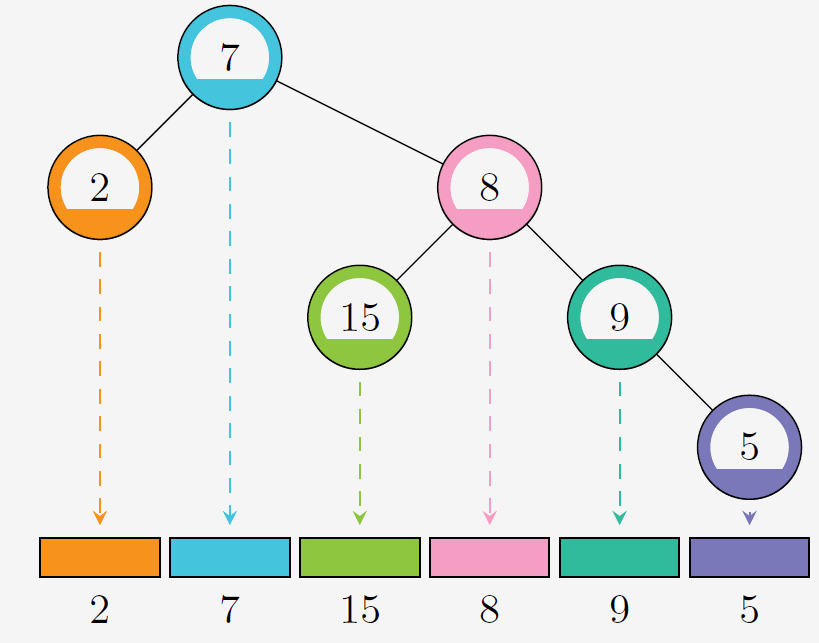
如上图,2,7,15,8,9,5即为该树中序遍历得到的点权序列。
然而趁小 X 想着这个二叉树睡着的时候,小 R 把他的树删了。
小 X 醒后发现自己的树不见了,还好中序遍历得到的点权序列 p 还在。小 X 想让你帮他检查一下,这个序列是否可以通过一棵 Δk 树中序遍历得到。
Input
从标准输入读入数据。
多组数据,第一行一个正整数 T 表示数据组数。
每组数据包括两行:
第一行两个正整数 n,k表示这棵二叉树的点数和这是一棵 Δk 树。
第二行 n 个用空格隔开的非负整数,第 iii 个整数表示中序遍历得到的第 i 个点权 pi。
多组数据,第一行一个正整数 T 表示数据组数。
每组数据包括两行:
第一行两个正整数 n,k表示这棵二叉树的点数和这是一棵 Δk 树。
第二行 n 个用空格隔开的非负整数,第 iii 个整数表示中序遍历得到的第 i 个点权 pi。
Output
输出到标准输出。
每组数据输出一行,如果这个序列可以通过一棵 Δk 树中序遍历得到,输出
每组数据输出一行,如果这个序列可以通过一棵 Δk 树中序遍历得到,输出
Yes,否则输出 No。Sample Input
3
6 10
2 7 15 8 9 5
6 8
2 7 15 8 9 5
6 7
2 7 15 8 9 5
6 10
2 7 15 8 9 5
6 8
2 7 15 8 9 5
6 7
2 7 15 8 9 5
Sample Output
Yes
Yes
No
Yes
No
Sample Explanation
这棵树就是【题目描述】中图片里的那棵树。
Hint
对于 10% 的数据,1≤n≤5。
对于 30% 的数据,1≤n≤200。
对于 60%的数据,1≤n≤5000。
对于 100% 的数据,1≤n≤2×10^5,1≤∑n≤10^6,0≤pi,k≤10^9,1≤T≤6。
对于 30% 的数据,1≤n≤200。
对于 60%的数据,1≤n≤5000。
对于 100% 的数据,1≤n≤2×10^5,1≤∑n≤10^6,0≤pi,k≤10^9,1≤T≤6。
Source
2019NOIP前训练
思路
树的形式,实为分治,比较大小,总结结论题(不一定是递推),分治赛高(min,max程序可复制更改,但一定要仔细!!!)
代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=200010;
int t,n,k,p[N];
int s1[N][20],s2[N][20];
void maxs() {
for(int i=1; i<=n; i++)
s1[i][0]=p[i];
for(int j=1; j<=18; j++)
for(int i=1; i<=n; i++) {
if(i+(1<<j)-1>n)
break;
s1[i][j]=max(s1[i][j-1],s1[i+(1<<j-1)][j-1]);
}
}
void mins() {
for(int i=1; i<=n; i++)
s2[i][0]=p[i];
for(int j=1; j<=18; j++)
for(int i=1; i<=n; i++) {
if(i+(1<<j)-1>n)
break;
s2[i][j]=min(s2[i][j-1],s2[i+(1<<j-1)][j-1]);
}
}
int gmn(int l,int r) {
int x=log2(r-l+1);
return min(s2[l][x],s2[r-(1<<x)+1][x]);
}
int gmx(int l,int r) {
int x=log2(r-l+1);
return max(s1[l][x],s1[r-(1<<x)+1][x]);
}
bool check(int l,int r) {
if(l>=r)
return true;
int x=log(r-l+1)/log(2);
int mn=gmn(l,r),mx=gmx(l,r);
for(int i=0; i*2<=r-l; i++) {
if(p[l+i]-k<=mn&&p[l+i]+k>=mx)
return check(l,l+i-1)&&check(l+i+1,r);
if(p[r-i]-k<=mn&&p[r-i]+k>=mx)
return check(r-i+1,r)&&check(l,r-i-1);
}
return false;
}
int main () {
scanf("%d",&t);
while(t--) {
scanf("%d%d",&n,&k);
for(int i=1; i<=n; i++)
scanf("%d",&p[i]);
maxs();
mins();
if(check(1,n))
printf("Yes\n");
else
printf("No\n");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号