P3193 [HNOI2008]GT考试

题目描述

阿申准备报名参加 GT 考试，准考证号为 N 位数X1,X2…Xn(0≤Xi≤9)，他不希望准考证号上出现不吉利的数字。 他的不吉利数学A1,A2…Am(0≤Ai≤9) 有 M 位，不出现是指 X1,X2…Xn​ 中没有恰好一段等于 A1,A2…Am 和X1​ 可以为 0

输入格式

第一行输入N,M,K.接下来一行输入M位的数。

输出格式

阿申想知道不出现不吉利数字的号码有多少种，输出模 K 取余的结果。

输入输出样例

输入 #1

4 3 100
111

输出 #1

81

说明/提示

N≤109,M≤20,K≤1000

思路

源自：蒟蒻のblog

首先，如果n和m没有那么大的话，有一个非常显然的dp做法：

设dp[i][j]]表示长度为i的字符串，最后j个可以匹配模板串前j位的情况数

那么显然，答案就是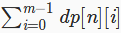了

转移过程则需要用一个辅助数组：令g[i][j]表示模板串的前缀iii可以转移到前缀j的方法数（注意它可能可以转移到很多个串）

辅助数组的生成可以用next数组来推（模板串太短，其实暴力也是可以的）

那么dp[i+1][k]=dp[i][j]∗g[j][k](j=1...m)

然后再看这题的数据范围：n≤10^9

Easy，加一个矩阵快速幂来解决上面的递推就行了

代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N=30;
const int oo=1e9;

char s[N];
int Mod,ans;
int n,m,f[N][10];
int wor[N],a[N];

struct ma {
	int n,m,a[25][25];
	ma() {
		n=m=0;
		memset(a,0,sizeof(a));
	}
	void clear() {
		n=m=0;
		memset(a,0,sizeof(a));
	}
} fir,sec;

void mul(ma &a,ma b) {
	ma re;
	int i,j,k;
	re.n=a.n;
	re.m=b.m;
	for(i=0; i<=re.n; i++)
		for(k=0; k<=a.m; k++) {
			if(!a.a[i][k])
				continue;
			for(j=0; j<=re.m; j++)
				re.a[i][j]=(re.a[i][j]+a.a[i][k]*b.a[k][j]%Mod)%Mod;
		}
	a=re;
}

void qpow(ma &x,ma &y,int t) {
	while(t) {
		if(t&1)
			mul(x,y);
		mul(y,y);
		t>>=1;
	}
}

int main() {
	scanf("%d%d%d",&m,&n,&Mod);
	scanf("%s",s);
	for(int i=0; i<n; i++)
		a[i]=s[i]-'0';
	a[n]=oo;
	wor[0]=wor[1]=0;
	int j=0;
	for(int i=1; i<n; i++) {
		while(j&&(a[i]!=a[j]))
			j=wor[j];
		j+=(a[i]==a[j]);
		wor[i+1]=j;
	}
	int k;
	for(int i=0; i<n; i++)
		for(int j=0; j<10; j++) {
			k=i;
			while(k&&a[k]!=j)
				k=wor[k];
			k+=(a[k]==j);
			if(k<n)
				sec.a[i][k]+=1;
		}
	sec.m=sec.n=fir.m=n-1;
	fir.n=0;
	fir.a[0][0]=1;
	qpow(fir,sec,m);
	for(int i=0; i<n; i++) {
		ans+=fir.a[0][i];
		ans%=Mod;
	}
	printf("%d\n",ans);
	return 0;
}