P4777 【模板】扩展中国剩余定理（EXCRT）

题目描述

给定 n 组非负整数 ai,b，求解关于 x 的方程组的最小非负整数解。​

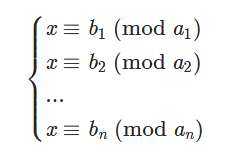
输入格式

输入第一行包含整数 n。

接下来 n 行，每行两个非负整数 ai,bi。

输出格式

输出一行，为满足条件的最小非负整数 x。

输入输出样例

输入 #1

3
11 6
25 9
33 17

输出 #1

809

说明/提示

n≤10^5,1≤ai≤10^12,0≤bi≤10^12,bi<ai，保证答案不超过10^18。

请注意程序运行过程中进行乘法运算时结果可能有溢出的风险。

数据保证有解

科普：EXCRT

巨佬的思路

代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N=100010;

int n;
long long aa[N],bb[N];

long long ksc(long long a,long long b,long long mod) {
	long long res=0;
	while(b>0) {
		if(b&1)
			res=(res+a)%mod;
		a=(a+a)%mod;
		b>>=1;
	}
	return res;
}

long long exgcd(long long a,long long b,long long &x,long long &y) {
	if(b==0) {
		x=1;
		y=0;
		return a;
	}
	long long gcd=exgcd(b,a%b,x,y);
	long long tp=x;
	x=y;
	y=tp-a/b*y;
	return gcd;
}

long long work() {
	long long x,y,k;
	long long M=bb[1],ans=aa[1];
	for(int i=2; i<=n; i++) {
		long long a=M,b=bb[i],c=((aa[i]-ans)%b+b)%b;
		long long gcd=exgcd(a,b,x,y),bg=b/gcd;
		if(c%gcd!=0)
			return -1;
		x=ksc(x,c/gcd,bg);
		ans+=x*M;
		M*=bg;
		ans=(ans%M+M)%M;
	}
	return (ans%M+M)%M;
}

int main () {
	freopen("excrt.in","r",stdin);
	freopen("excrt.out","w",stdout);
	scanf("%d",&n);
	for(int i=1; i<=n; i++) {
		scanf("%lld",&bb[i]);
		scanf("%lld",&aa[i]);
	}
	printf("%lld\n",work());
	return 0;
}