P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入样例：

5 5

1 5 4 2 3

2 2 4

1 2 3 2

2 3 4

1 1 5 1

2 1 4

输出样例：

11

8

20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

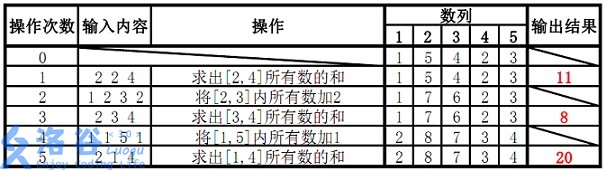
代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int N=1000010;;

long long n,m,a[N];
long long ans[N<<2],tag[N<<2];

void pushup(long long p) {
    ans[p]=ans[p<<1]+ans[p<<1|1];
}

void build(long long p,long long l,long long r) {
    tag[p]=0;
    if(l==r) {
        ans[p]=a[l];
        return ;
    }
    long long mid=(l+r)>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
    pushup(p);
}

void f(long long p,long long l,long long r,long long k) {
    tag[p]=tag[p]+k;
    ans[p]=ans[p]+k*(r-l+1);
}

void pushdown(long long p,long long l,long long r) {
    long long mid=(l+r)>>1;
    f(p<<1,l,mid,tag[p]);
    f(p<<1|1,mid+1,r,tag[p]);
    tag[p]=0;
}

void update(long long rt,long long nr,long long l,long long r,long long p,long long k) {
    if(rt<=l&&r<=nr) {
        ans[p]+=k*(r-l+1);
        tag[p]+=k;
        return ;
    }
    pushdown(p,l,r);
    long long mid=(l+r)>>1;
    if(rt<=mid)
        update(rt,nr,l,mid,p<<1,k);
    if(nr>mid)
        update(rt,nr,mid+1,r,p<<1|1,k);
    pushup(p);
}

long long query(long long x,long long y,long long l,long long r,long long p) {
    long long res=0;
    if(x<=l&&r<=y)
        return ans[p];
    long long mid=(l+r)>>1;
    pushdown(p,l,r);
    if(x<=mid)
        res+=query(x,y,l,mid,p<<1);
    if(y>mid)
        res+=query(x,y,mid+1,r,p<<1|1);
    return res;
}

int main() {
    long long a1,b,c,d,e,f;
    scanf("%lld%lld",&n,&m);
    for(long long i=1; i<=n; i++)
        scanf("%lld",&a[i]);
    build(1,1,n);
    while(m--) {
        scanf("%lld",&a1);
        if(a1==1) {
            scanf("%lld%lld%lld",&b,&c,&d);
            update(b,c,1,n,1,d);
        }
        if(a1==2) {
            scanf("%lld%lld",&e,&f);
            printf("%lld\n",query(e,f,1,n,1));
        }
    }
    return 0;
}

 

线段树2：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
//题目中给的p
int p;
//暂存数列的数组
long long a[100007];
//线段树结构体，v表示此时的答案，mul表示乘法意义上的lazytag，add是加法意义上的
struct node{
    long long v, mul, add;
}st[400007];
//buildtree
void bt(int root, int l, int r){
//初始化lazytag
    st[root].mul=1;
    st[root].add=0;
    if(l==r){
        st[root].v=a[l];
    }
    else{
        int m=(l+r)/2;
        bt(root*2, l, m);
        bt(root*2+1, m+1, r);
        st[root].v=st[root*2].v+st[root*2+1].v;
    }
    st[root].v%=p;
    return ;
}
//核心代码，维护lazytag
void pushdown(int root, int l, int r){
    int m=(l+r)/2;
//根据我们规定的优先度，儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag
    st[root*2].v=(st[root*2].v*st[root].mul+st[root].add*(m-l+1))%p;
    st[root*2+1].v=(st[root*2+1].v*st[root].mul+st[root].add*(r-m))%p;
//很好维护的lazytag
    st[root*2].mul=(st[root*2].mul*st[root].mul)%p;
    st[root*2+1].mul=(st[root*2+1].mul*st[root].mul)%p;
    st[root*2].add=(st[root*2].add*st[root].mul+st[root].add)%p;
    st[root*2+1].add=(st[root*2+1].add*st[root].mul+st[root].add)%p;
//把父节点的值初始化
    st[root].mul=1;
    st[root].add=0;
    return ;
}
//update1，乘法，stdl此刻区间的左边，stdr此刻区间的右边，l给出的左边，r给出的右边
void ud1(int root, int stdl, int stdr, int l, int r, long long k){
//假如本区间和给出的区间没有交集
    if(r<stdl || stdr<l){
        return ;
    }
//假如给出的区间包含本区间
    if(l<=stdl && stdr<=r){
        st[root].v=(st[root].v*k)%p;
        st[root].mul=(st[root].mul*k)%p;
        st[root].add=(st[root].add*k)%p;
        return ;
    }
//假如给出的区间和本区间有交集，但是也有不交叉的部分
//先传递lazytag
    pushdown(root, stdl, stdr);
    int m=(stdl+stdr)/2;
    ud1(root*2, stdl, m, l, r, k);
    ud1(root*2+1, m+1, stdr, l, r, k);
    st[root].v=(st[root*2].v+st[root*2+1].v)%p;
    return ;
}
//update2，加法，和乘法同理
void ud2(int root, int stdl, int stdr, int l, int r, long long k){
    if(r<stdl || stdr<l){
        return ;
    }
    if(l<=stdl && stdr<=r){
        st[root].add=(st[root].add+k)%p;
        st[root].v=(st[root].v+k*(stdr-stdl+1))%p;
        return ;
    }
    pushdown(root, stdl, stdr);
    int m=(stdl+stdr)/2;
    ud2(root*2, stdl, m, l, r, k);
    ud2(root*2+1, m+1, stdr, l, r, k);
    st[root].v=(st[root*2].v+st[root*2+1].v)%p;
    return ;
}
//访问，和update一样
long long query(int root, int stdl, int stdr, int l, int r){
    if(r<stdl || stdr<l){
        return 0;
    }
    if(l<=stdl && stdr<=r){
        return st[root].v;
    }
    pushdown(root, stdl, stdr);
    int m=(stdl+stdr)/2;
    return (query(root*2, stdl, m, l, r)+query(root*2+1, m+1, stdr, l, r))%p;
}
int main(){
    int n, m;
    scanf("%d%d%d", &n, &m, &p);
    for(int i=1; i<=n; i++){
        scanf("%lld", &a[i]);
    }
    bt(1, 1, n);
    while(m--){
        int chk;
        scanf("%d", &chk);
        int x, y;
        long long k;
        if(chk==1){
            scanf("%d%d%lld", &x, &y, &k);
            ud1(1, 1, n, x, y, k);
        }
        else if(chk==2){
            scanf("%d%d%lld", &x, &y, &k);
            ud2(1, 1, n, x, y, k);
        }
        else{
            scanf("%d%d", &x, &y);
            printf("%lld\n", query(1, 1, n, x, y));
        }
    }
    return 0;
}