b+树的索引数据在磁盘中的查找过程
B树
我们来介绍面向磁盘结构一种最长见的数据结构 -- B树。他应该是大家在日常接触最多的数据结构之一了~ 因为只要你在使用数据库,你就是在用B树。甚至当你在用hbase的时候,他其实也只是个分布式的大B树而已。
我们一直都在强调,硬件是骨头,软件是肉。软件的目标就是尽可能的发挥硬件的技术特性,并尽可能的绕开硬件的限制。
那么,作为骨头的磁盘,具有什么样的硬件特性呢?
在之前的文章中,我们已经给大家介绍过了磁盘的一些具体的技术特性,下面我们用一句话概括一下,如果要发挥磁盘的全部特性,软件需要满足的技术特点:一次读取或写入固定大小的一块数据,并尽可能减少随机查找这个操作的次数(因为随机查找意味着随机寻道)。嗯 我是特意没有写顺序读写这个操作的,因为我认为,只要能做到上面两个条件,那么顺序读写就能够自然而然的做到。
而对于ssd来说,如果要发挥ssd的全部特性,那么软件需要满足的技术特点是:一次读取或写入固定大小的一块数据,并尽可能的减少删除这个操作的次数(因为ssd的擦除操作需要的代价比较大)
通过上面的两个介绍,你一定会发现,无论ssd还是磁盘,他们都有一个共性的要求是,一次读写固定大小的一块数据。
不知道这时候大家会不会立刻联想到一个数据结构?对,就是数组。 数组的特性就是拥有固定的大小。
但是,回忆一下之前我们说过的: 有序数组有一个最大的难点就在于如何能够让数组以更便宜的方式来实现数组的自动扩展。
好,铺垫了这么多,我们终于要开始进入正题了~
因为数组的大小是固定的,那么如果想扩展怎么办呢?
一种能够想到的方式是,每次满了就创建一个新数组,然后数据全复制到新数组中 。但这样做有个很大的问题,是每一次都需要做一次数据的全拷贝,代价相对比较大。
另外一种方式是,保持数组大小不变,但增加数组的个数,不是也可以增加整个数据结构承载数据的总量么?
这个思路就是b树的核心思路,另外这里有个小八卦要给大家说一下,大家经常看到的b树,b-树,其实是同一类结构,b-树不是“b减树”的意思哦~
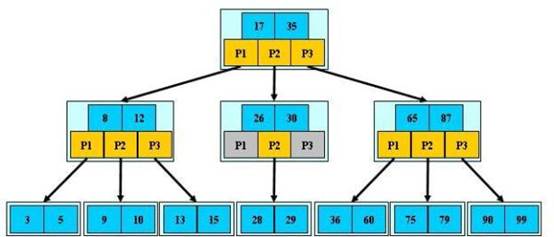
那么b树的核心是几个关键词
1. 树高:一般来说,树的高度要比二叉平衡树低很多
2. 数组:每一个node,都是一个“数组”,数组是很关键的决定性因素,我们后面写入和读取分析的时候会讲到。
然后我们进行一下读取和写入的模拟。
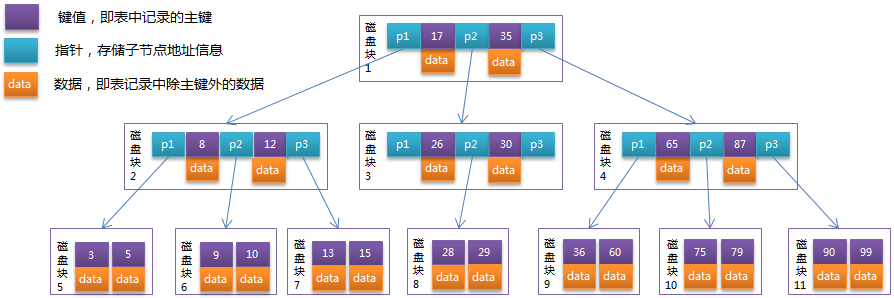
从读取来说:如果我要查找28这个数据对应的value是多少,路径大概是:首先走root节点,取出root node后,对该数组进行二分查找,发现35>28>17,所以进入branch节点中的第二个节点,取出该节点后再进行二分查找。发现30>28>26,所以进入branch节点的p2 value,取出该节点,对该三个值的数组进行二分查找,从而定位到28这个数据的对应value。
而写入删除则涉及到分裂和合并这两个btree最重要的操作,比如,要写入37,那么会先找到36所应该被插入的数组[36,60]这个数组,然后判断其是否有空,如果有空,则对该数组进行重新排序。而如果没有空,则必须要进行分裂。分裂的缘由是因为组成b-tree的每一个node,都是一个数组,数组最大的特性是,数组内元素个数是固定的。因此必须要把原有已经满掉的数组里面的一半的数据拿出来,放到新的一个新建立的空数组中,然后把要写入的数据写入到老或新的这两个数组里面的一个里面去。
【这里要留个问题给大家了,我想问一下,为什么b-tree要使用数组来存储数据呢?为什么不选择链表等结构呢?】
对于上面的这个小的b-tree sample里面呢,因为数组[35,60],数组已经满了,所以要进行分裂。于是数组在插入了新值以后,变成了两个[35,36] 和[60] ,然后再改变父节点的指针并依次传导上去即可。
当出现删除的时候,会可能需要进行合并的工作,也就是写入这个操作的反向过程。在一些场景中,因为不断地插入新的id,删除老的id,会造成b-tree的右倾,这时候需要有后台进程对这种倾向进行不断地调整。
基本上,这就是b-tree的运转过程了。
B+tree
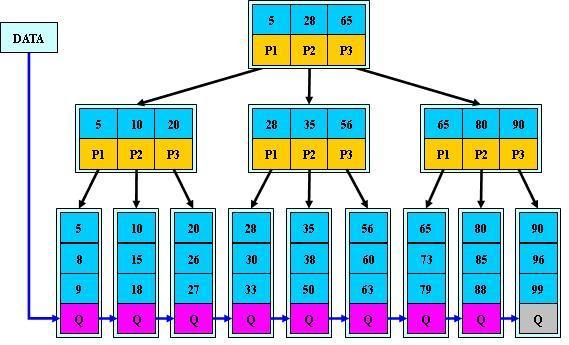
B+tree 其实就是在原有b-tree的基础上。增加两条新的规则
1. Branch节点不能直接查到数据后返回,所有数据必须读穿或写穿到leaf节点后才能返回成功
2. 子叶节点的最后一个元素是到下一个leaf节点的指针。
这样做的原因是,更方便做范围查询,在b+树种,如果要查询20~56.只需要找到20这个起始节点,然后顺序遍历,不再需要不断重复的访问branch和root节点了。
在了解了b树的基本原理了以后,让我们来做一个小结。
在面向磁盘/ssd的数据结构中,因为从这类介质中进行查找和写入的代价远远的大于内存,并且一次必须读取一个或几个相邻块内的数据效率才会高,而随机寻道次数则直接决定了磁盘的瓶颈。因此,面向磁盘类的结构一个最重要的理念,就是尽可能的减少磁盘寻道次数。而实现这个理念所依托的核心思路,就是让每一个取出的块都能拥有更大的价值。举个例子,如果磁盘进行了一次随机寻道,拿到了一批数据,而这个批内可以进行4次二分查找。那么如果要从2^8个数据内定位到我们所需要的数据,则只需要进行两次随机寻道,取出两批数据,就可以定位到数据了。
这是针对这类整块取出或写入数据的硬件的一种通用的解决方法,后面我们介绍的其他面向磁盘的数据结构,也都拥有类似的结构,而不同点则主要是针对一些具体的硬件技术特性而做出的针对性的优化。这个到我们介绍LSM/SSTable的时候大家就会看到。
B树是上世纪80年代的产物,设计上是比较简单的,因为b树采取的是原位更新的方式,所以对读取是比较优化的,而代价是在写入的时候也需要先通过随机查找来找到数据要写入的目标位置,这个操作会导致磁盘的随机写。因此对写入而言,如果你使用的是磁盘,那么很可能在不断地写入删除写入删除多次后,b树会出现更多的随机寻道,从而导致写的性能下降。
B树另外的一个挑战则是如何保持b树元素的均衡,如果各位实际的观察过数据库,都会发现随着用户的使用,数据库可能都会出现一定程度的向右的倾斜,这种现象产生的主要原因与我们使用b树的方式有一定关系,因为我们往往会给数据增加一个唯一标识,写入的时候则主要会以单调递增的方式创建这个id。那么最后我们写入数据库的一个数据的序列就可能是:插入1,2,3,删除3,插入4,5,7 ,删除4,5 插入8,9,10。。。一直这样写入下去,就会出现前面的节点数据相对的比较松散,而后面的数据则相对的比较致密,虽然前面的数据比较松散,但松散却并不意味着空间节省,因为b树必须保证全局有序,因此空间只能被空在那里,造成了较多的空间浪费。这个问题主要的解决方法就是做一个后台线程,不断的将前面的数据做一个数据整理,并写到新的块内。以腾出更多的空间。
下面照例,我们使用一些通用的标准对b树进行一下简单的评价:
1.是否支持范围查找
因为是有序结构,所以能够很好的支持范围查找。
2.集合是否能够随着数据的增长而自动扩展
可以,主要增长方式如下: 如果单个数组内还有空隙,那么数据可以直接放入数组内,而如果数组没有空隙,则进行分裂,从而可以支持数据的自动扩展。
3.读写性能如何
因为从宏观上可以做到一次排除一半的数据,并且在写入时也没有进行其他额外的数据查找性工作,所以对于b树来说,其读写的时间复杂度都是O(log2n)。
4.是否面向磁盘结构
一般来说,在有内存的情况下,root层和branch里面的一部分都会被缓存在内存中,所以如果树的高度是三层,那么前两层一般都会被缓存在内存中,所以查询基本上只需要一次随机寻道时间, 这比二叉树系列和skiplist系列都要强不少。
5.并行指标
b树也是一个并行度比较不错的数据结构,相比较skiplist而言,他很难使用compare and set的方式来进行数据的写入,而必须使用lock来保证读写访问的同步。不过因为可以尽可能的将锁下推,所以锁的颗粒度可以维持在比较小的级别,从而可以提供比较高的并行度。同时,因为b树主要使用的目标场景是磁盘,对于磁盘读写来说,Compare and set 带来的性能提升几乎可以忽略。因此我们可以认为,b树的并行度比skiplist要差,但比其他树的要好
6.内存占用
这是b树的一个短板,在最坏的情况下,b树的所有块都刚好做完分裂。那么整棵树需要消耗两倍的空间才能存储下所有的数据,空间相对的有些浪费。所以一般会通过重新平衡的方式加以部分的纠正





 浙公网安备 33010602011771号
浙公网安备 33010602011771号