二分查找算法(递归)
二分查找算法
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
你观察这个列表,这是不是一个从小到大排序的有序列表呀?
如果这样,假如我要找的数比列表中间的数还大,是不是我直接在列表的后半边找就行了?
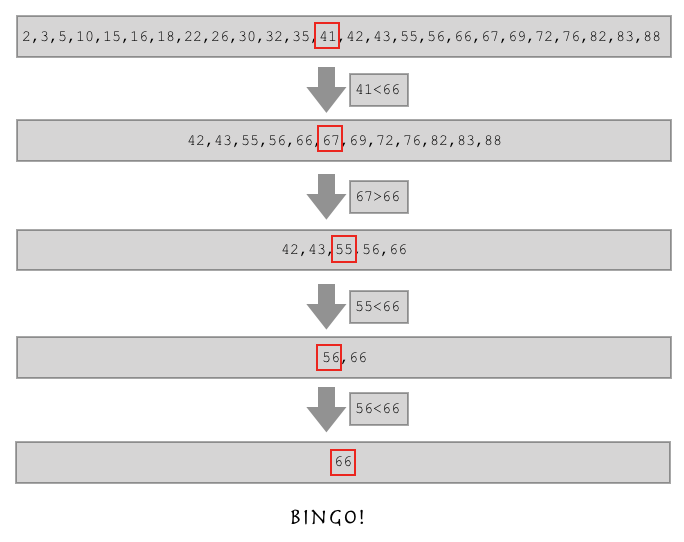
这就是二分查找算法!
那么落实到代码上我们应该怎么实现呢?
简单版二分法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
def func(l,aim):
mid = (len(l)-1)//2
if l:
if aim > l[mid]:
func(l[mid+1:],aim)
elif aim < l[mid]:
func(l[:mid],aim)
elif aim == l[mid]:
print("bingo",mid)
else:
print('找不到')
func(l,66)
func(l,6)
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
def func(l,aim):
mid = (len(l)-1)//2
if l:
if aim > l[mid]:
func(l[mid+1:],aim)
elif aim < l[mid]:
func(l[:mid],aim)
elif aim == l[mid]:
print("bingo",mid)
else:
print('找不到')
func(l,66)
func(l,6)
升级版二分法

def search(num,l,start=None,end=None):
start = start if start else 0
end = end if end is None else len(l) - 1
mid = (end - start)//2 + start
if start > end:
return None
elif l[mid] > num :
return search(num,l,start,mid-1)
elif l[mid] < num:
return search(num,l,mid+1,end)
elif l[mid] == num:
return mid
def search(num,l,start=None,end=None):
start = start if start else 0
end = end if end is None else len(l) - 1
mid = (end - start)//2 + start
if start > end:
return None
elif l[mid] > num :
return search(num,l,start,mid-1)
elif l[mid] < num:
return search(num,l,mid+1,end)
elif l[mid] == num:
return mid
# 什么叫算法
# 计算的方法 : 人脑复杂 计算机简单
# 99 * 13 = 1287 = 13*100 - 13
# 查找 : 找数据
# 排序 :
# 最短路径
# 我们学习的算法 都是过去时
# 了解基础的算法 才能创造出更好的算法
# 不是所有的事情都能套用现成的方法解决的
# 有些时候会用到学过的算法知识来解决新的问题
# 二分查找算法 必须处理有序的列表
# l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
# 5000000 4999998
# 代码实现
# def find(l,aim):
# mid_index = len(l) // 2
# if l[mid_index] < aim:
# new_l = l[mid_index+1 :]
# find(new_l,aim)
# elif l[mid_index] > aim:
# new_l = l[:mid_index]
# find(new_l, aim)
# else:
# print('找到了',mid_index,l[mid_index])
#
# find(l,66)
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
# def find(l,aim,start = 0,end = None):
# end = len(l) if end is None else end # end = len(l) 24
# mid_index = (end - start)//2 + start #计算中间值 12 + 0 = 12
# if l[mid_index] < aim: #l[12] < 44 #41 < 44
# find(l,aim,start =mid_index+1,end=end) # find(l,44,start=13,end=24)
# elif l[mid_index] > aim:
# find(l, aim, start=start, end=mid_index-1)
# else:
# print('找到了',mid_index,aim)
#
# def find(l,aim,start = 0,end = None): # l,44,start=13,end=24
# end = len(l) if end is None else end # end = 24
# mid_index = (end - start)//2 + start #计算中间值 24-13/2 = 5 + 13 = 18
# if l[mid_index] < aim: #l[18] < 44 #67 < 44
# find(l,aim,start =mid_index+1,end=end)
# elif l[mid_index] > aim: # 67 > 44
# find(l, aim, start=start, end=mid_index-1) # find(l,44,start=13,end=17)
# else:
# print('找到了',mid_index,aim)
#
# def find(l,aim,start = 0,end = None): # l,44,start=13,end=17
# end = len(l) if end is None else end # end = 17
# mid_index = (end - start)//2 + start #计算中间值 17-13/2 = 2 + 13 = 15
# if l[mid_index] < aim: #l[15] < 44 #55 < 44
# find(l,aim,start =mid_index+1,end=end)
# elif l[mid_index] > aim: # 55 > 44
# find(l, aim, start=start, end=mid_index-1) # find(l,44,start=13,end=14)
# else:
# print('找到了',mid_index,aim)
#
# def find(l,aim,start = 0,end = None): # l,44,start=13,end=14
# end = len(l) if end is None else end # end = 14
# mid_index = (end - start)//2 + start #计算中间值 14-13/2 = 0+ 13 = 13
# if l[mid_index] < aim: #l[13] < 44 #42 < 44
# find(l,aim,start =mid_index+1,end=end) # find(l,44,start=14,end=14)
# elif l[mid_index] > aim: # 42 > 44
# find(l, aim, start=start, end=mid_index-1)
# else:
# print('找到了',mid_index,aim)
def find(l,aim,start = 0,end = None):
end = len(l) if end is None else end
mid_index = (end - start)//2 + start
if start <= end:
if l[mid_index] < aim:
return find(l,aim,start =mid_index+1,end=end)
elif l[mid_index] > aim:
return find(l, aim, start=start, end=mid_index-1)
else:
return mid_index
else:
return '找不到这个值'
ret= find(l,44)
print(ret)
# 参数 end
# 返回值
# 找不到的话怎么办
# l.index()
# 67 发生两次调用
# 66 发生好几次
# 44 找不到
# age,二分查找,三级菜单的代码看一遍
# 斐波那契 # 问第n个斐波那契数是多少
# 阶乘
#3! 3*2*1
# 附加题 :考试附加题
# 递归实现



 浙公网安备 33010602011771号
浙公网安备 33010602011771号