Codeforces Round #608 (Div. 2) E. Common Number

题目链接：https://codeforces.com/contest/1271/problem/E

题意：给定函数f(x)，x为偶数时f(x)=x/2，x为奇数时f(x)=x-1

给定n，k，对1到n每个数求f(x)的轨迹，如path[15]={15，14，7，6，3，2，1}，求在所有轨迹里出现次数大于等于k的最大值ans。

 

以下为轨迹图：n=31时，4在4-5、8-11、16-23中都出现了

n的大小只能控制最后一层的数目

 

 

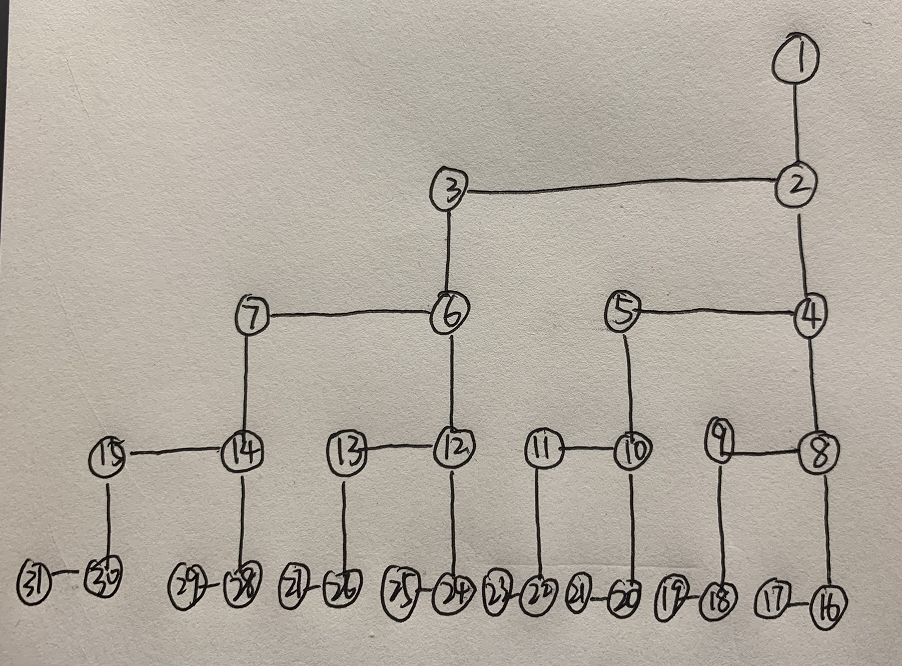
当图最后一层完整时，每一层的奇数、偶数出现的次数都相等

当图最后一层不完整时，每一层较右（较小）的偶数出现次数总是大于较左的偶数出现次数，奇数同理

所以把奇偶分开来，奇数列和偶数列都呈单调递减态，可以用二分来判断

求出出现次数大于等于k的最大奇数、最大偶数，再求max

 

如何求某个数的出现次数？

4的次数=(5-4+1)+(11-8+1)+(23-16+1)，16为不超过n的最大2的次方，23=11*2+1，11=5*2+1

需要注意最后一层不一定完整，23、11等只是个理论值，可能会超过n，当其超过n时要取n

参考自：https://www.cnblogs.com/Herlo/p/12082724.html

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,k;
bool check(ll tmp)
{
    queue<pair<ll,ll> >q;
    if(tmp&1)q.push(make_pair(tmp,tmp));
    else q.push(make_pair(tmp,tmp+1));
    ll ans=0;
    while(q.size())
    {
        auto it=q.front();
        q.pop();
        ans+=min(n,it.second)-it.first+1;
        if((it.first<<1)<=n)q.push(make_pair(it.first<<1,it.second<<1|1));
    }
    return ans>=k;
}
int main()
{
    ll ans=0;
    cin>>n>>k;
    
    ll l=0,r=n/2;
    while(l<=r)
    {
        ll mid=l+r>>1;
        if(check(mid<<1|1))
        {
            ans=max(ans,mid<<1|1);
            l=mid+1;
        }
        else r=mid-1;
    }
    
    l=1,r=n/2;//偶数枚举只能枚因子 
    while(l<=r)
    {
        ll mid=l+r>>1;
        if(check(mid<<1))
        {
            ans=max(ans,mid<<1);
            l=mid+1;
        }
        else r=mid-1;
    }
    cout<<ans<<endl;
    return 0;
} 

 

进阶解法：

尚未参透

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll solve(ll n,ll k)
{
    ll tmp=1;
    while(tmp<=k)tmp*=2;
    tmp/=2;
    //return (n-k+tmp)/tmp; 
    return 1+(n-k)/tmp;
}
int main()
{
    ll n,k,ans;
    cin>>n>>k; 
    ans=max(solve(n,k),solve(n,k+1)<<1);
    cout<<ans<<endl;
    return 0;
}