Codeforces Round #609 (Div. 2)
题目链接：http://codeforces.com/contest/1269
给定n，找到任意两个1e9范围内的a和b，满足a-b=n，a和b都不是质数
#include<bits/stdc++.h> using namespace std; const int mod=1e9+7; int main() { int n; cin>>n; if(n%2==0)cout<<4+n<<" "<<4<<endl; else cout<<9+n<<" "<<9<<endl; return 0; }
给定n，m，长度为n的数组a，长度为n的数组b
所有a[i]加上x后再对m取余，使得a[i]与b[i]相等（与顺序无关），保证有解，输出最小的非负x
将两个数组a合并，后面一个数组a每个数加上m，a数组的差(len=n*2-1)和b数组的差(len=n-1)做kmp
#include<bits/stdc++.h> using namespace std; const int mod=1e9+7; const int maxn=5e3+10; int a[maxn],pre[maxn],b[maxn],pre2[maxn],n,m; int Next[maxn]; void get_Next() { for(int i=1;i<n-1;i++) { int j=Next[i]; while(j&&pre2[i]!=pre2[j])j=Next[j]; Next[i+1]=pre2[i]==pre2[j]?j+1:0; } } int kmp() { get_Next(); int j=0; for(int i=0;i<2*n-1;i++) { while(j&&pre[i]!=pre2[j])j=Next[j]; if(pre[i]==pre2[j])j++; if(j==n-1)return i-(n-1)+1; } return -1; } int main() { cin>>n>>m; for(int i=0;i<n;i++)cin>>a[i]; for(int i=0;i<n;i++)cin>>b[i]; sort(a,a+n); sort(b,b+n); for(int i=n;i<2*n;i++)a[i]=a[i-n]+m; for(int i=1;i<2*n;i++)pre[i-1]=a[i]-a[i-1]; for(int i=1;i<n;i++)pre2[i-1]=b[i]-b[i-1]; int ans=kmp(); cout<<(b[0]+m-a[ans]+m)%m<<endl;//两个m return 0; }
给定n，k，字符串s
要求构造一个循环节长度为k的字符串str，使得str（作为数字来比）大于等于s，输出最小的str以及str的长度
假设str全是9，必大于等于s，所以长度固定为n
先判断s前k个构成的循环节是否大于等于，是则直接输出
否则把循环节的末尾加一，这个结果必符合，但是得考虑进位的情况
#include<bits/stdc++.h> using namespace std; const int maxn=2e5+10; int n,k; string s; string make(string tmp) { int len1=s.size(),len2=k; string s2=""; while(1) { s2+=tmp; if(len2+k>n) { s2+=tmp.substr(0,n-len2); break; } else len2+=k; } return s2; } string add(string tmp) { reverse(tmp.begin(),tmp.end()); int size=tmp.size(),flag=0; tmp[0]++; for(int i=0;i<size;i++) { if(tmp[i]>'9') { if(i==size-1)flag=1; tmp[i+1]++,tmp[i]=(tmp[i]-'0')%10+'0'; } } reverse(tmp.begin(),tmp.end()); if(flag==1)return "1"+tmp; return tmp; } int main() { ios::sync_with_stdio(0); cin>>n>>k; cin>>s; string tmp=s.substr(0,k); string ans=make(tmp); if(ans<s) { tmp=add(tmp); ans=make(tmp); } cout<<ans.size()<<endl; cout<<ans<<endl; return 0; }
给定n，给定长度为n的数组a，a[i]表示第i列的正方块的数量，i和a[i]都不大于3e5（掐指一算，遍历不行）
用1×2或者2×1的长方块填满图像，问最多能用几个
个人对min(x,y)的理解：
i为奇的奇数列和i为偶的奇数列，
占地（偶+2）*奇，必可以被1*2或2*1填满
横方向差偶数块，纵方向差偶数块，也可以填满
中间是偶*偶，也可以填满(递归来思考)
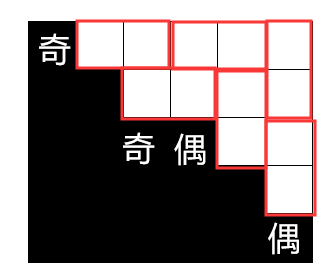
#include<bits/stdc++.h> using namespace std; int main() { long long res=0,x=0,y=0,n,m; scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&m); res+=m/2; if(m&1) { if(i&1)x++; else y++; } } res+=min(x,y); printf("%lld\n",res); return 0; }
不补
