线段树+lazy标记 2019年8月10日计蒜客联盟周赛 C.小A的题

题目链接：https://nanti.jisuanke.com/t/40852

题意：给定一个01串s，进行m次操作，|s|<=1e6，m<=5e5

操作有两种

l r 0，区间[l,r]升序排序

l r 1，区间[l,r]降序排序

输出m次操作后的串s

 

官方解析：

维护区间1的个数，区间0的个数=区间长度-区间1的个数，完成区间赋值操作并更新即可。

 

个人思路：

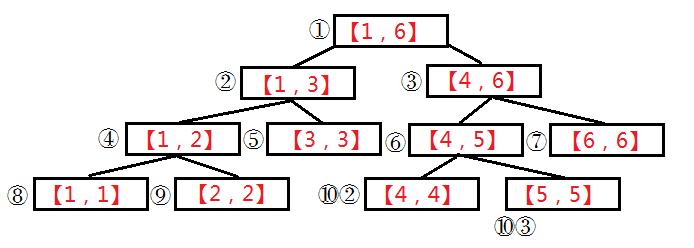
线段树的操作都是log(n)，如果带了lazy标记，就可以小于log(n)，不必查询到每个点。例如将[1,3]都置为1，只用将t[2]=3即可。

另外tag是标记升序降序的lazy标记，在update和getsum中会进行标记下放。

时间复杂度小于O（m*log(|S|)）

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const int maxl=1e6+5;
const int manx=5e5+5;
char s[maxl];
int t[maxl*4],tag[maxl*4];
inline int read()
{
    int f=1,x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    return x*f;
}

void build(int x,int l,int r)//t[x]记录1的个数 
{
    tag[x]=-1;
    if(l==r)
    {
        t[x]=s[l]-'0';
        return;
    }
    int mid=(l+r)/2;
    build(x*2,l,mid);
    build(x*2+1,mid+1,r);
    t[x]=t[x*2]+t[x*2+1]; //x<<1|1
}
int getsum(int x,int l,int r,int L,int R)  //L R是要求的sum区间 
{
    if(l==L&&r==R)return t[x];
    int mid=(l+r)/2;
    if(tag[x]!=-1)
    {
        tag[x*2]=tag[x*2+1]=tag[x];
        t[x*2]=tag[x]?(mid-l+1):0;
        t[x*2+1]=tag[x]?(r-mid):0;
        tag[x]=-1;
    } 
    if(R<=mid)return getsum(x*2,l,mid,L,R);
    else if(L>mid)return getsum(x*2+1,mid+1,r,L,R);
    else return getsum(x*2,l,mid,L,mid)+getsum(x*2+1,mid+1,r,mid+1,R); 
} 
void update(int x,int l,int r,int L,int R,int v)
{
    if(l==L&&r==R)
    {
        tag[x]=v;
        t[x]=v?(r-l+1):0;
        return;
    }
    int mid=(l+r)/2;
    if(tag[x]!=-1)
    {
        tag[x*2]=tag[x*2+1]=tag[x];
        t[x*2]=tag[x]?(mid-l+1):0;
        t[x*2+1]=tag[x]?(r-mid):0;
        tag[x]=-1;
    }
    if(R<=mid) update(x*2,l,mid,L,R,v);
    else if(L>mid) update(x*2+1,mid+1,r,L,R,v);
    else 
    {
        update(x*2,l,mid,L,mid,v);
        update(x*2+1,mid+1,r,mid+1,R,v);
    }
    t[x]=t[x*2]+t[x*2+1];
}
void dfs(int x,int l,int r)
{
    if(l==r)
    {
        printf("%d",t[x]);
        return;
    }
    int mid=(l+r)/2;
    if(tag[x]!=-1)
    {
        tag[x*2]=tag[x*2+1]=tag[x];
        t[x*2]=tag[x]?(mid-l+1):0;
        t[x*2+1]=tag[x]?(r-mid):0;
        tag[x]=-1;
    }
    dfs(x*2,l,mid);
    dfs(x*2+1,mid+1,r);
}
int main()
{
    scanf("%s",s+1);
    int n=strlen(s+1);
    build(1,1,n);
    int m=read();
    int u,v,w;
    while(m--)
    {
        u=read();v=read();w=read();  //[u,v]，w=0升序，w=1降序 
        int sum=getsum(1,1,n,u,v);  //算出有几个1 
        if(sum==0||sum==(v-u+1))continue;
        if(w==0)update(1,1,n,u,v-sum,0),update(1,1,n,v-sum+1,v,1);
        else update(1,1,n,u,u+sum-1,1),update(1,1,n,u+sum,v,0);
    } 
    dfs(1,1,n);
    return 0;
} 

另：移位符号计算比*号快，线段树要开四倍空间