hdu 3572 Task Schedule(最大流)2010 ACM-ICPC Multi-University Training Contest(13)——Host by UESTC
题意:
告诉我们有m个任务和k个机器。第i个任务需要ci天完成,最早从第ai天开始,最晚在第bi天结束。每台机器每天可以执行一个任务。问,是否可以将所有的任务都按时完成?
输入:
首行输入一个整数t,表示共有t组数据。
接下来,每组数据第一行输入两个整数k,m,表示共有k项任务,m台机器。
接下来k行,每行包括三个整数ci,ai,bi。
输出:
如果可以完成所有任务,输出——Case i: Yes
否则,输出——Case t: No
注意,每组输出占2行
这道题我如何也想不到是个最大流。即使我知道这是最大流,我也想不出来如何建图。看了题解后,才恍然大悟。
题解:
首先建立一个超级源点0.
从1到k表示k项任务的节点,ki表示第i项任务。
从k+1到m+k表示机器的节点,第k+mi表示第mi台机器。
从m+k+1到m+k+l表示时间的节点。第m+k+li表示第li天。
最后一个超级汇点m+k+l+1。
然后从0到ki用ci连接——mp[0][ki] = ci; 表示第ki项任务需要执行ci天。
从ki到m+k+lj用1连接——mp[ki][m+k+lj] = 1; 表示第ki项任务在第lj天执行一天。
从m+k+lj到k+mi用1连接——mp[m+k+lj][k+mi] = 1; 表示第lj天使用了mi一天。
然后从k+mi到m+k+l+1用l连接——mp[k+mi][m+k+l+1] = l; 表示第mi台机器最多可以使用l天。
接下来将这张图进行运算。如果最大流等于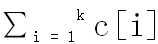 ,则可以完成。
,则可以完成。
同样使用Dinic算法。
上代码——

1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 using namespace std; 7 8 const int N = 2010; 9 const int M = 10000010; 10 11 int mp[N][N]; 12 int dis[N]; 13 int cur[N]; 14 bool vis[N]; 15 int t, k, m, n, l, ans, sum; 16 17 inline int Min(int x, int y) 18 { 19 return x < y ? x : y; 20 } 21 22 void init() //神奇的建图 23 { 24 scanf("%d%d", &k, &m); 25 l = 0; 26 sum = 0; 27 memset(mp, 0, sizeof(mp)); 28 for(int i = 1; i <= k; i++) 29 { 30 int a, b, c; 31 scanf("%d%d%d", &c, &a, &b); 32 if(l < b) l = b; 33 mp[0][i] = c; 34 sum += c; 35 for(int j = a; j <= b; j++) 36 { 37 mp[i][k+m+j] = 1; 38 } 39 } 40 n = k+m+l+1; 41 for(int i = 1; i <= m; i++) 42 { 43 for(int j = 1; j <= l; j++) mp[m+k+j][k+i] = 1; 44 mp[k+i][n] = l; 45 } 46 ans = 0; 47 } 48 49 bool bfs() 50 { 51 memset(vis, 0, sizeof(vis)); 52 queue<int> que; 53 que.push(0); 54 vis[0] = 1; 55 dis[0] = 0; 56 while(!que.empty()) 57 { 58 int k = que.front(); 59 que.pop(); 60 for(int i = 0; i <= n; i++) 61 { 62 if(!vis[i] && mp[k][i] > 0) 63 { 64 vis[i] = 1; 65 dis[i] = dis[k]+1; 66 que.push(i); 67 } 68 } 69 } 70 return vis[n]; 71 } 72 73 int dfs(int x, int val) 74 { 75 if(x == n || val == 0) return val; 76 int flow = 0, minn; 77 for(int& i = cur[x]; i <= n; i++) 78 { 79 if(dis[x]+1 == dis[i] && (minn = dfs(i, Min(val, mp[x][i]))) > 0) 80 { 81 mp[x][i] -= minn; 82 mp[i][x] += minn; 83 val -= minn; 84 flow += minn; 85 if(val == 0) break; 86 } 87 } 88 return flow; 89 } 90 91 void work() //开始搜图,即使用Dinic算法 92 { 93 while(bfs()) 94 { 95 for(int i = 0; i <= n; i++) cur[i] = 0; 96 ans += dfs(0, M); 97 } 98 } 99 100 void outit(int tm) 101 { 102 printf("Case %d: ", tm); 103 if(ans == sum) printf("Yes\n\n"); 104 else printf("No\n\n"); 105 } 106 107 int main() 108 { 109 //freopen("test.in", "r", stdin); 110 scanf("%d", &t); 111 for(int tm = 1; tm <= t; tm++) 112 { 113 init(); 114 work(); 115 outit(tm); 116 } 117 return 0; 118 }
只是别人使用15ms,我用300+ms。看来还是需要优化啊。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号