数据结构与算法 图论（三）最小生成树

Kruskal算法

对边排序，选出n-1条路径最短的边。即得到一个最小生成树。

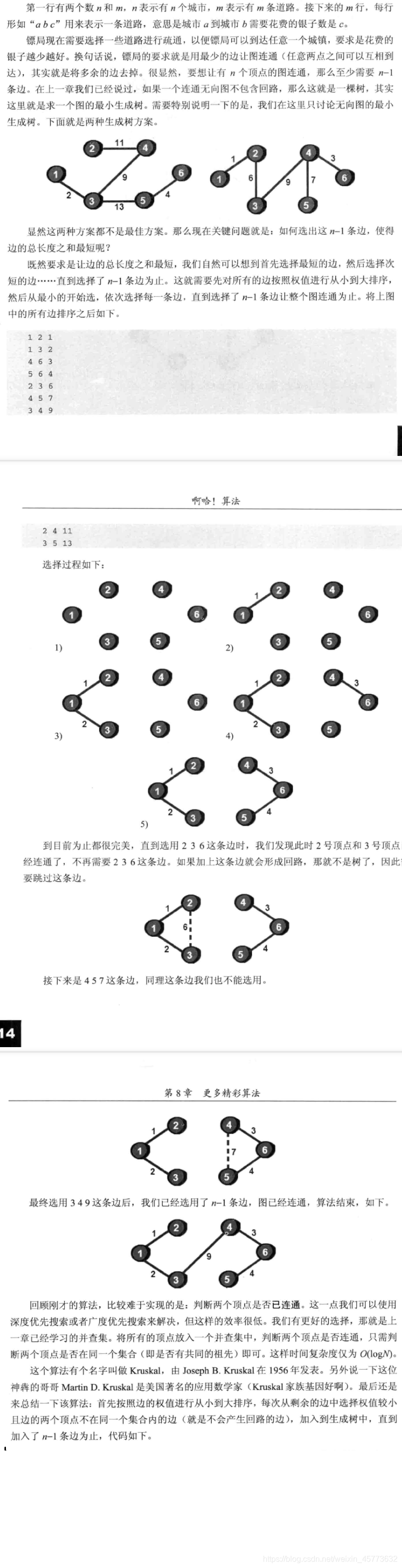
在选边过程中，需要判断，两点是否已经连通。可以使用dfs或bfs但是效率很低，这里使用并查集来判断图中的两点是否已经连通.。

import java.util.Scanner;

public class zuixiaoshengchengshu {
    static class edge{
        int u;
        int v;
        int w;
    }
    static edge [] e;
    static int [] f;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int count=0,sum=0;
        int n = scan.nextInt();
        int m = scan.nextInt();
        e = new edge[m+1];
        f = new int[n+1];
        for (int i = 1; i <= m; i++) {
            e[i] = new edge();
            e[i].u = scan.nextInt();
            e[i].v = scan.nextInt();
            e[i].w = scan.nextInt();
        }

        quickSort(1,m);
        init(n);

        for (int i = 1; i <= m; i++) {
            if (merge(e[i].u,e[i].v) != 0){
                count++;
                sum+=e[i].w;
            }
            if (count == n-1)
                break;
        }

        System.out.print(sum);
    }

    private static void quickSort(int left,int right) {
        int i,j,temp;
        edge t;
        if (left > right)   //'='的取舍
            return;
        temp = e[left].w;
        i = left;
        j = right;
        while (i != j){
            while (e[j].w >= temp && i < j)
                j--;
            while (e[i].w <= temp && i < j)
                i++;
            if (i < j){
                t = e[i];
                e[i] = e[j];
                e[j] = t;
            }
        }
        //基准数归位
        t = e[left];
        e[left] = e[i];
        e[i] = t;

        quickSort(left,i-1);
        quickSort(i+1,right);
    }

    //合并两子集的函数
    private static int merge(int v, int u) {
        int t1 = getf(v);
        int t2 = getf(u);
        if (t1 != t2){
            //靠左原则，左边变成右边的子集，即把右边的集合，作为左边集合的子集和
            f[t2] = t1;
            return 1;
        }
        return 0;
    }

    //找爹的函数，不停的去找爹，直到找到祖宗为止，其实就是找最高领导人
    private static int getf(int v){
        if (f[v] == v)
            return v;
        else {
            f[v]=getf(f[v]);
            return f[v];
        }
    }

    private static void init(int n) {
        for (int i = 1; i <= n; i++) {
            f[i] = i;
        }
    }

}

Prim算法

要用n-1条边将n个点连接起来，那么每个点都必须至少有一条边与它相连。

import java.util.Scanner;
public class Prim {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int [][] e = new int[7][7];
        int [] dis = new int[7];
        int [] book = new int[7];
        int inf = Integer.MAX_VALUE;
        int count=0,sum=0;
        int n = scan.nextInt();
        int m = scan.nextInt();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (i == j) e[i][j]=0;
                else e[i][j]=inf;
            }
        }

        for (int i = 1; i <= m; i++) {
            int t1 = scan.nextInt();
            int t2 = scan.nextInt();
            int t3 = scan.nextInt();
            e[t1][t2] = t3;
            e[t2][t1] = t3;
        }

        //初始化dis数组，这里是1号顶点到各个顶点的距离，因为当前是生成树中使用1号顶点
        for (int i = 1; i <= n; i++) {
            dis[i] = e[1][i];
        }

        //Prim核心
        book[1]=1;
        count++;
        while (count < n){
            int min = inf,j = 0;
            for (int i = 1; i <= n; i++) {
                if (book[i] == 0 && dis[i] < min){
                    min = dis[i];j=i;
                }
            }

            //为下一次找离生成树最近的点做准备
            book[j]=1;count++;sum+=dis[j];

            for (int i = 1; i <= n; i++) {
            //当点还没有加入生成树，就更新
                //注意：记录的是离生成树最近的点而不是离某一点最近的点，但是j只能最新加入到生成树中点。
                if (book[i] == 0 && dis[i] > e[j][i])
                    dis[i] = e[j][i];
            }
        }

        System.out.println(sum);
    }
}