深入理解KMP算法

 

KMP算法是一个从字符串A中查找字符串B的算法。

假设有字符串"ababababca",查找“abababca" ?

算法中定义一个部分匹配表（Partial Match Table，简称PMT）的数组，PMT就是是KMP算法的核心。

对于目标字符串“abababca" 的PMT如下图：

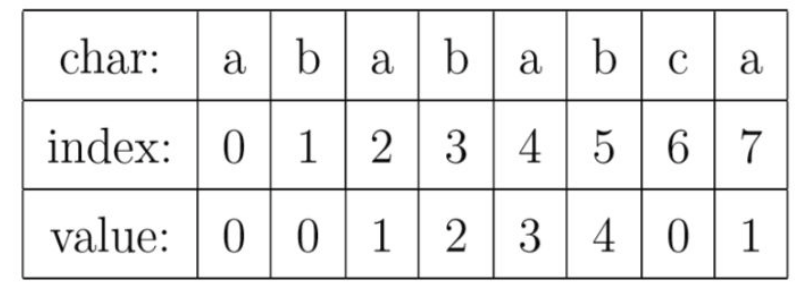
这里value,即pmt[index]的含义指的是字符串相同前缀后缀的最大长度。本文称这里的前缀和后缀为PMT前缀和PMT后缀。比如上图 index = 3时，此时字符串”abab"的前缀有{“a","ab","aba"},后缀有{”bab","ab","b"}，交集中长度最大的是“ab"，即此时PMT前缀和PMT后缀都是”ab",长度为2；

为了方便计算，对于PMT还定义了next值,具体定义是：当index = 0 ,next[index] = -1;当index >0 ,next[j] = pmt[j-1]; next[0]=-1的巧妙之处在代码中有解释；

如下图：

 

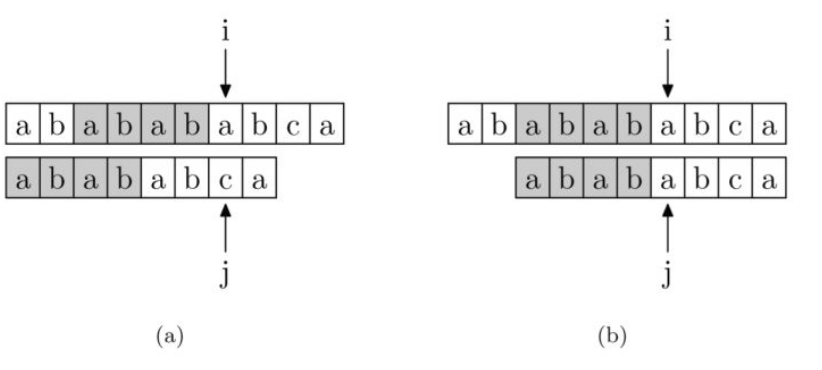
现在开始进行匹配，i和j分别前文说的字符串A和B中下标，下图a中，i和j指向字符串A和B刚出现字符不匹配的位置，

i位置固定不动，考虑j，此时已匹配相同的部分是"ababab"，它的pmt值为4，即pmt[j-1]=next[j]=4;接着就是j = next[j],让A[i]和B[j]继续进行比较；

 

 

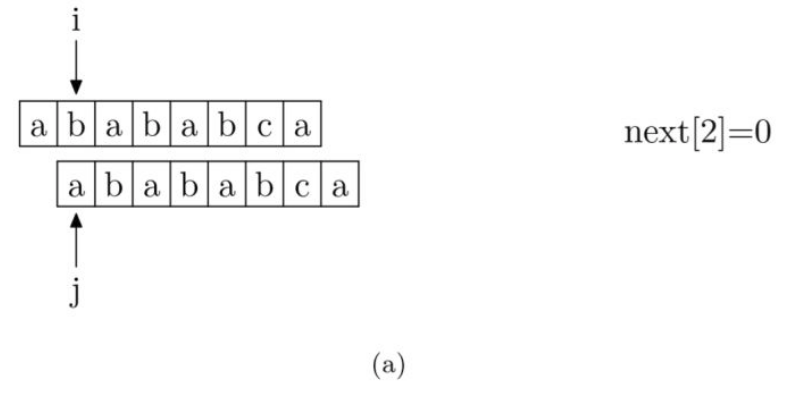
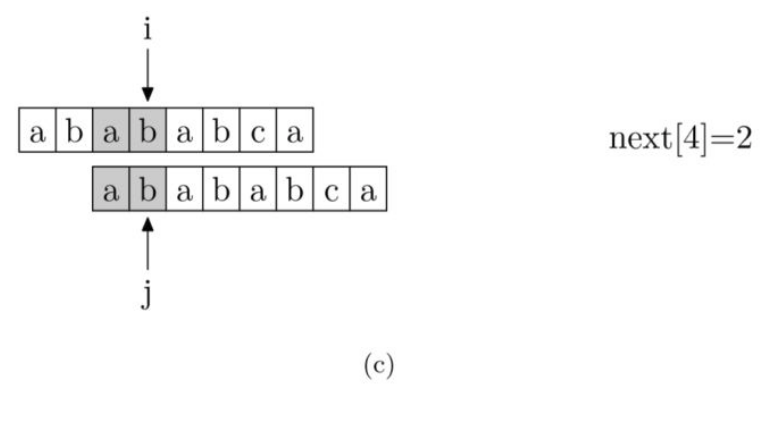
 关于getNext方法有如下图解，图（a)起始位置注意错开一位，因为pmt不含自身。由next[i] = pmt[i-1]（i >= 1）,对下图a有next[2] = pmt[1] =0;

 

 

 

public class KMP {


    public int KMP(String haystack,String needle) {
        if(haystack == null){
            throw new IllegalArgumentException("haystack is empty!");
        }
        if(needle == null || needle.trim().length() ==0){
            return 0;
        }
        char[] A = haystack.toCharArray();
        char[] B = needle.toCharArray();
        int[] next = getNext(B);

        int i = 0;
        int j = 0;

        while (i < A.length && j < B.length) {
            //j = -1,next[0]=-1, j = 0; A[i] != B[0],说明上一次B在初始位置与A[i]进行比对不成功，i向右移位一个位置，j=next[0]=-1,则巧妙地利用j++让j回到起始位置。
            if (j == -1 || A[i] == (B[j])) {
                i++;
                j++;
            } else {
                //位于A中i之前和B中j之前成功匹配的区段为PMT区段，A的PMT后缀与B的PMT前缀对齐，接下来继续比较A[i]和B[j]；
                j = next[j];
            }
        }

        if (j == B.length) {
            return i - j;
        } else {
            return -1;
        }
    }

    /**
     * 求next数组这里，targetStr既是被考察字符串也是目标字符串；自己和自己进行匹配；
     * <p>
     * next[i] = pmt[i-1],
     * 通俗点说，next[i]指的是targetStr[0,i-1]范围字符组成字符串的pmt值；
     * @param targetStr
     * @return
     */
    int[] getNext(char[] targetStr) {
        int[] next = new int[targetStr.length];
        next[0] = -1;
        int i = 0, j = -1;//注意！求pmt时不包含自身，所以要错开一位

        while (i < targetStr.length - 1) {
            if (j == -1 || targetStr[i] == (targetStr[j])) {
                //i向后移动一位
                ++i;
                //j==-1,回到初始位置；targetStr[i] == (targetStr[j]),j则向后移动一位
                ++j;
                //index在[1...targetStr.length -1]范围内next[index]满足，next[i + 1] = pmt[i] = j;
                //next[i] = pmt[i-1] = j;
                next[i] = j;
            } else {
                j = next[j];
            }
        }
        return next;
    }

 

理解KMP算法高效的关键点 ！

j = next[j];

上面代码中有这么一行代码，作用就是让被探查的已匹配成功区段的PMT后缀与目标字符串的PMT前缀对齐。如果PMT > 0 ,我们就可以跳过一些元素，那么为啥可以跳过呢？

 

 

参考上图，这里采用反证法证明。

被查询字符串是上面的”MISSISSIPPI“，目标字符串是"ISSIP"，

黄色和粉色的方块分别表示朴素方式和KMP方式；对于朴素方式， P(绿)与S(蓝)不匹配，绿色指针将回到I(黄)位置与纵向对应位置的蓝色元素继续进行比对；对于KMP方式，绿色指针跳到S(粉)位置，蓝色元素的指针位置不对变，继续比对；

粉色相对黄色不在对位于PMT元素(红色填充的元素)之间的S S I 三个位置进行比对， 这三个元素为啥可以跳过呢？

第一个蓝色的S,姑且称之为S1，假设蓝色方阵S1位置开始能够与ISSIP进行完整匹配，那么S1到第二个红色I这一段必然与ISSIP的某一前缀相同，但是这与PMT值是I冲突，所以假设不成立！对于第二个S同理！

结论：对于被查询字符串，已匹配成功区段的PMT的前缀后缀之间的元素可以被跳过检测。

红色的I为啥能跳过呢？

这完全就是利用PMT特性，PMT前缀=PMT后缀，完全是平移对齐而已，也不必检测了。

 

 

 

 

 

 

 

 

 

 

 

 

 参考：https://www.zhihu.com/question/21923021/answer/281346746