【论文系列】DDIM ---DDPM上的优化
What
DDIM是啥?
DDIM(Denoising Diffusion Implicit Models) 是一种扩散模型的变体,旨在加速图像生成过程并保持生成质量。它是在DDPM(Denoising Diffusion Probabilistic Models)的基础上发展出来的,提供了一种更高效的去噪采样过程,减少了采样所需的步骤数量。
Why
DDIM提出了能干啥?
DDPM介绍了经典扩散模型DDPM的原理和实现,对于扩散模型来说,一个最大的缺点是需要设置较长的扩散步数才能得到好的效果,这导致了生成样本的速度较慢,比如扩散步数为1000的话,那么生成一个样本就要模型推理1000次。
这就很慢很慢很慢。。。。。
但DDIM可以大大缩短这个过程
What
那它是怎么做到的啊?
1、DDIM不再限制过程必须是一个马尔可夫链,
2、DDIM的另外是一个特点是从一个随机噪音生成样本的过程是一个确定的过程(中间没有加入随机噪音)。
下面我们来着重讲讲这两句话。。
首先来回顾一下DDPM的加噪过程:
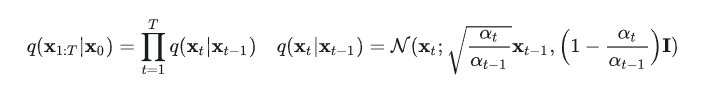
扩散过程一个很重要的特征就是可以被直接表示成用\(x_0\)对任意的\(x_t\)进行采样:
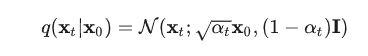
DDPM的反向去噪过程也可以定义为一个马尔可夫链:
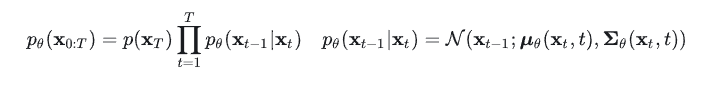

然后我们就可以得到上面的这个过程图。
这时我们猛然发现(细说猛然发现):
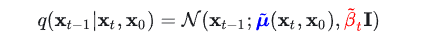
这个后验概率是一个可获取的高斯分布,它的方差是一个定值,它的均值却需要依赖于\(x_0\)和\(x_t\)
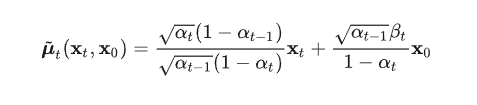
这说明了什么?
这说明了我们只要知道了原始图像和完全加噪后的图像,就可以知道去噪的噪声是什么样子!!!
根据原始论文,我们得到了如下的Objective,也就是DDPM的优化目标:
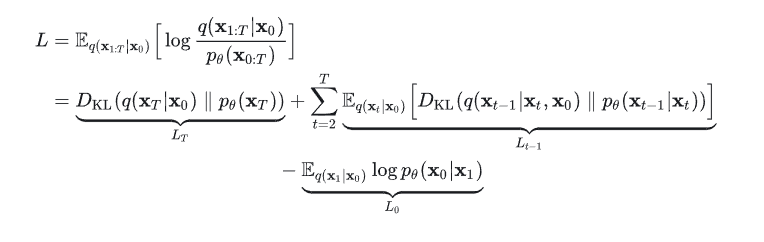
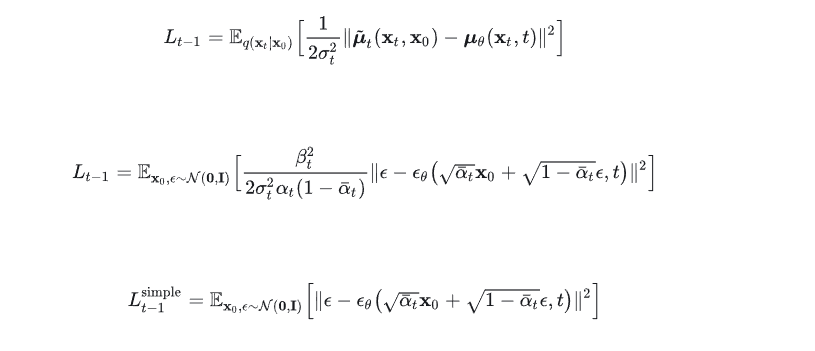
往下推推推。。。。
我们发现这个损失函数,就仅仅依赖于边缘分布\(q(x_t|x_0)\),它不直接作用在联合分布\(q(x_{1:T}|x_0)\),这说明了什么?
这说明了\(DDPM\)这个隐变量模型可以有很多推理分布来选择,只要推理分布满足边缘分布条件(扩散过程的特性)即可,而且这些推理过程并不一定要是马尔卡夫链。
DDIM的论文这么定义的:
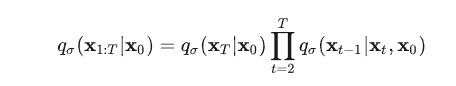
其中上式子还要满足如下这些:
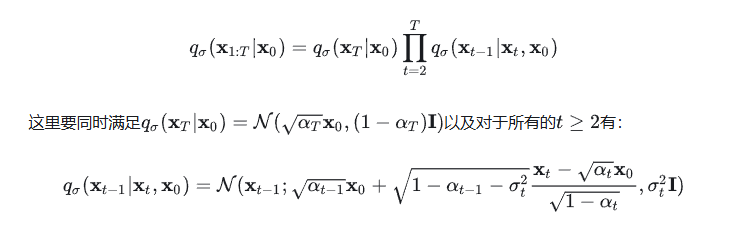


 浙公网安备 33010602011771号
浙公网安备 33010602011771号