个人项目：论文查重

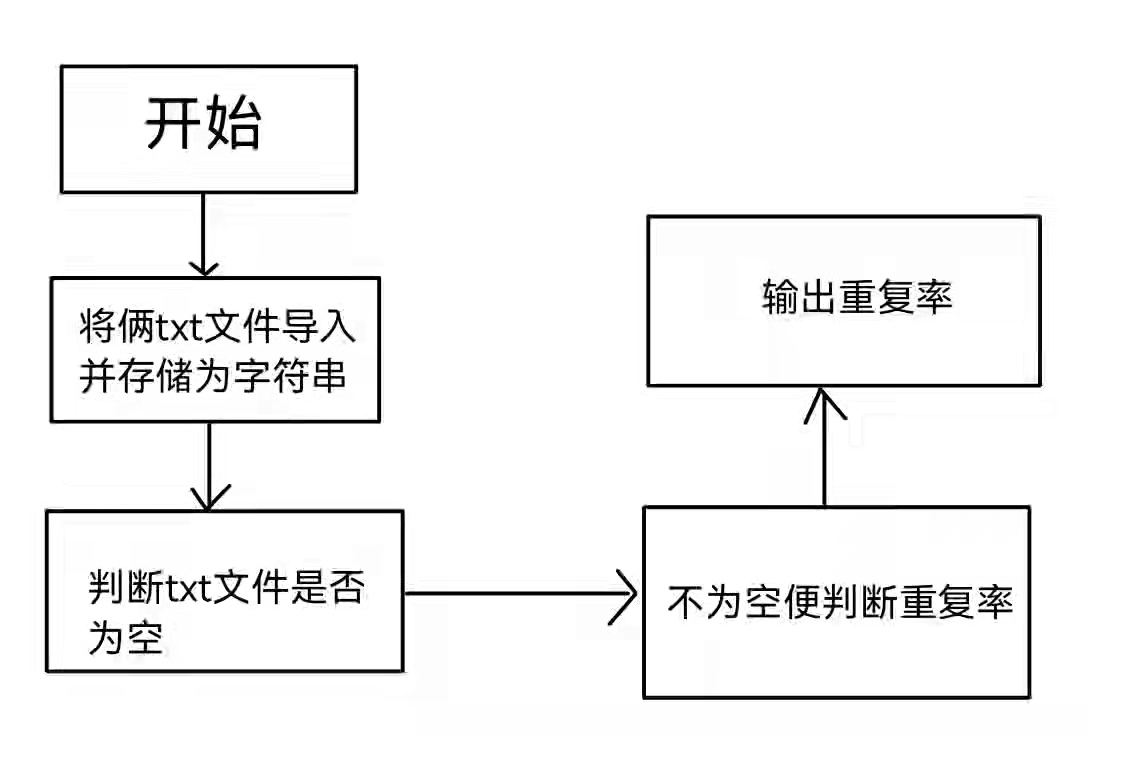
这个作业属于哪个课程	软件工程
这个作业要求在哪里	作业要求
这个作业的目标	[学会上传文件至GitHub，学会编写查重编程]

1.GitHub地址

2.PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	40
Estimate	估计这个任务需要多少时间	25	30
Development	开发	1080	1140
Analysis	求分析 (包括学习新技术)	240	220
Design Spec	生成设计文档	20	30
Design Review	设计复审	30	40
Coding Standard	代码规范 (为目前的开发制定合适的规范)	10	10
Design	具体设计	60	90
Coding	具体编码	450	540
Code Review	代码复审	20	25
Test	测试（自我测试，修改代码，提交修改）	15	30
Reporting	报告	50	45
Test Repor	测试报告	20	20
Size Measurement	计算工作量	15	15
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	15	25
Sum up	合计	2080	2300

3.计算模块接口的设计与实现过程:

文本相似度计算之余弦定理
相似度计算方法：余弦相似度

通过查阅资料，我了解到目前的主流查重方法有两种，分别是余弦相似和海明距离，此次作业，我用的是余弦相似来做的。

余弦相似定理就是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值，绘制到向量空间中。用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，反之越接近0就表示两个向量相似度越低。

我们来看一个例子：

句子A：我喜欢看电视，不喜欢看电影。

句子B：我不喜欢看电视，也不喜欢看电影。

第一步，分词。

　　句子A：我/喜欢/看/电视，不/喜欢/看/电影。

　　句子B：我/不/喜欢/看/电视，也/不/喜欢/看/电影。

第二步，列出所有的词。

　　我，喜欢，看，电视，电影，不，也。

第三步，计算词频。

　　句子A：我 1，喜欢 2，看 2，电视 1，电影 1，不 1，也 0。

　　句子B：我 1，喜欢 2，看 2，电视 1，电影 1，不 2，也 1。

第四步，写出词频向量。

　　句子A：[1, 2, 2, 1, 1, 1, 0]

　　句子B：[1, 2, 2, 1, 1, 2, 1]

到了这里问题就变成了如何计算这两个向量的相似程度。

我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

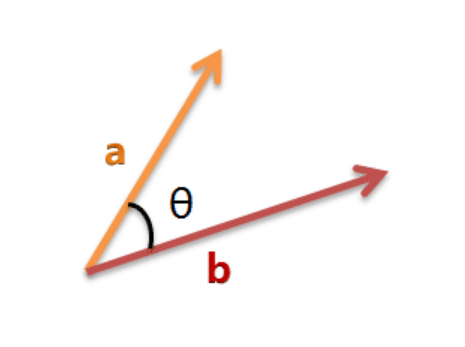
假定a向量是[x1, y1]，b向量是[x2, y2]，那么可以将余弦定理改写成下面的形式：

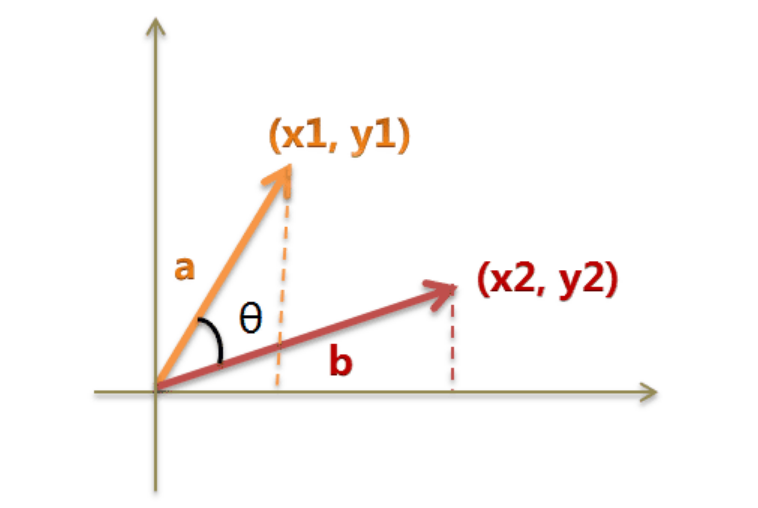
那么余弦公式就为：

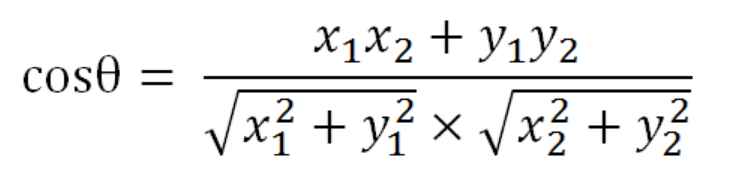
假定A和B是两个n维向量，A是 [A1, A2, ..., An] ，B是 [B1, B2, ..., Bn] ，则A与B的夹角θ的余弦等于：

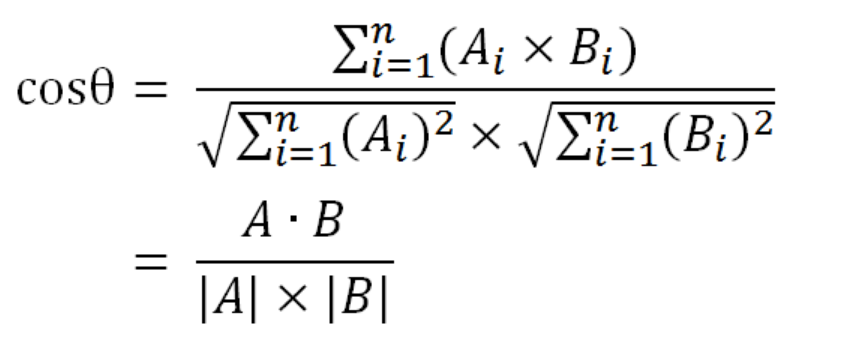
因此上面对比的两个句子，就可以用公式来判断余弦相似

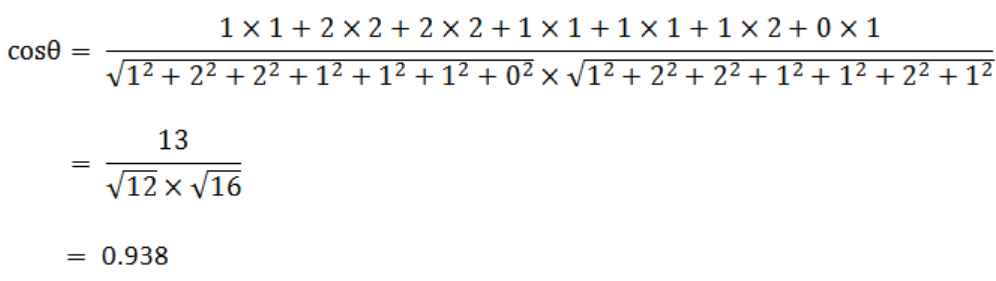
余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。所以，上面的句子A和句子B是很相似的

4.计算模块接口部分的性能

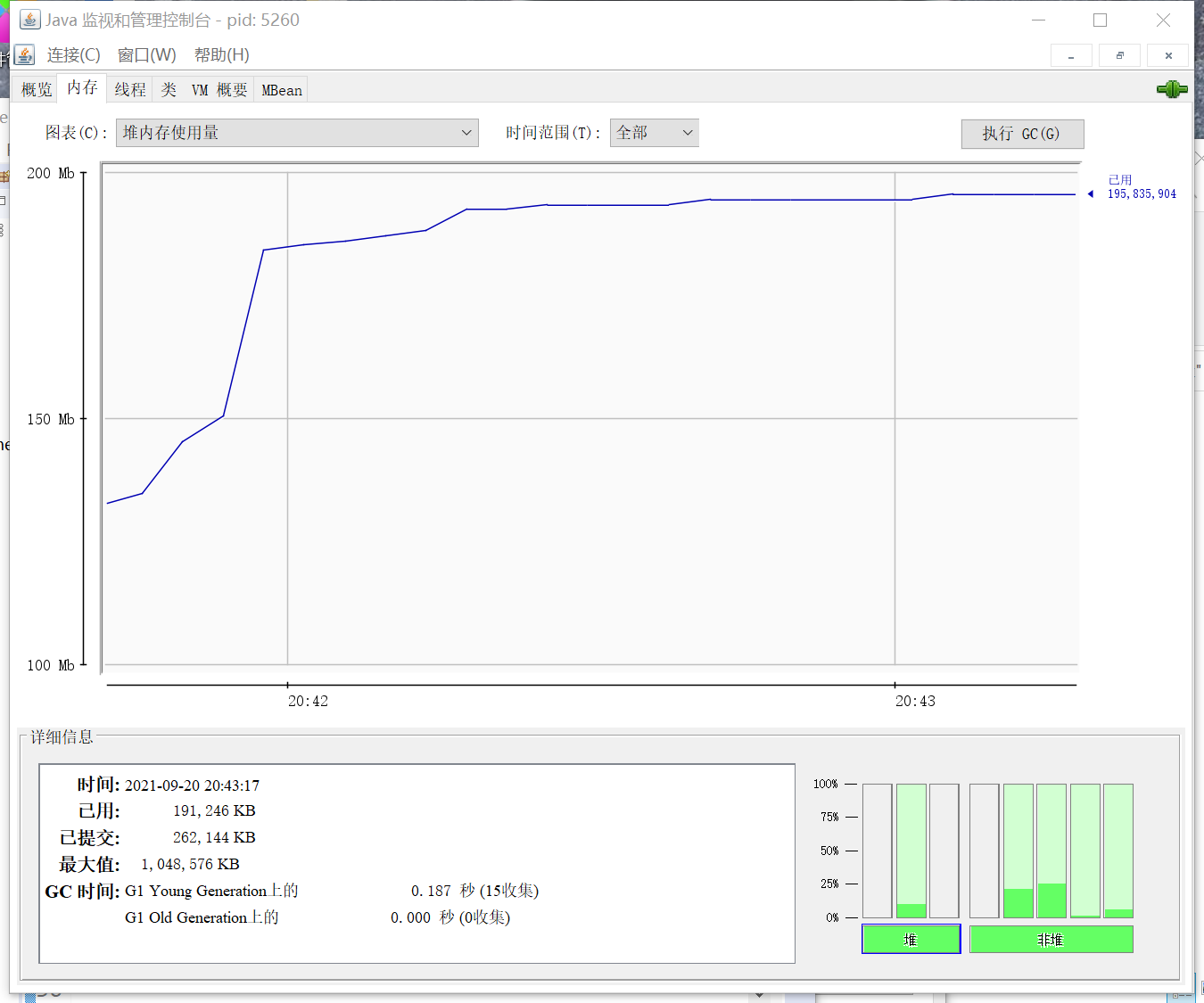
5.计算模块部分单元测试展示

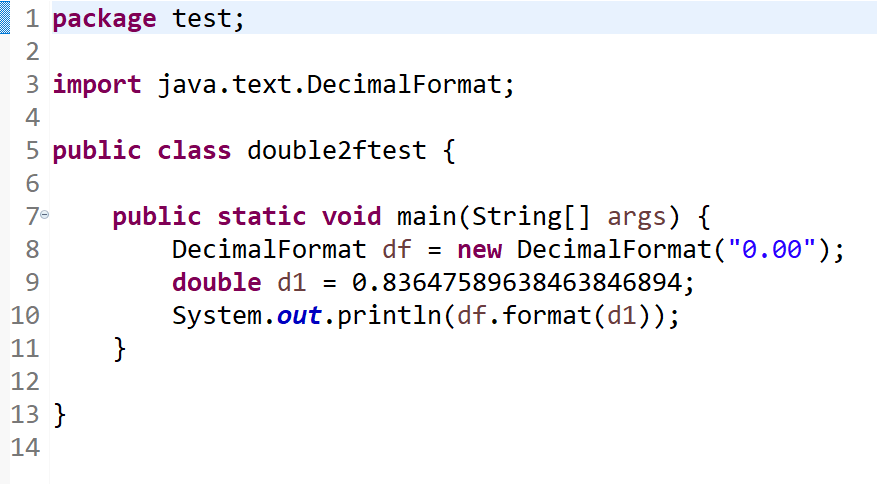
6.计算模块部分异常处理说明

总结：这次个人项目我做的比较吃力，深深体会到了我的不足，该程序还仍然有点小问题，计算模块部分异常有些许问题（会输出重复率很大，但明明应该重复率为0），我会继续跟进该作业，有新的想法和改进方法都会再重新上传，非常感谢。