动态规划(1)
最长递增子序列
动态规划的核⼼设计思想是数学归纳法。
题目

分析
我们的定义是这样的:dp[i] 表⽰以 nums[i] 这个数结尾的最⻓递增⼦序列的⻓度。
题解
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// dp 数组全都初始化为 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
总结⼀下动态规划的设计流程:
1、⾸先明确 dp 数组所存数据的含义。这步很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
2、然后根据 dp 数组的定义,运⽤数学归纳法的思想,假设 dp[0...i-1] 都已知,想办法求出 dp[i] ,⼀旦这⼀步完成,整个题⽬基本就解决了。
但如果⽆法完成这⼀步,很可能就是 dp 数组的定义不够恰当,需要重新定
义 dp 数组的含义;或者可能是 dp 数组存储的信息还不够,不⾜以推出下⼀
步的答案,需要把 dp 数组扩⼤成⼆维数组甚⾄三维数组。
3、最后想⼀想问题的 base case 是什么,以此来初始化 dp 数组,以保证算法正
确运⾏。
0-1背包问题
题目
这个题⽬中的物品不可以分割,要么装进包⾥,要么不装,不能说切成两块装⼀半。这就是 0-1 背包这个名词的来历。
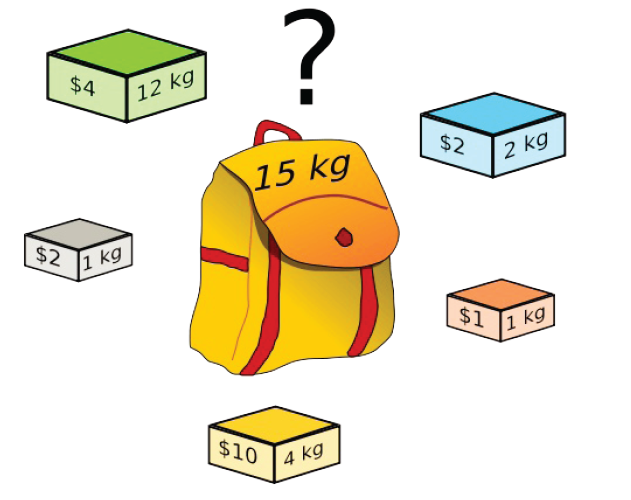
解决这个问题没有什么排序之类巧妙的⽅法,只能穷举所有可能。
分析
1、第⼀步要明确两点,「状态」和「选择」。
1)先说状态,如何才能描述⼀个问题局⾯?只要给⼏个物品和⼀个背包的容量限制,就形成了⼀个背包问题呀。所以状态有两个,就是「背包的容量」和「可选择的物品」。
2)再说选择,也很容易想到啊,对于每件物品,你能选择什么?选择就是「装进背包」或者「不装进背包」嘛。
明⽩了状态和选择,动态规划问题基本上就解决了,只要往这个框架套就完事⼉了:
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
2、第⼆步要明确 dp 数组的定义。
⾸先看看刚才找到的「状态」,有两个,也就是说我们需要⼀个⼆维 dp数组。
dp[i][w] 的定义如下:对于前 i 个物品,当前背包的容量为 w ,这种情况下可以装的最⼤价值是 dp[i][w] 。根据这个定义,我们想求的最终答案就是 dp[N][W] 。
base case 就是 dp[0][..] = dp[..][0] = 0 ,因为没有物品或者背包没有空间的时候,能装的最⼤价值就是 0。
int dp[ N + 1][W + 1]
dp[0][..] =0
dp[..][0] =0
for i in[ 1..N]:
for w in[ 1..W]:
dp[i][w] = max(
把物品 i 装进背包,
不把物品 i 装进背包
)
return dp[N][W]
3、第三步,根据「选择」,思考状态转移的逻辑。
简单说就是,上⾯伪码中「把物品 i 装进背包」和「不把物品 i 装进背包」怎么⽤代码体现出来呢?这就要结合对 dp 数组的定义和我们的算法逻辑来分析。
1) 如果你没有把这第 i 个物品装⼊背包,那么很显然,最⼤价值 dp[i][w]应该等于 dp[i-1][w] ,继承之前的结果。
2) 如果你把这第 i 个物品装⼊了背包,那么 dp[i][w] 应该等于 dp[i-1][w- wt[i-1]] + val[i-1] 。
for i in [1..N]:
for w in [1..W]:
dp[i][w] = max(
dp[i-1][w],
dp[i-1][w - wt[i-1]] + val[i-1]
)
return dp[N][W]
4、最后⼀步,把伪码翻译成代码,处理⼀些边界情况。
题解
int knapsack(int W, int N, vector<int>& wt, vector<int>& val) {
// base case 已初始化
vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
if (w - wt[i-1] < 0) {
// 边界情况,这种情况下只能选择不装⼊背包
dp[i][w] = dp[i - 1][w];
} else {
// 装⼊或者不装⼊背包,择优
dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1],
dp[i - 1][w]);
}
}
}
return dp[N][W];
}
0-1背包之——相等子集分隔
题目
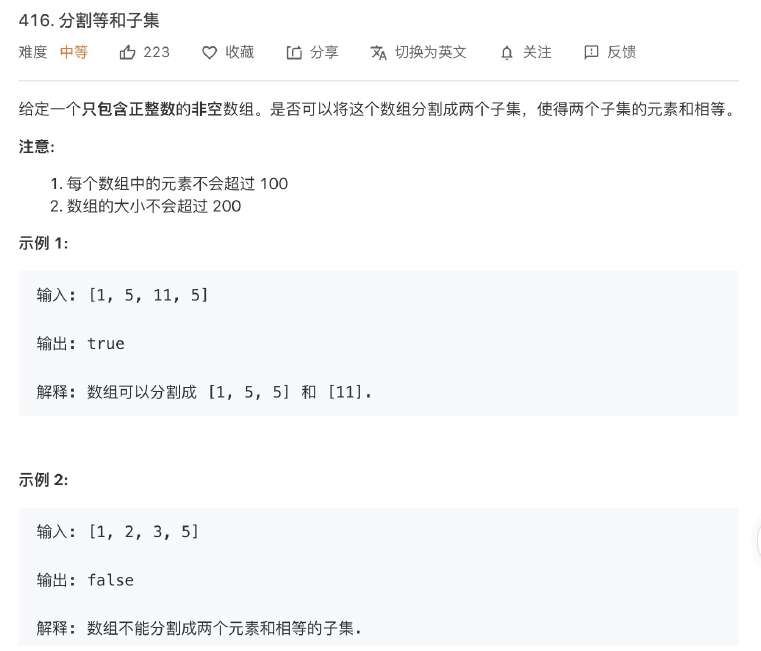
分析
那么对于这个问题,我们可以先对集合求和,得出 sum ,把问题转化为背包问题:
给⼀个可装载重量为 sum / 2 的背包和 N 个物品,每个物品的重量为nums[i] 。现在让你装物品,是否存在⼀种装法,能够恰好将背包装满?
1、第⼀步要明确两点,「状态」和「选择」。
状态就是「背包的容量」和「可选择的物品」,选择就是「装进背包」或者「不装进背包」。
2、第⼆步要明确 dp 数组的定义。
按照背包问题的套路,可以给出如下定义:
dp[i][j] = x 表⽰,对于前 i 个物品,当前背包的容量为 j 时,若 x为 true ,则说明可以恰好将背包装满,若 x 为 false ,则说明不能恰好将背包装满。
我们想求的最终答案就是 dp[N][sum/2] ,base case 就是dp[..][0] = true 和 dp[0][..] = false ,因为背包没有空间的时候,就相当于装满了,⽽当没有物品可选择的时候,肯定没办法装满背包。
3、第三步,根据「选择」,思考状态转移的逻辑。
回想刚才的 dp 数组含义,可以根据「选择」对 dp[i][j] 得到以下状态转移:
如果不把 nums[i] 算⼊⼦集,或者说你不把这第 i 个物品装⼊背包,那么是否能够恰好装满背包,取决于上⼀个状态 dp[i-1][j] ,继承之前的结果。
如果把nums[i]算⼊⼦集,或者说你把这第 i 个物品装⼊了背包,那么是否能够恰好装满背包,取决于状态 dp[i - 1][j-nums[i-1]] 。
注意:由于 i 是从 1 开始的,⽽数组索引是从 0 开始的,所以第 i 个物品的重量应该是 nums[i-1] ,这⼀点不要搞混。
4、最后⼀步,把伪码翻译成代码,处理⼀些边界情况。
题解
bool canPartition(vector<int>& nums) {
int sum = 0;
for (int num : nums) sum += num;
// 和为奇数时,不可能划分成两个和相等的集合
if (sum % 2 != 0) return false;
int n = nums.size();
sum = sum / 2;
vector<vector<bool>>
dp(n + 1, vector<bool>(sum + 1, false));
// base case
for (int i = 0; i <= n; i++) {
dp[i][0] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= sum; j++) {
if (j - nums[i - 1] < 0) {
// 背包容量不⾜,不能装⼊第 i 个物品
dp[i][j] = dp[i - 1][j];
} else {
// 装⼊或不装⼊背包
dp[i][j] = dp[i - 1][j] | dp[i - 1][j-nums[i-1]];
}
}
}
return dp[n][sum];
}
完全背包-零钱兑换
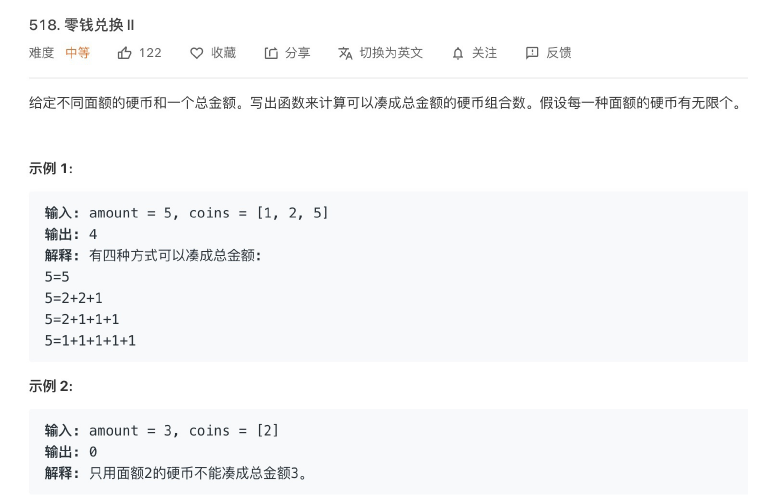
这个问题和我们前⾯讲过的两个背包问题,有⼀个最⼤的区别就是,每个物品的数量是⽆限的,这也就是传说中的「完全背包问题」,没啥⾼⼤上的,⽆⾮就是状态转移⽅程有⼀点变化⽽已。
分析
1、第⼀步要明确两点,「状态」和「选择」。(与0-1背包相同)
2、第⼆步要明确 dp 数组的定义。(与0-1背包相同)
⾸先看看刚才找到的「状态」,有两个,也就是说我们需要⼀个⼆维 dp数组。
dp[i][j] 的定义如下:
若只使⽤前 i 个物品,当背包容量为 j 时,有 dp[i][j] 种⽅法可以装满背包。
即,若只使⽤ coins 中的前 i 个硬币的⾯值,若想凑出⾦额 j ,有 dp[i][j] 种凑法。base case 为 dp[0][..] = 0, dp[..][0] = 1 。因为如果不使⽤任何硬币⾯值,就⽆法凑出任何⾦额;如果凑出的⽬标⾦额为 0,那么“⽆为⽽治”就是唯⼀的⼀种凑法。
3、第三步,根据「选择」,思考状态转移的逻辑。((与0-1背包不同点)
注意,我们这个问题的特殊点在于物品的数量是⽆限的,所以这⾥和之前写的背包问题⽂章有所不同。
如果你不把这第 i 个物品装⼊背包,也就是说你不使⽤ coins[i] 这个⾯值的硬币,那么凑出⾯额 j 的⽅法数 dp[i][j] 应该等于 dp[i-1][j] ,继承之前的结果。
如果你把这第 i 个物品装⼊了背包,也就是说你使⽤ coins[i] 这个⾯值的硬币,那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]] 。
注意:由于 i 是从 1 开始的,所以 coins 的索引是 i-1 时表⽰第 i 个硬币的⾯值。
综上就是两种选择,⽽我们想求的 dp[i][j] 是「共有多少种凑法」,所以dp[i][j] 的值应该是以上两种选择的结果之和。
4、最后⼀步,把伪码翻译成代码,处理⼀些边界情况。(与0-1背包相同)
题解
int change(int amount, int[] coins) {
int n = coins.length;
int[][] dp = amount int[n + 1][amount + 1];
// base case
for (int i = 0; i <= n; i++)
dp[i][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= amount; j++)
if (j - coins[i-1] >= 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
} else {
dp[i][j] = dp[i - 1][j];
}
}
return dp[n][amount];
}
</vector




