信息学奥赛复赛复习09-CSP-J2020-03表达式求值前置知识点-中缀表达式求值、摸运算、模运算性质、栈

PDF文档公众号回复关键字:20241002

1 P1981 [NOIP2013普及组] 表达式求值

[题目描述]

给定一个只包含加法和乘法的算术表达式，请你编程计算表达式的值

[输入格式]

一行，为需要你计算的表达式，表达式中只包含数字、加法运算符 “+” 和乘法运算符 “×”，且没有括号，所有参与运算的数字均为 0 到 2^31之间的整数。

输入数据保证这一行只有 0∼9、+、× 这 12种字符

[输出格式]

一个整数，表示这个表达式的值。

注意：当答案长度多于 4 位时，请只输出最后 4 位，前导 0 不输出

[输入输出样例]

输入 #1

1+1*3+4

输出 #1

8

输入 #2

1+1234567890*1

输出 #2

7891

输入 #3

1+1000000003*1

输出 #2

4

说明/提示

对于 30% 的数据，0≤ 表达式中加法运算符和乘法运算符的总数 ≤100。

对于 80% 的数据，0≤ 表达式中加法运算符和乘法运算符的总数 ≤1000。

对于 100% 的数据，0≤ 表达式中加法运算符和乘法运算符的总数 ≤100000。

2 相关知识点

1) 模运算

模运算，就是取余数，在计算机语言中用%来表示。举个简单的例子，3 % 5 = 3。结果的取值范围在 0 与模之间

例如

c=x/y

c=3 mod 5 =3 c的取值范围 [0,y-1]

结果也可以用负数表示，即 c=-2

2) 模运算性质

(a + b) % p = (a % p + b % p) % p

(a - b) % p = (a % p - b % p ) % p

(a * b) % p = (a % p * b % p) % p

a ^ b % p = ((a % p)^b) % p

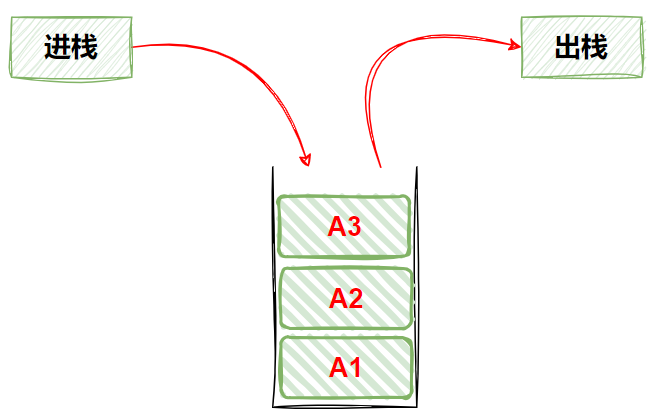
3) 栈

栈又名堆栈，是一种限定仅在表尾进行插入和删除操作的线性表，这一端称为栈顶，另一端称为栈底

栈中的数据元素遵守后进先出的原则

4) 中缀表达式

是一种常见的算术表达式表示方法，其中运算符位于操作数之间

例如

//示例1
3 + 4 * 2
//示例2
(1 + 2) * (3 - 4)

3 思路分析

由于本题只有2个操作数，+和*，且*的优先级大于+
因此可以提前先把*计算出来，剩余都是+运算符，再统一计算加
例如如下表达式，具体步骤如下
1+1*3+4

每次输入一个操作符和一个操作数
遇到*号，从栈中取出栈顶操作数和本次读取的操作数相乘
相乘的结果存入栈中

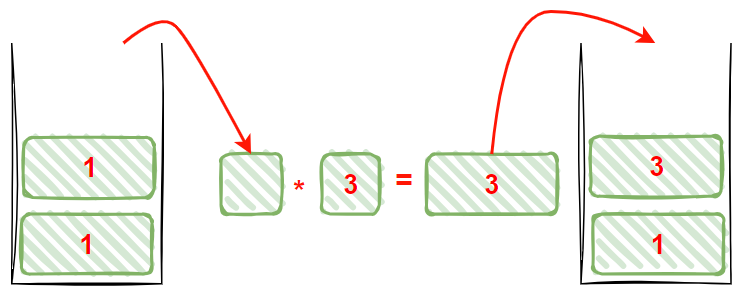
2读入下一个操作符+和操作数4
直接把4放入栈中

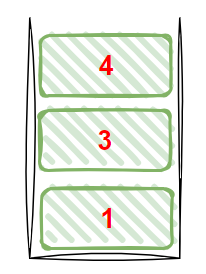
3 栈中3个操作数只剩下1种操作符+
遍历栈对这3个操作数相加，即为表达式的值

示例程序

#include<bits/stdc++.h>
using namespace std;
/*
栈 
1 存储 *前的操作数和相乘后的结果 
2 存储 + 号前后的操作数 
*/ 
stack<int> st; 
int f,t,ans;//f第1个操作数 t第2个操作数 ans运算结果 
char s;//操作符 
const int m=10000;//只输出最后4位，结果对m取模 
int main(){
	cin>>f;//输入第1个操作数 
	st.push(f%10000);//根据模运算乘法和加法性质，可以先取模 
	while(cin>>s>>t){//输入操作符号和第2个操作数，直到结束 
		if(s=='*'){//乘法提前计算结果，再存入栈，保证栈中只保留加法运算 
			f=st.top();//从栈中取出第1个操作数 
			st.pop();//弹出上面取出的操作数 
			/*
			  把结算结果存入栈，后续把结果相加 
			  根据模运算加法性质，可以先取模 
			*/
			st.push(f*t%m);
		}else{//加法操作符 直接存入栈，后续取出相加 
			st.push(t);
		}
	}
	//遍历栈，栈中保留的都是加法操作数，可以直接相加 
	while(st.size()!=0){//遍历栈，直到没有任何元素 
		ans=(ans+st.top())%m;//把栈中每个数累加到ans 
		st.pop();//累加后 从栈中弹出 
	}
	cout<<ans;//输出运算结果 
	return 0;
}