信息学奥赛初赛天天练-72-NOIP2016普及组-基础题3-无向图、简单无向图、自环、平行边、顶点的度、握手定理、递归

NOIP 2016 普及组基础题3

5 以下不是存储设备的是( )
A 光盘
B 磁盘
C 固态硬盘
D 鼠标

6 如果开始时计算机处于小写输入状态，现在有一只小老鼠反复按照 CapsLock、字母键 A、字母键 S、字母键 D、字母键 F 的顺序循环按键，即 CapsLock、A、S、D、F、CapsLock、A、S、D、F、……，屏幕上输出的第 81 个字符是字母 ( )
A A
B S
C D
D a

13 有以下程序

#include <iostream>
using namespace std;
int main()
{
    int k = 4, n = 0;
    while (n < k)
    {
        n++;
        if (n % 3 != 0)
            continue;
        k--;
    }
    cout << k << "," << n << endl;
    return 0;
}

程序运行后输出的结果是

A 2,2
B 2,3
C 3,2
D 3,3

14 给定含有 n个不同的数的数组 L=<x1,x2,...,xn>。如果 L中存在 xi(1<i<n) 使得 x1<x2<⋯<xi−1< xi >xi+1>⋯>xn，则称 L 是单峰的，并称 xi是 L的“峰顶”。现在已知 L 是单峰的,请把 a-c 三行代码补全到算法中使得算法正确找到 L的峰顶
a Search(k+1, n)
b Search(1, k-1)
c return L[k]

Search(1, n)
1. k←⌊n/2⌋
2. if L[k] > L[k-1] and L[k] > L[k+1]
3. then __________
4. else if L[k] > L[k-1] and L[k] < L[k+1]
5. then __________
6. else __________

正确的填空顺序是( )

A c,a,b
B c,b,a
C a,b,c
D b,a,c

15 设简单无向图 G有 16条边且每个顶点的度数都是 2，则图 G 有( )个顶点

A 10
B 12
C 8
D 16

2 相关知识点

1) 无向图

图的边没有方向

自环

即一条连接一个顶点和其自身的边

平行边

连接同一对顶点的两条边

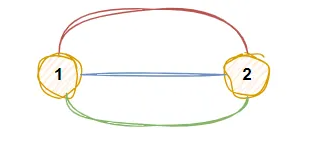
简单无向图

一个简单无向图是一个无向图，其中不存在重复边和自环（即一个顶点连接到其自身）

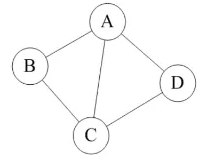
2) 顶点的度

无向图中与顶点相连的边的数目，称为顶点的度

下图中A点的度为3

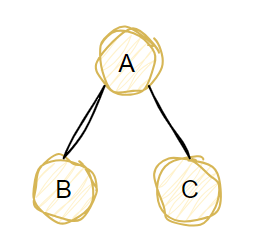
3) 握手定理

无向图中结点度数的总和等于边数的两倍

下图边数为2，A点的度为2，B点的度为1，C点的度为1，ABC3点的度数之和2+1+1=4

为边数的两倍

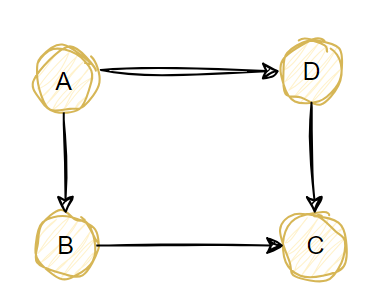
有向图中结点入度的和等于出度的和等于边数

如下有向图，边数为4

出度为 A的出度为2，B的出度为1，C的出度为0，D的出度为1，所以出度和为2+1+0+1=4

入度为A的入度为0， B的入度为1，C的入度为2，D的入度为1，所以入度和为0+1+2+1=4

所以下图边数、入度和、出度和都相等

5) 递归

递归是一种解决问题的方法，它通过将问题分解为更小的子问题来解决。

一个递归函数会在其定义中直接或间接地调用自身

递归通常包括两个部分：基本情况（Base case）和递归步骤（Recursive step）。

基本情况是指当问题规模变得足够小时，可以直接得到解决方案的情况

3 思路分析

5 以下不是存储设备的是( D )
A 光盘
B 磁盘
C 固态硬盘
D 鼠标

分析

A 光盘是一种光学存储介质，用于存储数据和信息，是存储设备。
B 磁盘是一种磁性存储介质，通常用于计算机系统中存储数据和信息，是存储设备。
C 固态硬盘是一种基于闪存技术的存储设备，用于存储数据和信息，是存储设备。
D. 鼠标：鼠标是一种输入设备，用于与计算机系统进行交互，不是存储设备。
因此选D

6 如果开始时计算机处于小写输入状态，现在有一只小老鼠反复按照 CapsLock、字母键 A、字母键 S、字母键 D、字母键 F 的顺序循环按键，即 CapsLock、A、S、D、F、CapsLock、A、S、D、F、……，屏幕上输出的第 81 个字符是字母 ( A )
A A
B S
C D
D a

分析

根据题意可知，屏幕输出字符
ASDFasdf...
按4个1组，1组大写，2组小写，3组大写，4组小写...
每奇数组为大写，每偶数组为小写
⌈81/4⌉=21 ,为奇数，所以为大写字母，是大写字母的第1个，所以为A

13 有以下程序

#include <iostream>
using namespace std;
int main()
{
    int k = 4, n = 0;
    while (n < k)
    {
        n++;
        if (n % 3 != 0)
            continue;
        k--;
    }
    cout << k << "," << n << endl;
    return 0;
}

程序运行后输出的结果是( D )

A 2,2
B 2,3
C 3,2
D 3,3

分析

初始 n=0 k=4
0<4 条件成立  n++后n=1 ，1%3!=0 条件成立 k不变 k=4
1<4 条件成立  n++后n=2 ，2%3!=0 条件成立 k不变 k=4
2<4 条件成立  n++后n=3 ，3%3!=0 条件不成立 k-- k=3
3<3 条件不成立，退出while循环，输出k=3 n=3
所以选D

Search(1, n)
1. k←⌊n/2⌋
2. if L[k] > L[k-1] and L[k] > L[k+1]
3. then __________
4. else if L[k] > L[k-1] and L[k] < L[k+1]
5. then __________
6. else __________

正确的填空顺序是( A )

A c,a,b
B c,b,a
C a,b,c
D b,a,c

分析

2. if L[k] > L[k-1] and L[k] > L[k+1]
比左边大且比右边大，说明此时最高，返回return L[k]
4. else if L[k] > L[k-1] and L[k] < L[k+1]
比左边大，比右边小，说明还未到最高，继续向右边找 Search(k+1, n)
否则 向左边找 Search(1, k-1)

15 设简单无向图 G有 16条边且每个顶点的度数都是 2，则图 G 有( D )个顶点

A 10
B 12
C 8
D 16

分析

根据握手定理，一个无向图的所有顶点的度数之和等于其边数的两倍
有16条边，因此，度数和为16*2=32
又每个顶点的度数都是2，所以总共有32/2=16个顶点

posted @ 2024-08-22 19:08 new-code 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

new-code

new-code

信息学奥赛初赛天天练-72-NOIP2016普及组-基础题3-无向图、简单无向图、自环、平行边、顶点的度、握手定理、递归

公告