信息学奥赛初赛天天练-69-NOIP2017普及组-完善程序2-切割绳子、二分答案、二分边界、二分边界、二分时间复杂度

1 完善程序 (单选题 ，每小题3分，共30分)

切割绳子

有 n 条绳子，每条绳子的长度已知且均为正整数。绳子可以以任意正整数长度切割，但不可以连接。现在要从这些绳子中切割出 m条长度相同的绳段，求绳段的最大长度是多少。（第一、二空 2.5 分，其余 3分）

输入：第一行是一个不超过 100的正整数 n，第二行是 n个不超过 10^6的正整数，表示每条绳子的长度，第三行是一个不超过 10^8的正整数 m。

输出：绳段的最大长度，若无法切割，输出 Failed

01 #include<iostream>
02 using namespace std;
03 int n, m, i, lbound, ubound, mid, count;
04 int len[100]; // 绳子长度
05 int main()
06 {
07     cin >> n;
08     count = 0;
09     for (i = 0; i < n; i++)
10     {
11         cin >> len[i];
12         ①;
13     }
14     cin >> m;
15     if (②)
16     {
17         cout << "Failed" << endl;
18         return 0;
19     }
20     lbound = 1;
21     ubound = 1000000;
22     while (③)
23     {
24         mid = ④;
25         count = 0;
26         for (i = 0; i < n; i++)
27             ⑤;
28         if (count < m)
29             ubound = mid - 1;
30         else
31             lbound = mid;
32     }
33     cout << lbound << endl;
34     return 0;
35 }

1 ①处应填( )

2 ②处应填( )

3 ③处应填( )

4 ④处应填( )

5 ⑤处应填( )

2 相关知识点

二分答案

二分答案顾名思义，它用二分的方法枚举答案，并且枚举时判断这个答案是否可行

直接对答案进行枚举查找，接着判断答案是否合法。如果合法，就将答案二分进一步靠近，如果不合法，就接着二分缩小判断。这样就可以大大的减少时间。

二分中有时可以得可行得答案，但不是最大的，继续向右靠近，求出最大值

 int ans = 1;
 int l = 1,r = 100000;//在1~100000之间的整数枚举 
 while(l <= r){
     int m = l + (r - l) / 2;
     if(check(m)){//满足 则进行向右缩小范围 看看有没有更大的 
         ans = m;//可能多次赋值 最后一定是可能的最大值 
         l = m + 1;
      }else{//不满足缩小边长 向左缩小范围 用更小边长继续尝试 
         r = m - 1;
	  } 
  }

二分查找中间值

/* 向右逼近，如果找到满足条件的数，会继续向右找更大的数，让循环结束
   mid=(left+right)/2 left和right都接近最大值时，可能溢出可以使用下面写法替换
   mid=left + (right-left) / 2;
   可以求满足条件的最大值
*/
    
/* 向左逼近，如果找到满足条件的数，会继续向左找更小的数，让循环结束
   mid=(left+right+1)/2 left和right都接近最大值时，可能溢出可以使用下面写法替换
   mid=left + (right-left+1) / 2;
   可以求满足条件的最小值
*/

二分找边界

//左闭右闭 while left right 最终left=right+1
while(left<=right)  left = mid + 1; right =mid-1;
//左闭右开 while left right 最终left=right
while(left<right)   left = mid + 1; right =mid;
//左开右闭 while left right 最终left=right
while(left<right)   left=mid;       right=mid-1;
//左开右开 while left right 最终left=right-1
while(left+1<right) left=mid;       right=mid;

二分查找时间复杂度

二分查找每次都缩小或扩大为原来的一半，所以也是Olog(n)

3 思路分析

每个棍子长度不超过10^6,且棍子切割必须为整数，因此通过二分的方法在1~ 10^6之间寻找答案

找到1个可能的棍子的长度后，计算n个棍子可以切分棍子的总数

如果总数<m,则切分不够，继续缩小棍子的长度，来切分更多的棍子

直到切分的长度大于等于m

例如

输入
3
4 6 12
7
范围缩小到 lbound=1，ubound=10时
此时mid=(1+10+1)/2=6,使用长度为6进行切分时，3个棍子分别切分为0+1+2=3不能满足m=7

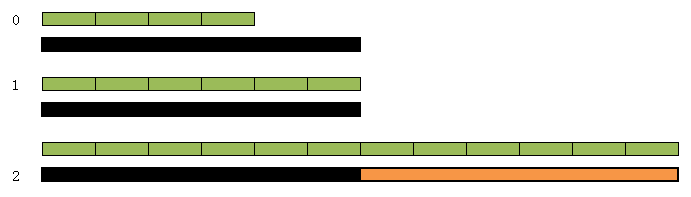
ubound=mid-1=6-1=5
此时mid=(1+5+1)/2=3,使用长度为3进行切分时，3个棍子分别切分为1+2+4=7满足m=7

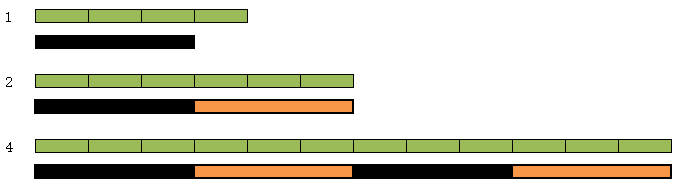
1 ①处应填( count=count+len[i] )

分析

考虑一种情况，先把棍子长度加起来，如果切成最小单位，每个棍子长度为1
这些棍子的总数比m还小，则无法切割
count=count+len[i] 可以看作把所有最小长度为1的棍子都加起来

2 ②处应填( count<m )

分析

考虑一种情况，先把棍子长度加起来，如果切成最小单位，每个棍子长度为1
这些棍子的总数比m还小，则无法切割
count 可以看作把所有最小长度为1的棍子都加起来，如果还不到m个棍子，则无法切割

3 ③处应填( lbound<ubound )

分析

根据如下二分找边界可知， lbound<ubound
//左开右闭 while left right 最终left=right
while(left<right)   left=mid;       right=mid-1;

4 ④处应填( (lbound+ubound+1)/2 )

分析

根据如下二分找中间值可知， 当特殊情况左边界值不会增加， (lbound+ubound)/2的值不变，会进入死循环
 (lbound+ubound)/2会使得左边界+1，结束循环
28         if (count < m)
29             ubound = mid - 1;
30         else
31             lbound = mid;

5 ⑤处应填( count+=len[i]/mid )

分析

二分找出一个棍子长度mid，计算所有棍子，按mid长度可以切分的棍子数量
26         for (i = 0; i < n; i++)
27             ⑤;