信息学奥赛初赛天天练-68-NOIP2017普及组-完善程序1-幂运算、快速幂、数据类型、溢出、模运算、模运算性质
PDF文档公众号回复关键字:20240818

1 完善程序 (单选题 ,每小题3分,共30分)
快速幂
请完善下面的程序,该程序使用分治法求 x^p mod m 的值。(第一空 2 分,其余 3 分)
输入:三个不超过 10000 的正整数 x,p,m
输出:x^p mod m的值
01 #include<iostream>
02 using namespace std;
03 int x, p, m, i, result;
04 int main(){
05 cin >> x >> p >> m;
06 result = ①;
07 while (②){
08 if (p % 2 == 1)
09 result = ③;
10 p /= 2;
11 x = ④;
12 }
13 cout << ⑤ << endl;
14 return 0;
15}
1 ①处应填( )
2 ②处应填( )
3 ③处应填( )
4 ④处应填( )
5 ⑤处应填( )
2 相关知识点
1) 幂
x的n次幂,是指x的n次方,也就是n个x相乘,比如2的4次幂就是2 * 2 * 2 * 2
#include<bits/stdc++.h>
using namespace std;
/*
朴素算法计算x的n次幂
n个x相乘
*/
int x,n,result=1;
int main(){
cin>>x>>n;
for(int i=0;i<n;i++){
result=result * x;
}
cout<<result;
return 0;
}
/*
输入 2 10
输出 1024
*/
2) 快速幂
快速幂用于快速计算整数的整数幂,支持取模,其算法思想是“倍增”
就是用效率更高(时间复杂度更低)的方法求幂,可以将时间复杂度优化至O(logn)
#include<iostream>
using namespace std;
int x, p,i, result;
/*
快速幂
指数除以2,底数倍增是等价的
例如 2^4=4^2 2^6=4^3
如果是奇数 先乘以1次底数再转换成偶数
例如 2^5=2*2^5
*/
int main(){
cin >> x >> p;
result = 1;
while (p>0){
if (p % 2 == 1)//奇数 先乘以1次底数
result = result * x;
p /= 2;//p除以2 向下取整 奇数 5/2=2...1 底数已经被乘到结果1次
x = x * x;//底数倍增 2变成2^2
}
cout <<result<< endl;
return 0;
}
从快速幂的实现算法可以看出,指数除2和二进制对应
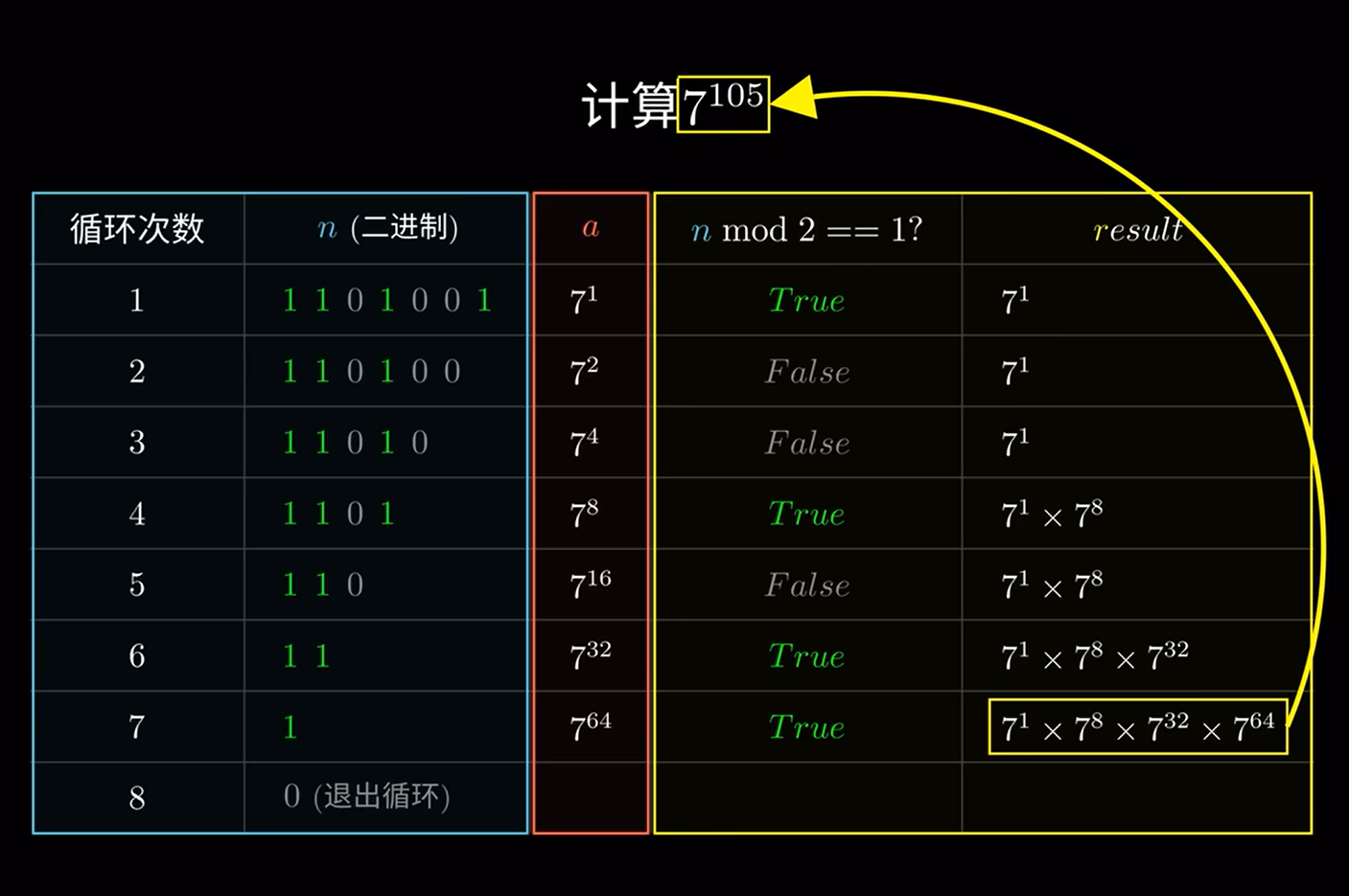
例如底数为7指数为105时,计算7^105,指数对应二进制
朴素算法需要循环105次,7*7*7...7为105个7相乘
快速幂
(105)=(1101001)2
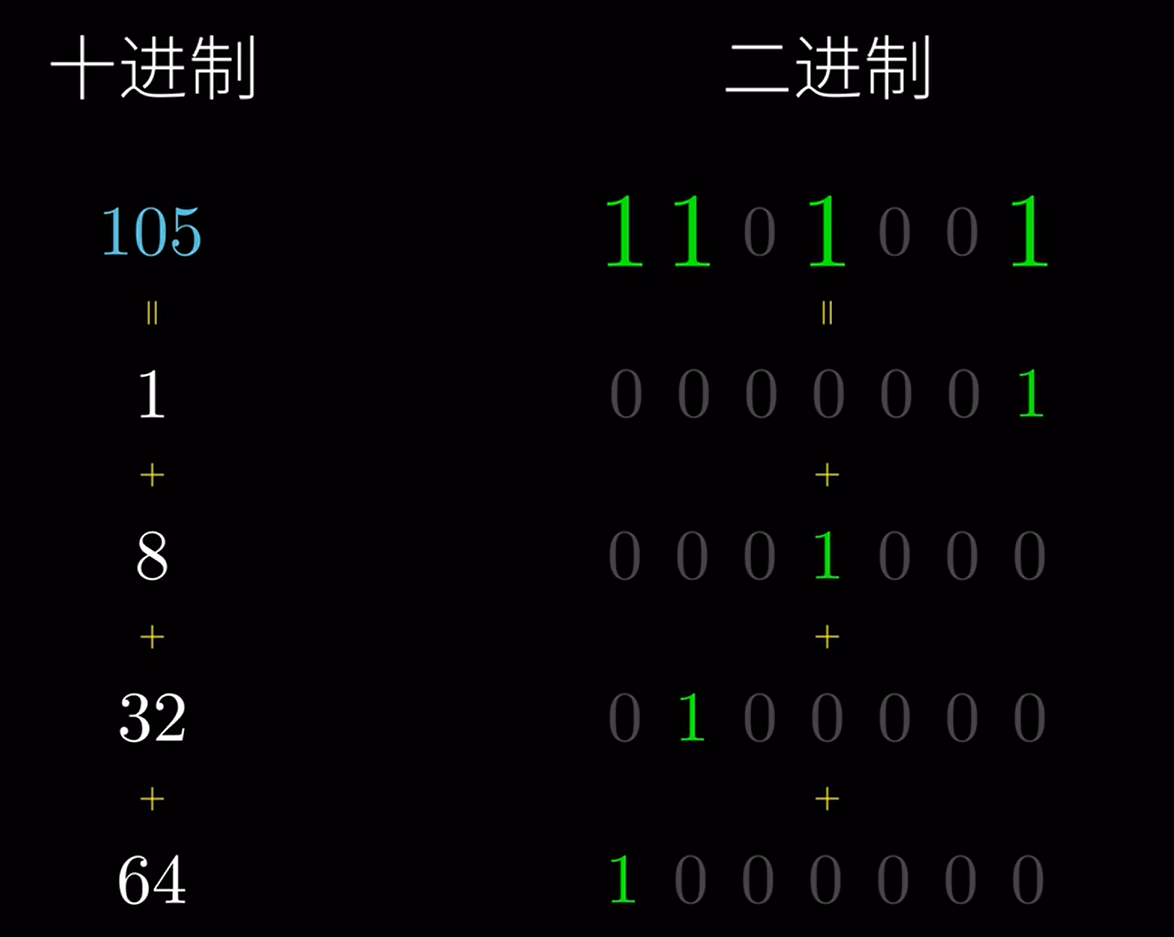
每次去除最右边的一位,需要7次可以完成,当对应二进制为1时,需要乘以当前底数
7^1*7^8*7^32*7^64
整数类型范围
| 数据类型 | 描述 | 取值范围 |
|---|---|---|
char |
字符型 | -128 到 127 或 0 到 255(取决于是否是有符号的) |
short |
短整型 | -32,768 到 32,767 |
int |
整型 | -2,147,483,648 到 2,147,483,647 |
long |
长整型 | -9,223,372,036,854,775,808 到 9,223,372,036,854,775,807 |
long long |
更长的整型 | -9,223,372,036,854,775,808 到 9,223,372,036,854,775,807 |
计算机表示整数的类型为long long 取值最大9,223,372,036,854,775,807,而7^105的值大于这个数,计算机处理时会溢出无法计算出正确结果
通常计算出这么大的数字也没有意义,我们实际情况通常使用模运算计算出其余数
3) 模运算
模运算,就是取余数,在计算机语言中用%来表示。举个简单的例子,3 % 5 = 3。结果的取值范围在 0 与模之间
例如
c=x/y
c=3 mod 5 =3 c的取值范围 [0,y-1]
结果也可以用负数表示,即 c=-2
4) 模运算性质
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p ) % p
(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p)^b) % p
5)模运算快速幂
(a * b) % p = (a % p * b % p) % p
根据上述模运算的乘法性质可知,每次循环的时候进行1次模运算,快速幂算法改造如下
#include<iostream>
using namespace std;
int x, p,i, result;
/*
快速幂
指数除以2,底数倍增是等价的
例如 2^4=4^2 2^6=4^3
如果是奇数 先乘以1次底数再转换成偶数
例如 2^5=2*2^5
*/
int main(){
cin >> x >> p>>m;//x的p次方对m取模
result = 1;
while (p>0){
if (p % 2 == 1)//奇数 先乘以1次底数
result = result * x % m;//每次乘以底数都进行取模
p /= 2;//p除以2 向下取整 奇数 5/2=2...1 底数已经被乘到结果1次
x = x * x % m;//底数倍增后取模 2变成2^2
}
cout <<result<< endl;
return 0;
}
3 思路分析
1 ①处应填( 1 )
分析
需要1个初始值开始乘,因此是1
正常初始值需要相乘时为1,需要累加是为0
06 result = ①;
2 ②处应填( p>0 或p!=0 或 p )
分析
快速幂的基本思想为把底数倍增累乘到结果,指数除以2,直到为0
因此p>0就继续循环指向
同时p除以2,一直到0为止,也可以是p!=0
布尔型变量和整形变量可以转换,0为false,非0为true,因此也可以填p,为0时条件为false退出循环
07 while (②){
3 ③处应填( result * x %m )
分析
为奇数时累加1次底数result * x,
另外结果需要对m取模,根据模运算性质(a * b) % p = (a % p * b % p) % p
可以每次单独取模
08 if (p % 2 == 1)
09 result = ③;
4 ④处应填( x * x %m )
分析
底数倍增 因此x=x * x
另外结果需要对m取模,根据模运算性质(a * b) % p = (a % p * b % p) % p
可以每次单独取模
11 x = ④;
5 ⑤处应填( result )
分析
result变量为快速幂结果,输出result即可
13 cout << ⑤ << endl;
作者:newcode 更多资源请关注纽扣编程微信公众号

从事机器人比赛、机器人等级考试、少儿scratch编程、信息学奥赛等研究学习



