信息学奥赛初赛天天练-66-NOIP2017普及组-基础题5-模运算、周期性规律、观察找规律

PDF文档公众号回复关键字:20240816

NOIP 2017 普及组 基础题5

21 一个人站在坐标 (0,0) 处，面朝 x 轴正方向。第一轮，他向前走 1 单位距离，然后右转；第二轮，他向前走 2 单位距离，然后右转；第三轮，他向前走 3 单位距离，然后右转……他一直这么走下去。请问第 2017 轮后，他的坐标是：( , )。（请在答题纸上用逗号隔开两空答案）

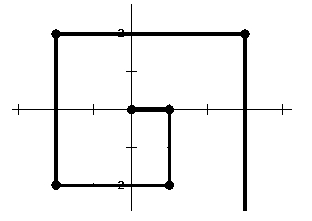
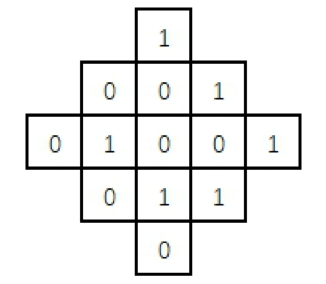
22 如下图所示，共有 13个格子。对任何一个格子进行一次操作，会使得它自己以及与它上下左右相邻的格子中的数字改变（由 1变 0，或由 0变 1）。现在要使得所有的格子中的数字都变为 0，至少需要( )次操作。

2 相关知识点

1) 模运算

模运算，就是取余数，在计算机语言中用%来表示。举个简单的例子，3 % 5 = 3。结果的取值范围在 0 与模之间

例如

c=x/y

c=3 mod 5 =3 c的取值范围 [0,y-1]

结果也可以用负数表示，即 c=-2

2) 周期性规律

周期性规律在数学中是一个重要的概念，它涉及到一系列按照固定模式重复出现的现象

周期性规律指的是某一现象或数列按照固定的时间间隔或模式重复出现的规律。例如，每天的日夜交替、每年的四季更迭、以及音乐中的旋律重复等

例如

2017 年 10 月 1 日是星期日，1999 年 10 月 1 日是( C )
A 星期三
B 星期日
C 星期五
D 星期二

分析

关键在于计算1999年10月1日到2017年10月1日之间的天数，然后根据星期的周期性确定1999年10月1日是星期几
1999~2007中有2007-1999=18年，其中2000，2004，2008，2012，2016这5年为闰年，其余为平年，平年一年365天，闰年比平年多1天，为366天
所以1999年10月1日~2017年10月1日共
18*365+5=6575天
由于每周是以7天一个周期
6575/7=939...2
所以从1999年10月1日到2017年10月1日，需要经过939周再加2天
因此1999年10月1日是礼拜五，经过939周变为2017年的礼拜五，再加2天为礼拜天

3 思路分析

21 一个人站在坐标 (0,0) 处，面朝 x 轴正方向。第一轮，他向前走 1 单位距离，然后右转；第二轮，他向前走 2 单位距离，然后右转；第三轮，他向前走 3 单位距离，然后右转……他一直这么走下去。请问第 2017 轮后，他的坐标是：( 1009 , 1008 )。（请在答题纸上用逗号隔开两空答案）

分析

每四轮移动后，坐标会回到原点附近的一个对称位置，并且方向会重置为面朝，x轴正方向。具体来说，每四轮移动形成的坐标变化可以看作是一个周期性的模式
从圆点0，0出发第1周期结束后
x轴方向，先向右移动1，然后向左移动3，所以左移2，为-2
y轴方向，先向下移动2，然后向上移动4，所以上移2，为2

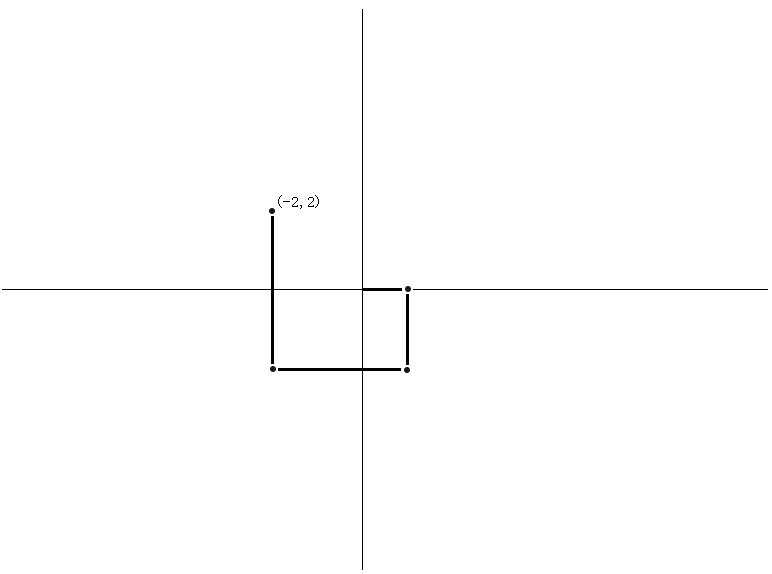
第2周期结束后
x轴方向，先向右移动5，然后向左移动7，所以左移2，为-4
y轴方向，先向下移动6，然后向上移动8，所以上移2，为4

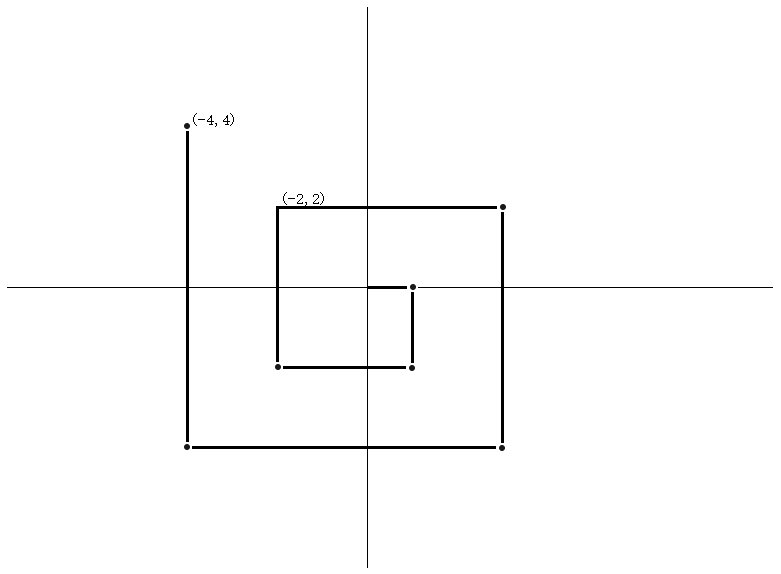
通过2个周期后，发现，每个周期为x轴左移2，y轴上移2
经过2017轮后，经过2017/4=504...1
经过了504个周期后，x左移504*2=1008，y上移504*2=1008，此时坐标为(-1008,1008)
此时还需要向右移动一次，第1轮移动1，第2轮移动2...第2017轮移动2017
x从-1008右移动2017，为2017-1008=1009
所以2017轮后的坐标为(1009,1008)

22 如下图所示，共有 13个格子。对任何一个格子进行一次操作，会使得它自己以及与它上下左右相邻的格子中的数字改变（由 1变 0，或由 0变 1）。现在要使得所有的格子中的数字都变为 0，至少需要( 3 )次操作。

分析

1 要想尽可能少的次数把格子中的1变成0，需要每次尽可能多的格子把1变成0或者可以创造条件让后面1次或者后面几次尽可能多的格子的1变成0
对如下绿色格子进行1次操作，绿色格子和相邻的橙色格子都进行变换，变换后结果如下

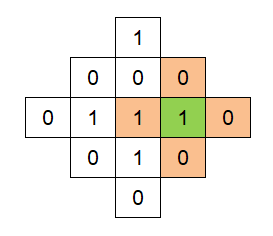
2 对如下绿色格子进行1次操作，绿色格子和相邻的橙色格子都进行变换，变换后结果如下
本次只有1个绿色格子和1个橙色格子进行变换，变换的格子不多，但为1次变换增加了1个格子，有利于下1次变换

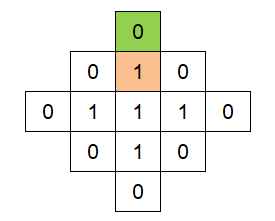
3 2 对如下绿色格子进行1次操作，绿色格子和相邻的橙色格子都进行变换，变换后结果如下
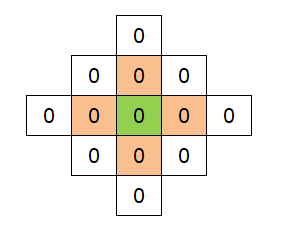
本次变换了绿色格子和周边的4个橙色格子，变换格子数最多，变换后所有格子都为0了
所以进行3次变换